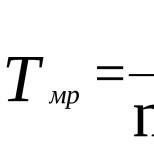Рабочая книга по математике. Обратные тригонометрические функции, их графики и формулы

Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.

Определение обратных тригонометрических функций

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y

Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .

Арктангенс (y = arctg x ) - это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .

Арккотангенс (y = arcctg x ) - это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x

arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x

Формулы, связывающие обратные тригонометрические функции

Формулы суммы и разности

при или

при и

при и

при

при

О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

III. Углы отрицательные. Углы, большие 360°.

§ 48. Обратные круговые функции.

Если мы имеем одно уравнение с двумя неизвестными, то из него можно определить любое неизвестное через другое. Например, если имеем; 2х + 3у = 6, то:

а) у = 2 - 2 / 3 х ; б) x = 3 - 3 / 2 y .

Первое уравнение дает выражение у в функции х . Второе, наоборот, дает выражение х в функции у . В общем все три уравнения выражают одну и ту же зависимость между переменными x и у , но только форма выражения этой зависимости разная; первое уравнение не решено ни относительно х , ни относительно у , в следующем за функцию принято у , за аргумент х ; в последнем за функцию принято х , за аргумент у .

Такие две функции, которые выражают одну и ту же зависимость между переменными х и у , но в одной за функцию принято у , а в другой за функцию принято х , называются взаимно-обратными . Любую из них можно принять за прямую; тогда другая будет обратная.

Примеры взаимнообратных функций:

у = 5х + 3; х = (у -3) / 5 ;

у = 2х ; х = 1 / 2 у

у = х 2 ; х = ±√ у ;

у = 3 √х ; х = у 3 .

Понятие обратности можно применить и к тригонометрическим функциям.

Например, мы употребляем равенство: y = sin x ; это значит, что у есть синус дуги х ; значит, обратно, х есть дуга, синус которой y . Точно так же: 1 / 2 = sin 30°, т. е. половина есть синус дуги в 30°. Наоборот, 30° есть дуга, синус которой равен половине.

Вместо того чтобы объяснять обратную зависимость словами, употребляют особый знак, обозначающий слово дуга: arc (читается „арк"; по-французски означает, дуга, арка).

Таким образом можно написать:

1 / 2 = sin 30°; 30° = arc sin 1 / 2 ;

1 / 2 = cos 60°; 60° = arc cos 1 / 2 ;

1= tg 45°; 45° = arc tg 1;

sin 16° = 0,276; 16° = arc sin 0,276;

cos π / 4 = 0,707; π / 4 = arc cos 0,707;

1= sin90°; 90° = arc sin 1;

1= cos 0°; 0° = arc cos 1;

1 = cos π; π = arc cos (-1);

tg π / 2 = ∞ ; π / 2 = arc tg ∞

sin π / 4 = cos π / 4 = 1 / 2 √2 ;

π / 4 = arc sin 1 / 2 √2 = arc cos 1 / 2 √2 .

На чертеже 37 дуга обозначена через х , ее синус черзз т , ее тангенс через р . Значит, х есть дуга, синус которой т , а тангенс р ; или:

х = arc sin т ; х = arc tg p .

Пользуясь тригонометрическими таблицами, мы решаем тоже две обратные задачи и пользуемся как прямыми, так и обратными тригонометрическими функциями. Если дана дуга (или угол), то мы отыскиваем тригонометрическую функцию: наоборот, если дана тригонометрическая функция и мы отыскиваем угол, то мы вычисляем значение обратной тригонометрической функции.

Из § 47 мы знаем, что одной и той же тригонометрической функции соответствует бесчисленное множество дуг, имеющих одно и то же начало; например, синусу, равному половине, соответствуют дуги: 30°, 150°, 390°, 510°,...; основные из них, 30° и 150°, имеют синус, равный половине, но если прибавить к каждой по 360°, то и новые дуги будут иметь тот же синус. Следовательно, обратные тригонометрические функции есть функции многозначные.

§ 49. В предыдущих примерах мы ограничивались наименьшей дугой, соответствующей данной тригонометрической функции, но можно было дать и общее выражение всех дуг, имеющих данный синус, косинус, тангенс. Если имеют в виду не наименьшее, а общее выражение всех дуг, имеющих данный синус, то обозначение дуги пишут с большой буквы; например:

arc sin 1 / 2 = 30°; но Arc sin 1 / 2 = 180° m + (- l) m 30°,

arc tg 1 = 45°, но Arc tg 1= 45° + 180° m .

Эти формулы взяты из § 47 (общий вид углов, соответствующих данному значению тригонометрической функции), но там еще не употреблялось обозначение обратной функции.

Если воспользоваться формулами § 47 и обобщить их, замени числовые значения буквенными, то получим следующую таблицу прямых и обратных тригонометрических функций:

y = sin x :; Arc sin y = m π + (- l) m x ;

y = cos x ; Arc cos y = 2m π ± x ;

y = tg x ; Arc tg y = m π + x ;

y = ctg x ; Arc ctg y = m π + x .

Большею частью, однако, по данной тригонометрической функции отыскивают наименьшую дугу (arc). При этом для положительных значений всех тригонометрических функций берут дугу в I четверти (от 0 до π / 2) ; для отрицательных значений синуса, тангенса, котангенса и косеканса берут дугу в I отрицательной четверти (от 0 до - π / 2) ; для отрицательного косинуса и секанса берут дугу во II четверти (от π / 2 до π).

Таким образом, для всех возможных значений синуса, тангенса, (котангенса) и косеканса дугу берут в пределах от - π / 2 до π / 2 , а для косинуса и секанса в пределах от 0 до π.

Обратные тригонометрические функции называются также обратными круговыми вследствие их связи с кругом.

Обрамтные тригонометримческие фумнкции (круговые функции , аркфункции ) - математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксимнус , арккомсинус , арктамнгенс , арккотангес. Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки "арк-" (от лат. arc - дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin ?1 для арксинуса и т.п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень?1. Основное соотношение

Функция y=arcsinX, её свойства и графики.

Арксинусом числа m называется такой угол x , для которогоФункция y = sinx y = arcsinx является строго возрастающей. (функция является нечётной).

Функция y=arccosX, её свойства и графики.

Арккосинусом числа m называется такой угол x , для которого

Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей. cos (arccosx ) = x при arccos (cosy ) = y при D (arccosx ) = [? 1; 1], (область определения), E (arccosx ) = . (область значений). Свойства функции arccos (функция центрально-симметрична относительно точки

Функция y=arctgX, её свойства и графики.

Арктангенсом числа m называется такой угол б, для которого Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arctg

Функция y=arcctg, её свойства и графики.

Арккотангенсом числа m называется такой угол x , для которого

Функция непрерывна и ограничена на всей своей числовой прямой.

Функция является строго убывающей. при при 0 < y < р Свойства функции arcctg (график функции центрально-симметричен относительно точки при любых x .

Простейшие тригонометрические уравнения.

Частные случаи тригонометрических уравнений

Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями.

Тригонометрические уравнения

Аксиомы стереометрии и следствия из них

Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

A и пересекаются по прямой а.

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Начальный уровень

Построение графика обратной зависимости (гиперболы). Визуальный гид (2019)

Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое обратная зависимость, и с чем ее едят. Если ты уверен, что знаешь все об обратной зависимости, добро пожаловать. Но если нет, тебе стоит прочитать тему « ».

Также очень советую научиться сперва строить , так как есть некоторые общие принципы для построения графика квадратичной и обратной зависимостей.

Начнем с небольшой проверки:

Что такое обратная пропорциональность?

Как выглядит функция, описывающая обратную зависимость в общем виде (формула)?

Как называется график такой функции?

Какие коэффициенты влияют на график функции, и как?

Если ты сходу смог ответить на эти вопросы, продолжай читать. Если хоть один вопрос вызвал затруднения, перейди по .

Итак, ты уже умеешь обращаться с обратной зависимостью, анализировать ее график и строить график по точкам.

Напоминаю: обратная зависимость в общем виде задается функцией

Давай вкратце вспомним, что делают коэффициенты.

Отвечает за «пологость» и направление графика: чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок). Знак коэффициента влияет на то, в каких четвертях расположен график: если, то ветви гиперболы расположены в и четвертях; если, то во и.

Дальше - число. Если внимательно посмотреть на знаменатель, видим, что - это такое число, которому не может равняться. То есть - это вертикальная асимптота , то есть вертикаль, к которой стремится график (на рисунке выше такой вертикалью является ось):

ОК, осталось еще одно число: . C ним все еще проще: если у нас уже есть гипербола (например, как на рисунке выше), а мы хотим гиперболу, то получается, что ордината каждой точки графика должны стать больше на, то есть нужно просто весь график сместить вверх на:

Как видим, теперь график стремится по горизонтали к прямой вместо оси, как было раньше. Такая прямая называется горизонтальной асимптотой .

Теперь давай научимся строить простейшую гиперболу - .

Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.

Например, построим гиперболу.

Составим таблицу из точек, которые принадлежат одной ветке (например, правой):

Отмечаем точки на рисунке:

Проводим через них плавную линию, которая краями приближается к осям:

Это одна ветвь гиперболы. Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат :

Отлично, осталось вспомнить, что собой представляет вторая ветвь? Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы. Вот:

Еще один полезный факт. Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны для правой ветви гиперболы, и для левой. Для функций, у которых - точный квадрат (например, или), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить. В этом случае достаточно даже трех точек, чтобы построить график.

Например, построим график функции. Как и в прошлый раз, начнем с правой ветви. Точка симметрии: . Выберем еще одну точку, например, . У третьей точки координаты будут наоборот: , . Рисуем:

И теперь симметрично отображаем эту ветвь в третью координатную четверть:

Теперь выясним, что будет, если? Очень просто: если есть график функции с таким же по величине, но положительным, то нужно просто отразить его относительно оси , то есть правая ветвь теперь будет ниже оси (в четверти), а левая - выше (в четверти). Принцип построения же останется прежним:

Ну что же, осталось объединить все то, что мы уже выяснили.

Итак, вот правило построения графика функции:

2) График должен быть сдвинут вправо на. Но проще двигать не график, а оси, так что ось сдвигаем влево на .

3) График должен быть сдвинут вверх на. Но проще двигать не график, а оси, так что ось сдвигаем вниз на .

Примеры:

Решения:

1. Пойдем по порядку по пунктам.

2. Сначала преобразуем выражение:

Теперь ясно, что; ; :

Дополнительное условие означает, что на графике появится выколотая точка c абсциссой:

5. . Ты уже, наверное, догадался, что вместо того, чтобы смотреть на эту функцию квадратными глазами и говорить «Что это??!!», нужно просто взять и упростить выражение. Если не знаешь, как это делать, то тебе прямая дорога в тему « ». Да-да, прямо сейчас, все бросай и переходи по ссылке!

Итак, если ты уже усвоил тему « », то тебе не составит труда упростить нашу функцию. Вот что должно получиться:

Выколотая точка:

6. . Здесь нужно не то чтобы упростить, тут нужно привести выражение к виду обратной зависимости. Мы такие штуки делали в теме « »:

Ну вот и все, ты научился строить любую гиперболу.

Замечу также, что правила построения гиперболы оказались немного проще, чем для параболы, ведь каждое число просто сдвигает график в какую-то одну сторону. И друг с другом коэффициенты не связаны.

ПОСТРОЕНИЕ ГРАФИКА ОБРАТНОЙ ЗАВИСИМОСТИ. КОРОТКО О ГЛАВНОМ

1. Определение

Функция, описывающая обратную зависимость - это функция вида, где.

График обратной зависимости - гипербола.

2. Коэффициенты, и.

Отвечает за «пологость» и направление графика : чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок). Знак коэффициента влияет на то, в каких четвертях расположен график:

если, и смещение вниз, если .
Следовательно, - это горизонтальная асимптота .

3. Правило построения графика функции:

0) Определяем коэффициенты, и.

1) Строим график функции (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).

2) График должен быть сдвинут вправо на. Но проще двигать не график, а оси, так что ось сдвигаем влево на .

3) График должен быть сдвинут вверх на. Но проще двигать не график, а оси, так что ось сдвигаем вниз на .

4) Старые оси (прямые, которые служили нам осями в пункте 1) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.