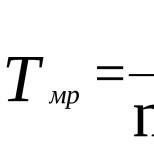Построение графика обратной зависимости (гиперболы). Визуальный гид (2019). Обратные тригонометрические функции, их свойства и графики. Построение графика обратной зависимости. коротко о главном

ОГЛАВЛЕНИЕ.

Глава I. О прогрессиях.
§ 1. Разностная прогрессия 3
§ 2. Вычисление любого члена разностной прогрессии по первому члену и разности 4
§ 3. Свойство членов разностной прогрессии, равноотстоящих от начала и от конца 5
§ 4. Вычисление суммы членов разностной прогрессии по первому члену последнему члену и числу членов -
§ 5. Вычисление суммы членов разностной прогрессии по первому члену разности прогрессии и числу членов 6
§ 6. Кратная прогрессия 11
§ 7. Вычисление любого члена кратной прогрессии по первому члену и знаменателю прогрессии 12
§ 8. Вычисление суммы членов кратной прогрессии по первому члену, поледнему и знаменателю прогрессии -

Глава II. Неравенства.
§ 9. Решение неравенства первой степени 18

Глава III. Основы учения о пределах.
§ 10. О математическом процессе изменения, о постоянных и переменных величинах в нем 23
§ 11. Понятие о величинах бесконечно малых и бесконечно больших. Понятие о пределе переменной величины 25
§ 12. Свойства бесконечно малых 29
§ 13. Основные положения о пределах 30
§ 14. Предельные результаты основных действий 32
§ 15. О десятичных периодических дробях 38
§ 16. Бесконечная кратная прогрессия. Вычисление предела суммы бесконечно убывающей кратной прогрессии 43

Глава IV. Иррациональные числа. Несоизмеримые величины.
§ 17. Понятие об иррациональном числе 49
§ 18. Сравнение иррациональных чисел 53
§ 19. Сложение, вычитание, умножение и деление иррациональных чисел 54
§ 20. Соизмеримые и несоизмеримые величины 57
§ 21 Способ нахождения общей наибольшей меры двух отрезков 57
§ 22. Пример несоизмеримости отрезков 59
§ 23. Отношение отрезков и вообще значений величины 60
§ 24. Понятие об измерении отрезков 61
§ 25. Пропорциональность величин -

Глава V. Правильные многоугольники. Длина окружности. Площадь круга.
§ 26. Определения 64
§ 27. Описанный и вписанный правильные многоугольники -
§ 28. Подобие правильных многоугольников и отношение их периметров 66
§ 29. Соотношения между радиусом круга и сторонами вписанных: квадрата, правильного шестиугольника, правильного треугольника и правильного десятиугольника 67
§ 30. Длина окружности 72
§ 31. Понятие о вычислении п 77
§ 32. Площади правильного многоугольника и круга 82
§ 33. Площадь сектора 84

Глава VI. Объемы призм и пирамид.
§ 34. Объем параллелепипеда 87
§ 35. Правило Кавальер и. Объем призмы 90
§ 36. Объем пирамиды 91
§ 37. Вспомогательные теоремы и замечания 98

Глава VII. Поверхности и объемы круглых тел.
§ 38. Общие сведения о цилиндре и конусе 107
§ 39. Поверхность цилиндра 109
§ 40. Поверхность конуса 110
§ 41. Объем цилиндра.. 111
§ 42. Объем конуса 112
§ 43. Тела вращения 113
§ 44. Теоремы Гюльдена 117
§ 45. Шар 118

Глава VIII. Гониометрия.
§ 46. Задачи гониометрии 126
§ 47. Угол и дуга, как переменные величины. Обобщение понятий дуги и угла -
§ 48. Радианное измерение дуг и углов 132
§ 49. Круговые функции. Синус и косинус угла и дуги 136
§ 50. Круговые функции. Тангенс и котангенс угла и дуги 14?
§ 51. Круговые функции отрицательного аргумента 144
§ 52. Круговые функции углов и дуг свыше 2 я. Периодичность круговых функций 146
§ 53. Графики круговых функций
§ 54. Зависимость между функциями дополнительных углов
§ 55. Приведение круговых функций к меньшему значению аргумента
§ 56. Понятие об обратных круговых функциях
§ 57. Синус, косинус и тангенс суммы и разности двух углов
§ 58. Синус, косинус и тангенс двойного угла и половины угла
§ 59. Основные формулы приведения тригонометрических выражений к виду удобному для логарифмирования
§ 60. Преобразования, приводящие к применению предыдущих формул
§ 61. Введение вспомогательного угла

Глава IX. Решение косоугольного треугольника.
§ 62 Основные соотношения между элементами косоугольного треугольника 172
§ 63 Вывод формул для определения тангенса половинного угла треугольника -
§ 64 Формулы для определения отношения суммы или разности двух сторон треугольника к третьей 175
§ 65 Теорема тангенсов 177
§ 66 Различные выражения площади треугольника 178
§ 67 Основные случаи решения косоугольного треугольника -
§ 68 Приложение формул косоугольного треугольника к различным вопросам 184

Глава X. Уравнения высших степеней, показательные, логарифмические и тригонометрические.
§ 69. Общие замечания о решении простейших уравнений высших степеней, сводящихся к уравнениям 1-й и 2-й степени 187
§ 70. Возвратные уравнения четвертой степени -
§ 71. Двучленные уравнения 189
§ 72. Трехчленные уравнения 192
§ 73. Решение систем уравнений 194
§ 74. Показательные уравнения 198
§ 75. Логарифмические уравнения 200
§ 76. Общие замечания о тригонометрических уравнениях 203
§ 77. Общие выражения обратных круговых функций 205
§ 78. Решение тригонометрических уравнений 209

Глава XI. Теория соединений. Бином Ньютона.
§ 79. Общие замечания о соединениях 214
§ 80. Размещения 215
§ 81. Перестановки 217
§ 82. Сочетания 218
§ 83. Некоторые свойства сочетаний 220
§ 84. Бииом Ньютона (для целого и положительного показателя) 222
§ 85.Формула общего члена бинома Ньютона 226
§ 86. Свойства коэфициентов бинома 228

Составлена в соответствии с программами Гуса 1927 г.
под РЕДАКЦИЕЙ А. М. ВОРОНЦА
Издание четвертое, стереотипное 41 - 60 тысяча
Научно-педагогической секцией Государственного ученого совета допущено для школ 11 ступени

О ПРОГРЕССИЯХ. § 1. Разностная прогрессия.
Разностной прогрессией называется ряд чисел, в котором каждое последующее число получается из предыдущего прибавлением к нему одного и того же числа, называемого разностью прогрессии.
Числа, составляющие прогрессию, называются ее членами.
Если разность положительна, прогрессия называется возрастающей, потому что по мере удаления от начала ряда члены его приобретают возрастающие численные значения. Если разность отрицательна, прогрессия будет убывающая, потому что численное значение членов по мере удаления от начала ряда убывает.
KOHEЦ ФPAГMEHTA УЧЕБНИКА

Обрамтные тригонометримческие фумнкции (круговые функции , аркфункции ) - математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксимнус , арккомсинус , арктамнгенс , арккотангес. Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки "арк-" (от лат. arc - дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin ?1 для арксинуса и т.п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень?1. Основное соотношение

Функция y=arcsinX, её свойства и графики.

Арксинусом числа m называется такой угол x , для которогоФункция y = sinx y = arcsinx является строго возрастающей. (функция является нечётной).

Функция y=arccosX, её свойства и графики.

Арккосинусом числа m называется такой угол x , для которого

Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей. cos (arccosx ) = x при arccos (cosy ) = y при D (arccosx ) = [? 1; 1], (область определения), E (arccosx ) = . (область значений). Свойства функции arccos (функция центрально-симметрична относительно точки

Функция y=arctgX, её свойства и графики.

Арктангенсом числа m называется такой угол б, для которого Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Свойства функции arctg

Функция y=arcctg, её свойства и графики.

Арккотангенсом числа m называется такой угол x , для которого

Функция непрерывна и ограничена на всей своей числовой прямой.

Функция является строго убывающей. при при 0 < y < р Свойства функции arcctg (график функции центрально-симметричен относительно точки при любых x .

Простейшие тригонометрические уравнения.

Частные случаи тригонометрических уравнений

Определение. Уравнения вада sin x = a; cos x = a; tg x = a; ctg x = a, где x - переменная, aR, называются простейшими тригонометрическими уравнениями.

Тригонометрические уравнения

Аксиомы стереометрии и следствия из них

Основные фигуры в пространстве: точки, прямые и плоскости. Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

A и пересекаются по прямой а.

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

III. Углы отрицательные. Углы, большие 360°.

§ 48. Обратные круговые функции.

Если мы имеем одно уравнение с двумя неизвестными, то из него можно определить любое неизвестное через другое. Например, если имеем; 2х + 3у = 6, то:

а) у = 2 - 2 / 3 х ; б) x = 3 - 3 / 2 y .

Первое уравнение дает выражение у в функции х . Второе, наоборот, дает выражение х в функции у . В общем все три уравнения выражают одну и ту же зависимость между переменными x и у , но только форма выражения этой зависимости разная; первое уравнение не решено ни относительно х , ни относительно у , в следующем за функцию принято у , за аргумент х ; в последнем за функцию принято х , за аргумент у .

Такие две функции, которые выражают одну и ту же зависимость между переменными х и у , но в одной за функцию принято у , а в другой за функцию принято х , называются взаимно-обратными . Любую из них можно принять за прямую; тогда другая будет обратная.

Примеры взаимнообратных функций:

у = 5х + 3; х = (у -3) / 5 ;

у = 2х ; х = 1 / 2 у

у = х 2 ; х = ±√ у ;

у = 3 √х ; х = у 3 .

Понятие обратности можно применить и к тригонометрическим функциям.

Например, мы употребляем равенство: y = sin x ; это значит, что у есть синус дуги х ; значит, обратно, х есть дуга, синус которой y . Точно так же: 1 / 2 = sin 30°, т. е. половина есть синус дуги в 30°. Наоборот, 30° есть дуга, синус которой равен половине.

Вместо того чтобы объяснять обратную зависимость словами, употребляют особый знак, обозначающий слово дуга: arc (читается „арк"; по-французски означает, дуга, арка).

Таким образом можно написать:

1 / 2 = sin 30°; 30° = arc sin 1 / 2 ;

1 / 2 = cos 60°; 60° = arc cos 1 / 2 ;

1= tg 45°; 45° = arc tg 1;

sin 16° = 0,276; 16° = arc sin 0,276;

cos π / 4 = 0,707; π / 4 = arc cos 0,707;

1= sin90°; 90° = arc sin 1;

1= cos 0°; 0° = arc cos 1;

1 = cos π; π = arc cos (-1);

tg π / 2 = ∞ ; π / 2 = arc tg ∞

sin π / 4 = cos π / 4 = 1 / 2 √2 ;

π / 4 = arc sin 1 / 2 √2 = arc cos 1 / 2 √2 .

На чертеже 37 дуга обозначена через х , ее синус черзз т , ее тангенс через р . Значит, х есть дуга, синус которой т , а тангенс р ; или:

х = arc sin т ; х = arc tg p .

Пользуясь тригонометрическими таблицами, мы решаем тоже две обратные задачи и пользуемся как прямыми, так и обратными тригонометрическими функциями. Если дана дуга (или угол), то мы отыскиваем тригонометрическую функцию: наоборот, если дана тригонометрическая функция и мы отыскиваем угол, то мы вычисляем значение обратной тригонометрической функции.

Из § 47 мы знаем, что одной и той же тригонометрической функции соответствует бесчисленное множество дуг, имеющих одно и то же начало; например, синусу, равному половине, соответствуют дуги: 30°, 150°, 390°, 510°,...; основные из них, 30° и 150°, имеют синус, равный половине, но если прибавить к каждой по 360°, то и новые дуги будут иметь тот же синус. Следовательно, обратные тригонометрические функции есть функции многозначные.

§ 49. В предыдущих примерах мы ограничивались наименьшей дугой, соответствующей данной тригонометрической функции, но можно было дать и общее выражение всех дуг, имеющих данный синус, косинус, тангенс. Если имеют в виду не наименьшее, а общее выражение всех дуг, имеющих данный синус, то обозначение дуги пишут с большой буквы; например:

arc sin 1 / 2 = 30°; но Arc sin 1 / 2 = 180° m + (- l) m 30°,

arc tg 1 = 45°, но Arc tg 1= 45° + 180° m .

Эти формулы взяты из § 47 (общий вид углов, соответствующих данному значению тригонометрической функции), но там еще не употреблялось обозначение обратной функции.

Если воспользоваться формулами § 47 и обобщить их, замени числовые значения буквенными, то получим следующую таблицу прямых и обратных тригонометрических функций:

y = sin x :; Arc sin y = m π + (- l) m x ;

y = cos x ; Arc cos y = 2m π ± x ;

y = tg x ; Arc tg y = m π + x ;

y = ctg x ; Arc ctg y = m π + x .

Большею частью, однако, по данной тригонометрической функции отыскивают наименьшую дугу (arc). При этом для положительных значений всех тригонометрических функций берут дугу в I четверти (от 0 до π / 2) ; для отрицательных значений синуса, тангенса, котангенса и косеканса берут дугу в I отрицательной четверти (от 0 до - π / 2) ; для отрицательного косинуса и секанса берут дугу во II четверти (от π / 2 до π).

Таким образом, для всех возможных значений синуса, тангенса, (котангенса) и косеканса дугу берут в пределах от - π / 2 до π / 2 , а для косинуса и секанса в пределах от 0 до π.

Обратные тригонометрические функции называются также обратными круговыми вследствие их связи с кругом.

Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.

Определение обратных тригонометрических функций

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y

Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .

Арктангенс (y = arctg x ) - это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .

Арккотангенс (y = arcctg x ) - это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin x

y = arccos x