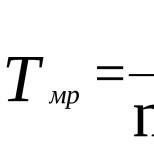Простейшие системы массового обслуживания и их параметры. по дисциплине «Математические методы»

Через эти вероятности выражается среднее число занятых каналов

=P 1 + 2P 2 +…+n(P n +P n+ 1 +…+P s ) или

=P 1 + 2P 2 +…+(n- 1)P n- 1 +n(1-P 0 -P 1 -…-P n-1 ).

Через находим абсолютную пропускную способность системы:

а также среднее число заявок в системе

М =s- =s- .

Пример 1 . На вход трехканальной СМО с отказами поступает поток заявок с интенсивностью =4 заявки в минуту, время обслуживания заявки одним каналом t обсл =1/? =0,5 мин. Выгодно ли с точки зрения пропускной способности СМО заставить все три канала обслуживать заявки сразу, причем среднее время обслуживания уменьшается втрое? Как это скажется на среднем времени пребывания заявки в СМО?

Решение. Находим вероятность простоя трехканальной СМО по формуле

? =/? =4/2=2, n=3,

Р 0 = = = 0,158.

Вероятность отказа определяем по формуле:

Р отк =Р n = =

P отк = 0,21.

Относительная пропускная способность системы:

Р обсл = 1-Р отк 1-0,21=0,79.

Абсолютная пропускная способность системы:

А= Р обсл 3,16.

Среднее число занятых каналов определяем по формуле:

1,58, доля каналов, занятых обслуживанием,

Cреднее время пребывания заявки в СМО находим как вероятность того, что заявка принимается к обслуживанию, умноженную на среднее время обслуживания: t СМО 0,395 мин.

Объединяя все три канала в один, получаем одноканальную систему с параметрами ?= 6, ?= 2/3. Для одноканальной системы вероятность простоя:

Р 0 = = =0,6,

вероятность отказа:

Р отк =? Р 0 = =0,4,

относительная пропускная способность:

Р обсл = 1-Р отк =0,6,

абсолютная пропускная способность:

А= Р обсл =2,4.

t СМО =Р обсл = =0,1 мин.

В результате объединения каналов в один пропускная способность системы снизилась, так как увеличилась вероятность отказа. Среднее время пребывания заявки в системе уменьшилось.

Пример 2 . На вход трехканальной СМО с неограниченной очередью поступает поток заявок с интенсивностью =4 заявки в час, среднее время обслуживания одной заявки t =1/?=0,5 ч. Найти показатели эффективности работы системы.

Для рассматриваемой системы n =3, =4, ?=1/0,5=2, ?= /?=2, ?/n =2/3<1. Определяем вероятность простоя по формуле:

P 0 = =1/9.

Среднее число заявок в очереди находим по формуле:

Среднее время ожидания заявки в очереди считаем по формуле:

t = = 0,22 ч.

Среднее время пребывания заявки в системе:

Т=t+ 0,22+0,5=0,72.

Пример 3 . В парикмахерской работают 3 мастера, а в зале ожидания расположены 3 стула. Поток клиентов имеет интенсивность =12 клиентов в час. Среднее время обслуживания t обсл =20 мин. Определить относительную и абсолютную пропускную способность системы, среднее число занятых кресел, среднюю длину очереди, среднее время, которое клиент проводит в парикмахерской.

Для данной задачи n =3, m =3, =12, ? =3, ? =4, ?/n =4/3. Вероятность простоя определяем по формуле:

P 0 = 0,012.

Вероятность отказа в обслуживании определяем по формуле

Р отк =Р n+m = .

P отк =P n+m 0,307.

Относительная пропускная способность системы, т.е. вероятность обслуживания:

P обсл =1-P отк 1-0,307=0,693.

Абсолютная пропускная способность:

А= Р обсл 12 .

Среднее число занятых каналов:

Средняя длина очереди определяется по формуле:

L= 1,56.

Среднее время ожидания обслуживания в очереди:

Среднее число заявок в СМО:

Среднее время пребывания заявки в СМО:

Т=М/ 0,36 ч.

Пример 4 . Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью =0,5 отказа в час, среднее время ремонта t рем =1/?=0,8 ч. Определить пропускную способность системы.

Эта задача рассматривает замкнутую СМО, ? =1,25, ?=0,5/1,25=0,4. Вероятность простоя рабочего определяем по формуле:

Вероятность занятости рабочего Р зан = 1-Р 0 . А=(1-P 0 )? =0,85? станков в час.

Решение задачи

Два рабочих обслуживают группу из четырех станков. Остановки работающего станка происходят в среднем через 30 мин. Среднее время наладки составляет 15 мин. Время работы и время наладки распределено по экспоненциальному закону.

Найдите среднюю долю свободного времени для каждого рабочего и среднее время работы станка.

Найдите те же характеристики для системы, в которой:

а) за каждым рабочим закреплены два станка;

б) два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью;

в) единственный неисправный станок обслуживают оба рабочих сразу (с двойной интенсивностью), а при появлении еще хотя бы одного неисправного станка они начинают работать порознь, причем каждый обслуживает один станок (вначале опишите систему в терминах процессов гибели и рождения).

Возможны следующие состояния системы S:

S 0 - все станки исправны;

S 1 - 1 станок ремонтируется, остальные исправны;

S 2 - 2 станок ремонтируется, остальные исправны;

S 3 - 3 станок ремонтируется, остальные исправны;

S 4 - 4 станок ремонтируется, остальные исправны;

S 5 - (1, 2) станки ремонтируются, остальные исправны;

S 6 - (1, 3) станки ремонтируются, остальные исправны;

S 7 - (1, 4) станки ремонтируются, остальные исправны;

S 8 - (2, 3) станки ремонтируются, остальные исправны;

S 9 - (2, 4) станки ремонтируются, остальные исправны;

S 10 - (3, 4) станки ремонтируются, остальные исправны;

S 11 - (1, 2, 3) станки ремонтируются, 4 станок исправен;

S 12 - (1, 2, 4) станки ремонтируются, 3 станок исправен;

S 13 - (1, 3, 4) станки ремонтируются, 2 станок исправен;

S 14 - (2, 3, 4) станки ремонтируются, 1 станок исправен;

S 15 - все станки ремонтируются.

Граф состояний системы…

Данная система S является примером замкнутой системы, так как каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта - в самой системе. Каждый рабочий является каналом обслуживания.

Если рабочий занят, он налаживает?-станков в единицу времени, пропускная способность системы:

Средняя доля свободного времени для каждого рабочего? 0,09.

Среднее время работы станка? 3,64.

а) За каждым рабочим закреплены два станка.

Вероятность простоя рабочего определяется по формуле:

Вероятность занятости рабочего:

Если рабочий занят, он налаживает?-станков в единицу времени, пропускная способность системы:

Средняя доля свободного времени для каждого рабочего? 0,62.

Среднее время работы станка? 1,52.

б) Два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью.

в) Единственный неисправный станок обслуживают оба рабочих сразу (с двойной интенсивностью), а при появлении еще хотя бы одного неисправного станка они начинают работать порознь, причем каждый обслуживает один станок (вначале опишите систему в терминах процессов гибели и рождения).

Сравнение 5 ответов:

Наиболее эффективным способом организации рабочих за станками будет являться начальный вариант задачи.

До сих пор мы рассматривали системы, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми . В некоторых же случаях обслуженные требования после задержки опять поступают на вход. Такие СМО называются замкнутыми .

· Поликлиника, обслуживающая данную территорию.

· Бригада рабочих, закрепленная за группой станков.

В замкнутых СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки .

В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта – в самой системе. Каждый работник является каналом обслуживания.

Пусть n – число каналов обслуживания, s – число потенциальных заявок, λ –интенсивность потока заявок каждого потенциального требования, m – интенсивность обслуживания, . Поток

· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):

(27)

· Финальные вероятности состояний системы

(28)

Через эти вероятности выражается среднее число замкнутых каналов :

Через находим абсолютную пропускную способность системы

а также среднее число заявок в системе

(31)

Пример решения задачи.

Рабочий обслуживает 4 станка. Каждый станок отказывает с интенсивностью λ = 0,5 отказа в час. Среднее время ремонта ч. Определить пропускную способность системы.

Решение

Эта задача рассматривает замкнутую СМО,

Вероятность простоя рабочего определяется по формуле (27):

Вероятность занятости рабочего

.

Если рабочий занят, он налаживает станков в единицу времени, пропускная способность системы

Станков в час.

Ø Важно помнить. При применении экономического показателя важно правильно оценить реальные издержки, которые могут изменяться, например, от времени года, от объема запасов угля и пр.

На практике часто встречаются; замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник «блокируется» на время обслуживания его заявки (т.е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значения интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.

Задание к работе:

1. Станция «Железная дорога» в мегаполисе принимает составы для разгрузки угля на платформах. В среднем за сутки на станцию прибывают 16 составов с углем. Поступление носит случайный характер. Плотность прихода составов показала, что поступление на разгрузку удовлетворяет пуассоновскому потоку с параметром состава в час. Время разгрузки состава является случайной величиной, удовлетворяющей экспоненциальному закону со средним временем разгрузки час. Простой состава в сутки составляет y.e; простой платформы в сутки за опоздание прихода состава – y.e; стоимость эксплуатации платформы в сутки – y.e. Издержки подсчитать за сутки. Требуется провести анализ эффективности функционирования станции.

2. Интернет-провайдер в небольшом городе имеет 5 выделенных каналов обслуживания. В среднем на обслуживание одного клиента уходит 25 минут. В систему в среднем поступает 6 заказов в час. Если свободных каналов нет, следует отказ. Определить характеристики обслуживания: вероятность отказа, среднее число занятых обслуживанием линий связи, абсолютную и относительную пропускные способности, вероятность обслуживания. Найти число выделенных каналов, при котором относительная пропускная способность системы будет не менее 0,95. Считать, что потоки заявок и обслуживаний простейшие.

3. Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. В предположении неограниченности очереди определить показатели эффективности работы причала и вероятность ожидания разгрузки не более 2 судов.

4. Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. Определить показатели работы порта при условии, что судно покидает порт при наличии в очереди более 3 судов.

Порядок выполнения работы:

1. Изучить инструкцию к практической работе.

2. Выполнить задание.

3. Оформить отчет.

3. Задачи.

4. Материальное обеспечение.

5. Практическое задание.

Вопросы для самоконтроля:

1. Дайте определение системы массового обслуживания с отказами.

2. Определите процесс функционирования системы массового обслуживания с отказами.

3. Перечислите основные характеристики системы массового обслуживания с отказами.

4. Дайте определение системы массового обслуживания с ограниченной очередью.

5. Определите процесс функционирования системы массового обслуживания с ограниченной очередью.

6. Перечислите основные характеристики системы массового обслуживания с ограниченной очередью.

7. В чем особенности замкнутых систем массового обслуживания?

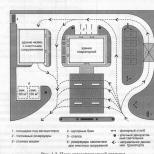
Пример. С1, С2, С3 – станки; НЦ – центральный накопитель; B – манипулятор. Транспортная тележка (манипулятор) транспортирует отработанную деталь от станка к накопителю и укладывает ее там, забирает новую деталь (заготовку), транспортирует ее к станку и устанавливает в рабочую позицию для зажима. Во время всего периода, необходимого для выгрузки–загрузки, станок простаивает. Время T з смены заготовки и есть время обслуживания.

Интенсивность обслуживания станков определяется как ,– среднее время обслуживания станка, которое вычисляется как, гдеn – число заявок. Интенсивность подачи станком заявки на обслуживание определяется как (где– среднеее время обработки детали станком).

Станочная система с однозахватным манипулятором представляет собой СМО с ожиданием с внутренней организацией FIFO: каждая заявка станка на обслуживание удовлетворяется, в случае когда манипулятор занят, заявка становится в очередь и станок ожидает когда манипулятор освободится. Данный процесс марковский, т.е. случайная выдача заявки на обслуживание в определенный момент времени t 0 не зависит от предыдущих заявок, т.е. от течения процесса в предшествующий период. Продолжительность исполнения заявки может быть различной и является случайной величиной, не зависящей от числа поданных заявок. Весь процесс не зависит от того, что произошло ранее момента времени t 0 .

В станочной системе число заявок на обслуживание может быть равно 0, 1, 2, ... m , где m – общее число станков. Тогда возможны следующие состояния:

S 0 – все станки работают, манипулятор стоит.

S 1 – все станки, кроме одного, работают, манипулятор обслуживает станок, от которого поступила заявка на смену заготовок.

S 2 – работают m -2 станка, на одном станке идет смена заготовки, другой ожидает.

S 3 – работают m -2 станка, один станок обслуживается манипулятором, два станка ожидают в очереди.

S m – все станки стоят, один обслуживается манипулятором, остальные ожидают очереди исполнения заказа.

Рис.4.6.

Вероятность перехода в состояние S k из одного из возможных состояний S 1 , S 2 , ... S m зависит от случайного поступления заявок на обслуживание и вычисляется как:

p 0 – вероятность того, что все станки работают.

Манипулятор работает при состояниях системы от S 1 до S m ­ . Тогда вероятность его загрузки равна: .

Число станков, находящихся в очереди связано с состояниями S 2 , – S m , при этом один станок обслуживается, а (k-1) – ожидают. Тогда, среднее число станков в очереди: .

Коэффициент простоя одного станка (из-за ожидания при многостаночном обслуживании): .

Среднее использование одного станка:

Применение метода Монте-Карло для решения задач, связанных с теорией массового обслуживания

Для того, чтобы описать поток однородных событий, достаточно знать закон распределения моментов времени t 1 , t 2 , ..., t k , ..., в которые поступают события.

Для удобства дальнейших рассмотрений целесообразно от величин t 1 , t 2 , ..., перейти к случайным величинам  1 ,  2 , ...,  m , ... , таким образом, что:

Случайные величины  k являются длинами интервалов времени между последовательными моментами t k .

Совокупность случайных величин  i считается заданной, если определена совместная функция распределения: . Обычно рассматриваются только непрерывные случайные величины k , поэтому часто пользуются соответствующей функцией плотности f (z 1 , z 2 ,..., z k ) .

Обычно в теории СМО рассматриваются потоки однородных событий без последействия, для которых случайные величины  k независимы. Поэтому . Функцииf i (z i ) при i >1 представляют собой условные функции плотности при условии, что в начальный момент интервала  k (i >1) поступила заявка. В отличие от этого функция f 1 (z 1 ) является безусловной функцией плотности, т.к. относительно появления или непоявления заявки в начальный момент времени не делается никаких предположений.

Широкое применение имеют так называемые стационарные потоки, для которых вероятностный режим их во времени не изменяется (т.е. вероятность появления k заявок за промежуток времени (t 0 , t 0 + t ) не зависит от t 0 , а зависит только от t и k ). Для стационарных потоков без последействия имеют место соотношения:

где  – плотность стационарного потока.

Поступившая в систему заявка может занимать только свободные линии. Относительно порядка занятия линий могут быть сделаны различные предположения:

а) линии занимаются в порядке их номеров. Линия с большим номером не может быть привлечена к обслуживанию заявки, если имеется свободная линии с меньшим номером;

б) линии занимаются в порядке очереди. Освободившаяся линия поступает в очередь и не начинает обслуживания заявок до израсходования всех ранее освободившихся линий;

в) линии занимаются в случайном порядке в соответствии с заданными вероятностями. Если в момент поступления очередной заявки имеется n св свободных линий, то в простейшем случае вероятность занять некоторую определенную линию может быть принята равной . В более сложных случаях вероятности считаются зависящими от номеров линий, моментов их освобождения и других параметров.

Аналогичные предположения можно сделать и относительно порядка принятия заявок к обслуживанию в том случае, когда в системе образуется очередь заявок:

а) заявки принимаются к обслуживанию в порядке очереди. Освободившаяся линия приступает к обслуживанию той заявки, которая ранее другой поступила в систему;

б) заявки принимаются к обслуживанию по минимальному времени получения отказа. Освободившаяся линия приступает к обслуживанию той заявки, которая в кратчайшее время может получить отказ;

в) заявки принимаются к обслуживанию в случайном порядке в соответствии с заданными вероятностями. Если в момент освобождения линии имеется m заявок в очереди, то в простейшем случае вероятность выбрать для обслуживания некоторую определенную заявку может быть принята равной q =1/ m . В более сложных случаях вероятности q 1 , q 2 ,..., q m считаются зависящими от времени пребывания заявки в системе, времени, остающегося до получения отказа и других параметров.

Для решения ряда прикладных задач оказывается необходимым учитывать такой важный фактор, как надежность элементов обслуживающей системы. Будем предполагать, что с точки зрения надежности каждая линия в данный момент времени может быть либо исправной, либо неисправной. Надежность линии определяется вероятностью безотказной работы R = R (t ) , задаваемой как функция времени. Будем также предполагать, что линия, вышедшая из строя по причине неполной надежности, может быть введена в строй (отремонтирована), для чего требуется затратить время p . Величину p будем считать случайной величиной с заданным законом распределения.

Относительно судьбы заявки, при обслуживании которой линия выходит из строя, могут быть сделаны различные предположения: заявка получает отказ; заявка остается в системе (с общим временем пребывания в системе не более  n ) как претендент на обслуживание вне очереди; заявка поступает в очередь и обслуживается на общих основаниях и т.д.

Сущность метода статистических испытаний применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы, при помощи которых можно вырабатывать случайные реализации заданных потоков однородных событий, а также «моделировать» процессы функционирования обслуживающих систем. Эти алгоритмы используются для многократного воспроизведения реализаций случайного процесса обслуживания при фиксированных условиях задачи. Получаемая при этом информация о состояниях процесса подвергается статистической обработке с целью оценки, являющихся показателями качества обслуживания.

Метод статистических испытаний позволяет более полно, по сравнению с асимптотическими формулами, исследовать зависимость качества обслуживания от характеристик потока заявок и параметров обслуживающей системы.

Это достигается благодаря двум обстоятельствам. Во-первых, при решении задач теории массового обслуживания методом статистических испытаний может быть использована более обширная информация о процессе, чем это обычно удается сделать, применяя аналитические методы.

С другой стороны, значения показателей качества обслуживания, получаемые из асимптотических формул, строго говоря, относятся к моментам времени, достаточно удаленным от начала процесса. Реально, для моментов времени, близких к началу процесса, когда еще не наступил стационарный режим, значения показателей качества обслуживания в общем случае существенно отличаются от асимптотических значений. Метод статистических испытаний позволяет достаточно обстоятельно изучать переходные режимы.

Для многих прикладных задач предположения, при которых справедливы аналитические формулы, оказываются слишком стеснительными. При решении задач методом статистических испытаний некоторые предположения могут быть существенно ослаблены.

В первую очередь это относится к многофазному обслуживанию (т.е. рассматриваются обслуживающие системы, состоящие из нескольких последовательно действующих в общем случае неоднотипных агрегатов).

Другим важным обобщением задачи является предположение о характере потока заявок, поступающих на обслуживание. Допускается рассмотрение потоков однородных событий с практически произвольным законом распределения. Последнее обстоятельство оказывается существенным по следующим двум причинам. Во-первых, реальные потоки заявок в некоторых случаях заметно отличаются от простейшего. Для пояснения второй причины предположим, что исходный поток заявок достаточно точно аппроксимируется простейшим потоком. При этом поток заявок, обслуженных на первой фазе, уже, строго говоря не будет простейшим. Поскольку поток, являющийся выходным для первой фазы, будет входным потоком для агрегата, обслуживающего заявки на второй фазе, мы снова приходим к задаче обслуживания потоков, не являющимися простейшими.