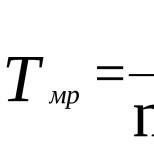Оценка средней арифметической. Определение среднего значения, вариации и формы распределения. Описательные статистики. Ловушки, связанные с описательными статистиками
То, какие величины можно применять для оценки средних параметров, а какие нельзя, зависит от типа шкалы. В самом деле, среднее арифметическое значение пола вряд ли будет иметь смысл. Тем не менее, оценить средние параметры имеет смысл для любой шкалы. Оценку средних параметров еще называют измерением центральной тенденции . Эта задача, наряду с оценкой разброса значений, входит в раздел описательной статистики и является одним из первых шагов при обработке социологического опроса.
При номинальной шкале измерения мы можем лишь указать наиболее популярный ответ. Наиболее популярный ответ называется модой . Моду можно вычислить и при любой шкале. Однако это будет иметь смысл делать только тогда, когда число опрошенных значительно больше, чем число вариантов ответов. Действительно, если например, измерять рост в миллиметрах, то у всех 100-200 опрошенных окажутся разные значения роста. Модами тогда окажутся все эти варианты (они же будут максимально популярными!).
Имейте в виду, что мода – это вариант ответа, а не число человек, которые выбрали этот вариант. Также имейте в виду, что мод может быть несколько (как в предыдущем примере).
Если шкала порядковая , то помимо моды можно вычислить также медиану . Поясним смысл медианы. При порядковой шкале все варианты ответов можно расположить в порядке возрастания некоторого признака. Если это сделать, то какой-то ответ окажется в середине этого списка. Этот ответ и будет медианой. Другими словами, медиана – это ответ, стоящий в середине упорядоченной выборки. Медиана – это вариант ответа, а не то, сколько раз этот ответ встречается в выборке. Медиану можно вычислить и при интервальных шкалах, поскольку эти шкалы также позволяют расположить ответы в порядке возрастания. Для номинальной шкалы вычислить медиану нельзя! О способах вычисления медианы будет более подробно рассказано ниже на примерах.
Для интервальных (метрических) шкал оценкой средних параметров является среднее арифметическое значение . Оно равно сумме всех значений, деленной на число этих значений:
Среднее арифметическое более точно отражает средние параметры выборки, чем медиана, поскольку медиана не учитывает величины отклонений отдельных измерений от средних показателей. Ни для порядковой шкалы, ни для номинальной шкалы среднее арифметическое значение вычислить нельзя. Ведь сумма значений для этих шкал не имеет смысла, даже если ее можно формально вычислить, просуммировав коды ответов.
Для дихотомической шкалы в качестве меры средней тенденции возможно использовать только моду – какой из ответов более популярен.
Оценка средней величины имеет целью установить величину генеральной средней для изученной категории объектов. Требуемая для этой цели ошибка репрезентативности определяется по формуле:
При изучении шерстной продуктивности одной породы овец было взято из разных мест обитания породы у 100 взрослых овец 100 годовых настригов шерсти. Средний настриг у 100 овец оказался μ = 5,0 кг, стандартное отклонение для этой выборки s = 1,0. Ответственность исследования обычная, поэтому был принят первый порог вероятности безошибочных прогнозов b 1 = 0,95.
Оценка среднего настрига для всей породы может быть проведена следующим образом:
n = 100; μ = 5,0; s = 1,0; n = 100 – 1 = 99; t = 2,0;

D = 2,0 × 0,1 =0,2;
μ max =5,0 + 0,2 = 5,2 (возможный максимум);
μ min = 5,0 – 0,2 = 4,8 (гарантированный минимум).
1 Средний настриг шерсти по изученной выборке равен
μ ± = 5,0 ± 0,2, доверительные границы генеральной средней 4,8 – 5,2. По этим показателям можно провести сравнение результатов проведенного исследования с результатами других работ.
2 Планировать выход шерсти (n = 10000) на основе проведенного исследования следует исходя из гарантированного минимума генеральной средней μ min = 4,8 кг на одну голову, или 48 т шерсти от всех взрослых овец породы.
3 Работы по стрижке, обработке, перевозке и хранению шерсти следует планировать исходя из возможного максимума генеральной средней μ mах = 5,2 кг с головы, или 52 т от всех овец изученной категории.
При изучении способности к обучению белых мышей для каждой из 40 особей определенного происхождения регистрировалось время прохождения лабиринта в поисках корма после пятой попытки В одном опыте были получены следующие сводные показатели:
n = 40, μ = 7,0 мин, s = 3,0 мин
Требовалось определить возможное время прохождения лабиринта в среднем для мышей всей изучаемой линии, что можно сделать следующим образом: n = 40, μ = 7,0, s = 3,0, n = 40 – 1 = 39, t = 2 (ответственность обычная: b = 0,95), = 3 / = 0,48; D = 2 × 0,48 = 0,96 ≈ 1,0, т.е не более 7,0 + 1,0 = 8,0; не менее 7,0 – 1,0 = 6,0.
1 Среднее время для опытной группы
μ ± = 7,0 ± 0,48 мин.
2 Доверительные границы генеральной средней
μ ± D = 6,0 – 8,0 мин.
3 Если встретится группа мышей со средним временем или меньше 6 мин. или больше 8 мин., возникнет предположение, что эта группа отличается от изученной по способности проходить лабиринт. Это предположение необходимо будет проверить методом определения достоверности разности.
Оценка средней разности
В некоторых исследованиях в качестве первичных данных берется разность двух измерений. Это может быть в случае, когда каждая особь выборки изучается в двух состояниях – или в разном возрасте, или при разных условиях жизни. В этих случаях индивидуальные и средние разности по своему знаку и величине могут характеризовать действие на изучаемый признак или возраста, или изменения условий жизни.
Характеристика действия определенных факторов по разности может быть произведена также и в экспериментах с аналогами, когда каждой особи в опытной группе соответствует строго определенная особь в контроле
При сортоиспытании пшеницы новый сорт А сравнивался со стандартным сортом В по разности урожаев, полученных на 20 парах параллельных делянок: d i = A i – В i . В результате в качестве первичных материалов было получено 20 разностей, некоторые из них были положительными (A>В), некоторые – отрицательными (А<В).
Для всей выборки, состоящей из 20 разностей, были получены сводные выборочные показатели: n = 20, μ = + 1,0 ц/га, s = 2,5 ц/га. В этой выборке новый сорт оказался лучше стандартного: А – В= + 1,0; A>В.
Возник вопрос: а будет ли и весь новый сорт (а не только выборка из него) в аналогичных условиях лучше стандартного? Можно ли считать, что полученная средняя выборочная положительная разность d =+1,0 правильно отражает соответствующую генеральную разность между новым сортом и всем стандартным сортом? Будет ли эта генеральная разность  тоже положительной? Этот вопрос можно решить путем оценки генерального значения средней разности на основе полученных сводных выборочных показателей.
тоже положительной? Этот вопрос можно решить путем оценки генерального значения средней разности на основе полученных сводных выборочных показателей.
Генеральный параметр изучаемой разности был оценен в форме доверительных границ с надежностью β 2 = 0,99 (исследование имело большое экономическое значение) следующим образом.
Проверка гипотез о различиях между долями респондентов. Часто исследователю приходится решать следующую проблему. Предположим, все опрошенные подразделяются на две подгруппы. (Это могут быть представители двух независимо построенных выборок, например выборка из жителей Москвы и выборка из жителей Санкт-Петербурга, а могут - лица, различия между которыми выявились в ходе анкетирования представителей одной и той же выборки респондентов, например те, у кого есть, и те, у кого нет высшего образования.) Исследователь должен выяснить, одинаково или по-разному распределились ответы представителей этих двух подгрупп на какой-либо определенный вопрос анкеты.
Пример 12.6
Исследование предпочтений в одежде (данные условны)
Пусть, например, нас интересует, различаются ли доли тех, кто носит джинсы, в Москве и Санкт-Петербурге. Пусть в каждом из этих городов были построены репрезентативные выборки и проведены опросы. Предположим, были получены следующие результаты (табл. 12.21).
Таблица 12.21. Респонденты, которые носят и не носят джинсы, по данным опросов лиц в возрасте до 35 лет в Москве и Санкт-Петербурге, человек
Мы видим, что в Москве носят джинсы 80% опрошенных, а в Санкт-Петербурге - лишь 60%. Но достаточно ли разницы в 20%, чтобы утверждать, что это не случайность, что вообще москвичи чаще склонны носить джинсы, чем петербуржцы?
Для ответа на этот вопрос воспользуемся знакомой нам статистикой z, имеющей стандартизованное нормальное распределение, которая помогла нам установить, что определенная в ходе другого опроса доля респондентов, осведомленных о новом продукте, значимо отличается от намеченного исследователем фиксированного значения.
Статистика для данного случая имеет следующий вид:
где p1 и р2 - доли носящих джинсы от числа опрошенных в Москве и Санкт-Петербурге (0,8 и 0,6 соответственно); - оценка стандартного отклонения разности долей р1 и р2.
Оценка стандартного отклонения разности долей рассчитывается по формуле
![]() (12.17)
(12.17)
где р - доля пользующихся джинсами среди всех опрошенных в двух выборках; n1 и n2 - число опрошенных в Москве и Санкт-Петербурге соответственно.
Величина р рассчитывается по формуле
В нашем примере имеем:

![]()
Поскольку нас интересует сам факт различия долей носящих джинсы в этих городах, а не превышения доли носящих джинсы в Москве по сравнению с такой долей в Санкт-Петербурге, нулевая и альтернативная гипотезы имеют вид:
Поэтому при прежней доверительной вероятности 0,95 пороговое значение на кривой нормального распределения равно 1,96.
А поскольку 4,36 > 1,96, нулевая гипотеза отвергается, т.е. данные опросов не противоречат утверждению, что доли носящих джинсы в Москве и Санкт-Петербурге различны.
Проверка гипотез о различиях между средними значениями. Часто требуется определить, являются ли случайными различия между средними значениями некоторой величины, рассчитанными по ответам представителей двух разных подвыборок респондентов. Например, исследователя может интересовать, действительно ли жители Москвы оценивают некоторый товар выше, чем жители Санкт-Петербурга, если средняя оценка этого товара по пятибалльной шкале респондентами-москвичами выше, чем респондентами-петербуржцами.
Для проверки такого рода гипотез используется статистика Стьюдента с числом степеней свободы (n1 + n0 - 1), где п1 и n2 - число объектов (в данном случае - респондентов) в каждой из двух выборок:
где и - средние значения оценок товара по данным опросов в Москве и в Санкт-Петербурге; - оценка стандартного отклонения разности интересующих нас средних значений между этими городами.
Последняя величина рассчитывается по формуле
где s - средневзвешенное среднеквадратическое отклонение оценок от соответствующих средних значений в каждой из выборок.
В свою очередь, величина s рассчитывается по формуле
 (12.21)
(12.21)
где x1,i и x2,j - оценки, полученные на i-м объекте из первой выборки и j-м объекте из второй выборки.
Такие проверки проводятся с помощью программного пакета SPSS (меню Analyze - Compare Means - Independent Samples T-test ).
Зависимые выборки
Обсуждавшаяся выше проблема касалась случая, когда сравниваются доли или средние значения определенным образом ответивших на интересующий нас вопрос в двух разных группах респондентов. Нередко, однако, нужно сравнить между собой не реакции разных респондентов (например, живущих в разных городах), а две реакции у одних и тех же респондентов. Так бывает, когда информация собирается дважды на одной и той же выборке из n объектов. Например, дважды опрашиваются одни и те же респонденты и нужно проверить гипотезу, что за время, прошедшее между опросами, их оценки изменились. Скажем, надо узнать, действительно ли повысилась после рекламной кампании доля участников панели, знающих о существовании некоторого товара. Или узнать, действительно ли о существовании товара А знают больше респондентов, чем о товаре В, или наблюдаемое по данным опроса различие - просто случайность.
В случае зависимых выборок для проверки гипотезы об отсутствии различий в средних значениях применяется следующая тестовая статистика с (n - 1) степенями свободы:
где и - средние значения оценок в первом и втором замерах соответственно;- стандартное отклонение определения различий в средних значениях оценок в двух замерах, рассчитываемое по формуле
Здесь - стандартное отклонение различий между оценками в двух замерах, которое, в свою очередь, рассчитывается по формуле
 (12.24)
(12.24)
где и - оценки на объектах в первом и втором замерах соответственно.
Отметим, что эти проверки можно провести с помощью программного пакета SPSS (меню Analyze - Compare Means - Pared Samples T-test ).
Обзор других задач анализа данных
Перед нами не было цели обсудить методы решения всего круга проблем, которые приходится время от времени решать при базовом анализе маркетинговых данных. Мы рассмотрели лишь те из них, которые используются чаще других.
В заключение раздела подчеркнем следующее. Как уже отмечалось, основной материал для отчета о маркетинговом исследовании дают таблицы частотных распределений и кросстабуляции. Структура этих таблиц может быть намечена заранее в той мере, в которой она связана с задачами исследования и выбранными подходами к их решению, т.е. исследователь сам назначает интересующие его группы респондентов и располагает их в столбцах таблиц сопряженности.
Однако нередко форма некоторых отчетных таблиц может быть окончательно установлена лишь на стадии углубленного анализа данных. Так, лишь на этой стадии можно провести сегментирование исследуемой совокупности и найти сегменты, наиболее резко отличающиеся друг от друга по реакции их представителей на маркетинговые действия фирмы. Построив затем соответствующие таблицы кросс-табуляции, можно детально изучить особенности каждого из сегментов, что позволит разработать набор эффективных маркетинговых комплексов.
Есть много методов углубленного анализа данных. Основное назначение большинства из них - подсказать исследователю, какой принцип сегментирования окажется наиболее удачным в том смысле, что построенные затем таблицы кросс-табуляции продемонстрируют наиболее яркие контрасты. Интересно, что многие исследователи, стремясь добиться краткости и ясности изложения материалов, а также не спеша раскрывать секреты своего мастерства, оставляют за рамками отчета примененный ими способ отыскания этой наиболее удачной формы таблиц. Мы рассмотрим два метода, дающих такие "подсказки", - методы кластерного и факторного анализов. Эти методы приспособлены для работы с часто встречающимися в маркетинговых исследованиях бинарными и метрическими шкалами.
Есть в арсенале исследователей и методы, позволяющие выяснить, как отнесутся потребители к тому или иному сочетанию свойств товара, насколько они ценят то или иное свойство товара. Это дает менеджерам рынка богатую пищу для размышлений при разработке маркетингового комплекса. Один из таких методов - совместный анализ (conjoint analysis ) - тоже будет рассмотрен нами в дальнейшем.
Пусть требуется оценить долю тех объектов заданной генеральной совокупности, которые удовлетворяют некоторому условию – генеральную долю . Для этого из генеральной совокупности выделяют выборку, и по результатам её обследования находят долю тех объектов, которые удовлетворяют условию – выборочную долю . Очевидно, что , где – объем выборки, – число тех её объектов, которые удовлетворяют условию . Выборочная доля в данном случае является той величиной, с помощью которой мы получим информацию о неизвестном значении генеральной доли.
Таким образом, выборочная доля является оценкой генеральной доли .
Пример. – доля бракованных деталей генеральной совокупности, – доля бракованных деталей в выборке. Условие (событие) – деталь, взятая наудачу из генеральной совокупности – бракована.
Простейший способ оценивания – точечное оценивание – подразумевает использование приближенного равенства .
Как и всякая оценка, выборочная доля является случайной величиной. Действительно, выборка из генеральной совокупности выделяется случайным образом. Соответственно то значение, которое примет выборочная доля, будет случайным.
Следующие теоремы характеризуют выборочную долю как случайную величину.
Теорема 1. Математическое ожидание выборочной доли равно генеральной доле:
Среднее квадратическое отклонение () выборочной доли вычисляется по формулам
![]()
– в случае повторной выборки и

– в случае бесповторной выборки, где – объем генеральной совокупности.
Напомним, что по определению среднего квадратического отклонения в случае повторной выборки имеем (аналогично в случае бесповторной выборки).
Замечание. При применении формул Теоремы 1 полагают
Теорема 2. Закон распределения выборочной доли неограниченно приближается к нормальному закону при неограниченном увеличении объема выборки.
Подобно тому, как мы это сделали в предыдущем параграфе, как следствие Теоремы 2, получаем формулу доверительной вероятности :

– в случае повторной выборки. Заменяя в последнем равенстве на , получаем формулу доверительной вероятности в случае бесповторной выборки.
По определению, величина , фигурирующая в формуле доверительной вероятности, называется предельной ошибкой выборки . Интервал называется доверительным интервалом.
Выше было указано, в чем состоит точечная оценка генеральной доли. Интервальное оценивание сводится, например, к вычислению значения доверительной вероятности при заданной предельной ошибке выборки.
Теорема 3. В случае повторной выборки выборочная доля является несмещенной и состоятельной оценкой генеральной доли.
Пример. Выборочные данные о надое молока для 100 коров из 1000 представлены таблицей:
1. Найти вероятность того, что доля всех коров с надоем молока более 40 ц отличается от такой доли в выборке не более чем на 0,05 (по абсолютной величине), для случая повторной и бесповторной выборок.
2. Найти границы, в которых с вероятностью 0,9596 заключена доля всех коров с надоем более 40 ц.
3. Сколько коров надо обследовать, чтобы с вероятностью 0,9786 для генеральной доли коров с надоем более 40 ц можно было гарантировать те же границы что и в п.2.
Решение.
Число коров с надоем более 40 ц равно 34 (, см. заданный вариационный ряд). Тогда ![]() .
.
Для нахождения доверительной вероятности п. 1 задания воспользуемся одноименной формулой при .
Пусть рассматриваемая выборка – повторная. Тогда по формуле Теоремы 1, учитывая Замечание, получаем
![]() .
.
Следовательно
Аналогично, в случае бесповторной выборки:
Доверительным в данном случае является интервал . Таким образом, неизвестное значение доли всех коров с надоем более 40 ц (0,29;0,39) с вероятностью 0,7109 в случае повторной выборки и с вероятностью 0,733
В п. 2 задания при заданном значении доверительной вероятности искомым является доверительный интервал. Поскольку значение выборочной доли известно, остается найти предельную ошибку выборки .
Пусть выборка – повторная. По условию, принимая во внимание формулу доверительной вероятности, имеем
 .
.
По таблице значений функции Лапласа найдем такое , что : . Тогда и, используя найденное выше значение , получаем
Соответственно, доверительным будет интервал:
Пусть выборка – бесповторная. Аналогично предыдущему, получаем предельную ошибку выборки
и доверительный интервал:
Таким образом, доля всех коров с надоем молока более 40 ц с вероятностью 0,9596 накрывается доверительным интервалом (0,243; 0,437) в случае повторной выборки и интервалом (0,248; 0,432) в случае бесповторной выборки.
В п. 3 по заданным значениям доверительной вероятности и предельной ошибки выборки найдем необходимый объем выборки. Из начла решения заимствуем значение выборочной доли , найденное по исходному вариационному ряду.
Оценка статистической значимости результатов исследования
Под статистической значимостью данных понимают степень их соответствия отображаемой действительности, т.е. статистически значимыми данными считаются те, которые не искажают и правильно отражают объективную реальность.
Оценить статистическую значимость результатов исследования – означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность. Оценка статистической значимости необходима для понимания того, насколько по части явления можно судить о явлении в целом и его закономерностях.
Оценка статистической значимости результатов исследования складывается из:
1. ошибок репрезентативности (ошибок средних и относительных величин) - m ;
2. доверительных границ средних или относительных величин;
3. достоверности разности средних или относительных величин по критерию t .
Стандартная ошибка средней арифметической или ошибка репрезентативности характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин. Стандартная ошибка среднего вычисляется по формуле:
В современной научной литературе средняя арифметическая записывается вместе с ошибкой репрезентативности:
или вместе со среднеквадратическим отклонением:
В качестве примера рассмотрим данные по 1500 городских поликлиник страны (генеральная совокупность). Среднее число пациентов, обслуживающихся в поликлинике равно 18150 человек. Случайный отбор 10 % объектов (150 поликлиник) дает среднее число пациентов, равное 20051 человек. Ошибка выборки, очевидно связанная с тем, что не все 1500 поликлиник попали в выборку, равна разности между этими средними – генеральным средним (M ген) и выборочным средним (М выб). Если сформировать другую выборку того же объема из нашей генеральной совокупности, она даст другую величину ошибки. Все эти выборочные средние при достаточно больших выборках распределены нормально вокруг генеральной средней при достаточно большом числе повторений выборки одного и того же числа объектов из генеральной совокупности. Стандартная ошибка среднего m - это неизбежный разброс выборочных средних вокруг генеральной средней.
В случае, когда результаты исследования представлены относительными величинами (например, процентными долями) – рассчитывается стандартная ошибка доли:

где P – показатель в %, n – количество наблюдений.
Результат отображается в виде (P ± m)%. Например, процент выздоровления среди больных составил (95,2±2,5)%.
В том случае, если число элементов совокупности , то при расчете стандартных ошибок среднего и доли в знаменателе дроби вместо необходимо ставить .
Для нормального распределения (распределение выборочных средних является нормальным) известно, какая часть совокупности попадает в любой интервал вокруг среднего значения. В частности:
· 68,3% всех выборочных средних попадают в интервал
· 95,5% - в интервал
· 99,7% - в интервал
На практике проблема заключается в том, что характеристики генеральной совокупности нам неизвестны, а выборка делается именно с целью их оценки. Это означает, что если мы будем делать выборки одного и того же объема n из генеральной совокупности, то в 68,3% случаев на интервале будет находиться значение M (оно же в 95,5% случаев будет находиться на интервале и в 99,7% случаев – на интервале).
Поскольку реально делается только одна выборка, то формулируется это утверждение в терминах вероятности: с вероятностью 68,3% среднее значение признака в генеральной совокупности заключено в интервале, с вероятностью 95,5%- в интервале и т.д.
На практике вокруг выборочного значения строится такой интервал, который бы с заданной (достаточно высокой) вероятностью – доверительной вероятностью – «накрывал» бы истинное значение этого параметра в генеральной совокупности. Этот интервал называется доверительным интервалом .
Доверительная вероятность P – это степень уверенности в том, что доверительный интервал действительно будет содержать истинное (неизвестное) значение параметра в генеральной совокупности.
Например, если доверительная вероятность Р равна 90%, то это означает, что 90 выборок из 100 дадут правильную оценку параметра в генеральной совокупности. Соответственно, вероятность ошибки, т.е. неверной оценки генерального среднего по выборке, равна в процентах: . Для данного примера это значит, что 10 выборок из 100 дадут неверную оценку.
Очевидно, что степень уверенности (доверительная вероятность) зависит от величины интервала: чем шире интервал, тем выше уверенность, что в него попадет неизвестное значение для генеральной совокупности . На практике для построения доверительного интервала берется, как минимум, удвоенная ошибка выборки, чтобы обеспечить уверенность не менее 95,5%.
Определение доверительных границ средних и относительных величин позволяет найти два их крайних значения – минимально возможное и максимально возможное, в пределах которых изучаемый показатель может встречаться во всей генеральной совокупности. Исходя из этого, доверительные границы (или доверительный интервал) - это границы средних или относительных величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность.
Доверительный интервал может быть переписан в виде: , где t – доверительный критерий.
Доверительные границы средней арифметической величины в генеральной совокупности определяют по формуле:
М ген = М выб + t m M
для относительной величины:
Р ген = Р выб + t m Р
где М ген и Р ген - значения средней и относительной величины для генеральной совокупности; М выб и Р выб - значения средней и относительной величины, полученные на выборочной совокупности; m M и m P - ошибки средней и относительной величин; t - доверительный критерий (критерий точности, который устанавливается при планировании исследования и может быть равен 2 или 3); t m - это доверительный интервал или Δ – предельная ошибка показателя, полученного при выборочном исследовании.
Следует отметить, что величина критерия t в определенной мере связана с вероятностью безошибочного прогноза (р), выраженной в %. Ее избирает сам исследователь, руководствуясь необходимостью получить результат с нужной степенью точности. Так, для вероятности безошибочного прогноза 95,5% величина критерия t составляет 2, для 99,7% - 3.
Приведенные оценки доверительного интервала приемлемы лишь для статистических совокупностей с количеством наблюдений более 30. При меньшем объеме совокупности (малых выборках) для определения критерия t пользуются специальными таблицами. В данных таблицах искомое значение находится на пересечении строки, соответствующей численности совокупности (n-1) , и столбца, соответствующего уровню вероятности безошибочного прогноза (95,5%; 99,7%), выбранному исследователем. В медицинских исследованиях при установлении доверительных границ любого показателя принята вероятность безошибочного прогноза 95,5% и более. Это означает, что величина показателя, полученная на выборочной совокупности должна встречаться в генеральной совокупности как минимум в 95,5% случаев.
1. Вопросы по теме занятия:
1. Актуальность показателей разнообразия признака в статистической совокупности.
2. Общая характеристика абсолютных показателей вариации.
3. Среднее квадратическое отклонение, расчет, применение.
4. Относительные показатели вариации.
5. Медиана, квартильная оценка.
6. Оценка статистической значимости результатов исследования.
7. Стандартная ошибка средней арифметической, формула расчета, пример использования.
8. Расчет доли и ее стандартной ошибки.
9. Понятие доверительной вероятности, пример использования.
10. Понятие доверительного интервала, его применение.
2. Тестовые задания по теме с эталонами ответов:
1. К АБСОЛЮТНЫМ ПОКАЗАТЕЛЯМ ВАРИАЦИИ ОТНОСИТСЯ
1) коэффициент вариации
2) коэффициент осцилляции
4) медиана
2. К ОТНОСИТЕЛЬНЫМ ПОКАЗАТЕЛЯМ ВАРИАЦИИ ОТНОСИТСЯ
1) дисперсия
4) коэффициент вариации
3. КРИТЕРИЙ, КОТОРЫЙ ОПРЕДЕЛЯЕТСЯ КРАЙНИМИ ЗНАЧЕНИЯМИ ВАРИАНТ В ВАРИАЦИОННОМ РЯДУ
2) амплитуда
3) дисперсия
4) коэффициент вариации
4. РАЗНОСТЬ КРАЙНИХ ВАРИАНТ – ЭТО
2) амплитуда
3) среднее квадратичное отклонение
4) коэффициент вариации
5. СРЕДНИЙ КВАДРАТ ОТКЛОНЕНИЙ ИНДИВИДУАЛЬНЫХ ЗНАЧЕНИЙ ПРИЗНАКА ОТ ЕГО СРЕДНЕЙ ВЕЛИЧИНЫ – ЭТО
1) коэффициент осцилляции
2) медиана
3) дисперсия
6. ОТНОШЕНИЕ РАЗМАХА ВАРИАЦИИ К СРЕДНЕЙ ВЕЛИЧИНЕ ПРИЗНАКА – ЭТО
1) коэффициент вариации
2) среднее квадратичное отклонение
4) коэффициент осцилляции
7. ОТНОШЕНИЕ СРЕДНЕГО КВАДРАТИЧНОГО ОТКЛОНЕНИЯ К СРЕДНЕЙ ВЕЛИЧИНЕ ПРИЗНАКА – ЭТО
1) дисперсия
2) коэффициент вариации
3) коэффициент осцилляции
4) амплитуда
8. ВАРИАНТА, КОТОРАЯ НАХОДИТСЯ В СЕРЕДИНЕ ВАРИАЦИОННОГО РЯДА И ДЕЛИТ ЕГО НА ДВЕ РАВНЫЕ ЧАСТИ – ЭТО
1) медиана
3) амплитуда
9. В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ ПРИ УСТАНОВЛЕНИИ ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ЛЮБОГО ПОКАЗАТЕЛЯ ПРИНЯТА ВЕРОЯТНОСТЬ БЕЗОШИБОЧНОГО ПРОГНОЗА
10. ЕСЛИ 90 ВЫБОРОК ИЗ 100 ДАЮТ ПРАВИЛЬНУЮ ОЦЕНКУ ПАРАМЕТРА В ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ, ТО ЭТО ОЗНАЧАЕТ, ЧТО ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ P РАВНА
11. В СЛУЧАЕ, ЕСЛИ 10 ВЫБОРОК ИЗ 100 ДАЮТ НЕВЕРНУЮ ОЦЕНКУ, ВЕРОЯТНОСТЬ ОШИБКИ РАВНА
12. ГРАНИЦЫ СРЕДНИХ ИЛИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН, ВЫХОД ЗА ПРЕДЕЛЫ КОТОРЫХ ВСЛЕДСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ ИМЕЕТ НЕЗНАЧИТЕЛЬНУЮ ВЕРОЯТНОСТЬ – ЭТО
1) доверительный интервал
2) амплитуда
4) коэффициент вариации
13. МАЛОЙ ВЫБОРКОЙ СЧИТАЕТСЯ ТА СОВОКУПНОСТЬ, В КОТОРОЙ
1) n меньше или равно 100
2) n меньше или равно 30
3) n меньше или равно 40
4) n близко к 0
14. ДЛЯ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО ПРОГНОЗА 95% ВЕЛИЧИНА КРИТЕРИЯ t СОСТАВЛЯЕТ
15. ДЛЯ ВЕРОЯТНОСТИ БЕЗОШИБОЧНОГО ПРОГНОЗА 99% ВЕЛИЧИНА КРИТЕРИЯ t СОСТАВЛЯЕТ
16. ДЛЯ РАСПРЕДЕЛЕНИЙ, БЛИЗКИХ К НОРМАЛЬНОМУ, СОВОКУПНОСТЬ СЧИТАЕТСЯ ОДНОРОДНОЙ, ЕСЛИ КОЭФФИЦИЕНТ ВАРИАЦИИ НЕ ПРЕВЫШАЕТ
17. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ, ЧИСЛОВЫЕ ЗНАЧЕНИЯ КОТОРЫХ НЕ ПРЕВЫШАЮТ 25% МАКСИМАЛЬНО ВОЗМОЖНОГО В ДАННОМ РЯДУ – ЭТО
2) нижний квартиль
3) верхний квартиль
4) квартиль
18. ДАННЫЕ, КОТОРЫЕ НЕ ИСКАЖАЮТ И ПРАВИЛЬНО ОТРАЖАЮТ ОБЪЕКТИВНУЮ РЕАЛЬНОСТЬ, НАЗЫВАЮТСЯ
1) невозможные
2) равновозможные
3) достоверные
4) случайные
19. СОГЛАСНО ПРАВИЛУ "ТРЕХ СИГМ", ПРИ НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ ПРИЗНАКА В ПРЕДЕЛАХ ![]() БУДЕТ НАХОДИТЬСЯ
БУДЕТ НАХОДИТЬСЯ
1) 68,3% вариант
2) 95,5% вариант
3) 99,7% вариант
4) 50,0% вариант
20. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ, СООТВЕТСТВУЮЩИЙ СТЕПЕНИ ВЕРОЯТНОСТИ ![]() (n>30), СОСТАВЛЯЕТ
(n>30), СОСТАВЛЯЕТ
21. КОЭФФИЦИЕНТ ВАРИАЦИИ ПРИМЕНЯЕТСЯ
1) для характеристики нормальности распределения
2) для характеристики однородности совокупности
3) для определения среднеквадратического отклонения
4) для определения необходимого объема выборки
22. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ ВЕЛИЧИНОЙ ДО 75% ОТ МАКСИМАЛЬНО ВОЗМОЖНЫХ ЗНАЧЕНИЙ – ЭТО
1) нижний квартиль
3) верхний квартиль
4) квартиль
23. ВАРИАНТА, ОТДЕЛЯЮЩАЯ ВАРИАНТЫ С ЧИСЛОВЫМ ЗНАЧЕНИЕМ ДО 50% ОТ МАКСИМАЛЬНО ВОЗМОЖНОГО – ЭТО
1) квартиль
2) нижний квартиль
4) верхний квартиль
24 КОЭФФИЦИЕНТ ВАРИАЦИИ ВЫРАЖАЕТСЯ
1) в сантиметрах
2) в числе пациентов
3) в числе вариаций
4) в процентах
25. В СЛУЧАЕ СИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНО СРЕДНЕГО АРИФМЕТИЧЕСКОГО ДЛЯ ЕГО ХАРАКТЕРИСТИКИ ИСПОЛЬЗУЮТСЯ
1) медиана и процентили
2) лимит и среднеквадратичное отклонение
26. В СЛУЧАЕ АСИММЕТРИЧНОСТИ РАСПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНО СРЕДНЕГО АРИФМЕТИЧЕСКОГО ДЛЯ ЕГО ХАРАКТЕРИСТИКИ ИСПОЛЬЗУЮТСЯ
1) медиана и процентили
2) медиана и среднеквадратичное отклонение
3) среднее арифметическое и среднеквадратичное отклонение
4) среднее арифметическое и процентили
27. ПРИ ЗНАЧЕНИИ КОЭФФИЦИЕНТА ВАРИАЦИИ 15% СТЕПЕНЬ РАЗНООБРАЗИЯ ПРИЗНАКА ОЦЕНИВАЕТСЯ КАК
2) средняя
3) сильная
4) равномерная
28. ГРАНИЦЫ СРЕДНИХ ИЛИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН, ВЫХОД ЗА ПРЕДЕЛЫ КОТОРЫХ ВСЛЕДСТВИЕ СЛУЧАЙНЫХ КОЛЕБАНИЙ ИМЕЕТ НЕЗНАЧИТЕЛЬНУЮ ВЕРОЯТНОСТЬ – ЭТО
1) доверительный интервал
2) доверительный критерий
3) стандартная ошибка
4) среднее квадратическое отклонение
29. ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТА ВАРИАЦИИ НЕОБХОДИМА СЛЕДУЮЩАЯ ВЕЛИЧИНА
1) стандартная ошибка
2) медиана
3) среднее квадратическое отклонение
4) доверительный интервал
30. НЕДОСТАТКОМ ЛИМИТА И АМПЛИТУДЫ КАК КРИТЕРИЕВ ВАРИАБЕЛЬНОСТИ ЯВЛЯЕТСЯ
1) необходимость нормального распределения для их расчета
2) зависимость от крайних значений переменных
3) зависимость от числа наблюдений
4) зависимость от средних значений переменных
Эталоны ответов на тестовые задания:
| вопрос | ||||||||||
| ответ | ||||||||||
| вопрос | ||||||||||
| ответ | ||||||||||
| вопрос | ||||||||||
| ответ |