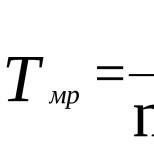Абсолютные и относительные величины. Детерминированное факторное исследование. Статистические показатели, их виды

В этой статье мы детально разберем модуль числа . Мы дадим различные определения модуля числа, введем обозначения и приведем графические иллюстрации. При этом рассмотрим различные примеры нахождения модуля числа по определению. После этого мы перечислим и обоснуем основные свойства модуля. В конце статьи поговорим о том, как определяется и находится модуль комплексного числа.

Навигация по странице.

Модуль числа – определение, обозначение и примеры

Сначала введем обозначение модуля числа . Модуль числа a будем записывать как , то есть, слева и справа от числа будем ставить вертикальные черточки, образующие знак модуля. Приведем пару примеров. Например, модуль −7 можно записать как ; модуль 4,125 записывается как , а модуль имеет запись вида .

Следующее определение модуля относится к , а следовательно, и к , и к целым, и к рациональным, и к иррациональным числам, как к составляющим частям множества действительных чисел. О модуле комплексного числа мы поговорим в .

Определение.

Модуль числа a – это либо само число a , если a – положительное число, либо число −a , противоположное числу a , если a – отрицательное число, либо 0 , если a=0 .

Озвученное определение модуля числа часто записывают в следующем виде , эта запись означает, что , если a>0 , , если a=0 , и , если a<0 .

Запись можно представить в более компактной форме . Эта запись означает, что , если (a больше или равно 0 ), и , если a<0 .

Также имеет место и запись . Здесь отдельно следует пояснить случай, когда a=0 . В этом случае имеем , но −0=0 , так как нуль считают числом, которое противоположно самому себе.

Приведем примеры нахождения модуля числа с помощью озвученного определения. Для примера найдем модули чисел 15 и . Начнем с нахождения . Так как число 15 – положительное, то его модуль по определению равен самому этому числу, то есть, . А чему равен модуль числа ? Так как - отрицательное число, то его модуль равен числу, противоположному числу , то есть, числу . Таким образом, .

В заключение этого пункта приведем один вывод, который очень удобно применять на практике при нахождении модуля числа. Из определения модуля числа следует, что модуль числа равен числу под знаком модуля без учета его знака , а из рассмотренных выше примеров это очень отчетливо видно. Озвученное утверждение объясняет, почему модуль числа называют еще абсолютной величиной числа . Так модуль числа и абсолютная величина числа – это одно и то же.

Модуль числа как расстояние

Геометрически модуль числа можно интерпретировать как расстояние . Приведем определение модуля числа через расстояние .

Определение.

Модуль числа a – это расстояние от начала отсчета на координатной прямой до точки, соответствующей числу a.

Данное определение согласуется с определением модуля числа, данного в первом пункте. Поясним этот момент. Расстояние от начала отсчета до точки, которой соответствует положительное число, равно этому числу. Нулю соответствует начало отсчета, поэтому расстояние от начала отсчета до точки с координатой 0 равно нулю (не нужно откладывать ни одного единичного отрезка и ни одного отрезка, составляющего какую-нибудь долю единичного отрезка, чтобы от точки O попасть в точку с координатой 0 ). Расстояние от начала отсчета до точки с отрицательной координатой равно числу, противоположному координате данной точки, так как равно расстоянию от начала координат до точки, координатой которой является противоположное число.

Например, модуль числа 9 равен 9 , так как расстояние от начала отсчета до точки с координатой 9 равно девяти. Приведем еще пример. Точка с координатой −3,25 находится от точки O на расстоянии 3,25 , поэтому .

Озвученное определение модуля числа является частным случаем определения модуля разности двух чисел.

Определение.

Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b .

То есть, если даны точки на координатной прямой A(a) и B(b) , то расстояние от точки A до точки B равно модулю разности чисел a и b . Если в качестве точки В взять точку O (начало отсчета), то мы получим определение модуля числа, приведенное в начале этого пункта.

Определение модуля числа через арифметический квадратный корень

Иногда встречается определение модуля через арифметический квадратный корень .

Для примера вычислим модули чисел −30 и на основании данного определения. Имеем . Аналогично вычисляем модуль двух третьих: .

Определение модуля числа через арифметический квадратный корень также согласуется с определением, данным в первом пункте этой статьи. Покажем это. Пусть a – положительное число, при этом число −a – отрицательное. Тогда и , если же a=0 , то .

Свойства модуля

Модулю присущ ряд характерных результатов - свойства модуля . Сейчас мы приведем основные и наиболее часто используемые из них. При обосновании этих свойств мы будем опираться на определение модуля числа через расстояние.

Начнем с самого очевидного свойства модуля – модуль числа не может быть отрицательным числом . В буквенном виде это свойство имеет запись вида для любого числа a . Это свойство очень легко обосновать: модуль числа есть расстояние, а расстояние не может выражаться отрицательным числом.

Переходим к следующему свойству модуля. Модуль числа равен нулю тогда и только тогда, когда это число есть нуль . Модуль нуля есть нуль по определению. Нулю соответствует начало отсчета, никакая другая точка на координатной прямой нулю не соответствует, так как каждому действительному числу поставлена в соответствие единственная точка на координатной прямой. По этой же причине любому числу, отличному от нуля, соответствует точка, отличная от начала отсчета. А расстояние от начала отсчета до любой точки, отличной от точки O , не равно нулю, так как расстояние между двумя точками равно нулю тогда и только тогда, когда эти точки совпадают. Приведенные рассуждения доказывают, что нулю равен лишь модуль нуля.

Идем дальше. Противоположные числа имеют равные модули, то есть, для любого числа a . Действительно, две точки на координатной прямой, координатами которых являются противоположные числа, находятся на одинаковом расстоянии от начала отсчета, значит модули противоположных чисел равны.

Следующее свойство модуля таково: модуль произведения двух чисел равен произведению модулей этих чисел , то есть, . По определению модуль произведения чисел a и b равен либо a·b , если , либо −(a·b) , если . Из правил умножения действительных чисел следует, что произведение модулей чисел a и b равно либо a·b , , либо −(a·b) , если , что доказывает рассматриваемое свойство.

Модуль частного от деления a на b равен частному от деления модуля числа a на модуль числа b , то есть, . Обоснуем это свойство модуля. Так как частное равно произведению , то . В силу предыдущего свойства имеем . Осталось лишь воспользоваться равенством , которое справедливо в силу определения модуля числа.

Следующее свойство модуля записывается в виде неравенства: , a , b и c – произвольные действительные числа. Записанное неравенство представляет собой ни что иное как неравенство треугольника . Чтобы это стало понятно, возьмем точки A(a) , B(b) , C(c) на координатной прямой, и рассмотрим вырожденный треугольник АВС , у которого вершины лежат на одной прямой. По определению модуля разности равен длине отрезка АВ , - длине отрезка АС , а - длине отрезка СВ . Так как длина любой стороны треугольника не превосходит сумму длин двух других сторон, то справедливо неравенство , следовательно, справедливо и неравенство .

Только что доказанное неравенство намного чаще встречается в виде . Записанное неравенство обычно рассматривают как отдельное свойство модуля с формулировкой: «Модуль суммы двух чисел не превосходит сумму модулей этих чисел ». Но неравенство напрямую следует из неравенства , если в нем вместо b положить −b , и принять c=0 .

Модуль комплексного числа

Дадим определение модуля комплексного числа . Пусть нам дано комплексное число , записанное в алгебраической форме , где x и y – некоторые действительные числа, представляющие собой соответственно действительную и мнимую части данного комплексного числа z , а – мнимая единица.

Определение .Абсолютной величиной (илимодулем ) действительного числа(обозначается) называется неотрицательное число, удовлетворяющее условиям:

Ясно, что всегда

. (3.1)

Свойства абсолютных величин:

1)
; 2)
; 3)
; 4)
.

Доказательство. 1) Если
, тов силу (3.1). Если
, то. Первое свойство доказано.

2) Имеем , отсюда
. Второе свойство доказано.

3) , третье свойство доказано.

Четвертое свойство доказывается так же, как свойство 3).

Замечание . Свойство 1) распространяется на любое число слагаемых, свойство 3) – на любое число сомножителей.

Отметим также, что , т.е.х удовлетворяет неравенству
тогда и только тогда, когда принадлежит интервалу
.

Геометрический смысл модуля действительного числа состоит в том, что равен расстоянию от точких на числовой прямой до нуля.

§ 4. Понятие числовой последовательности. Бесконечно большая и бесконечно малая последовательности, их свойства

Определение 1. Если каждому значениюn из множества натуральных чисел
ставится в соответствие по определенному закону некоторое действительное число, то множество занумерованных действительных чисел называетсячисловой последовательностью
.

– члены последовательности,
– сокращенная запись последовательности. Например,
.

Определение 2. Пусть даны две последовательности
и
. Последовательностиназываются соответственно суммой, разностью, произведением и частным последовательностей
и
.

Определение 3. Последовательность
называетсяограниченной , если множество ее членов ограничено, т.е. существует число
, такое, что
. Последовательность
называетсяограниченной сверху (снизу ) , если существует числоМ , такое, что.

Если последовательность
неограниченна, то для любого числа
найдется номерn такой, что
. Ясно, что если последовательность ограничена только снизу или только сверху, то она неограниченна. Среди неограниченных последовательностей выберем бесконечно большие последовательности.

Определение 4. Последовательность
называетсябесконечно большой , если для любого
найдется номерN , такой, что
для всех
.

Всякая бесконечно большая последовательность неограниченна, но не всякая неограниченная последовательность бесконечно большая. Примером этого может служить последовательность .

Определение 5. Последовательность
называетсябесконечно малой , если для любого
найдется номерN , такой, что
для всех
.

Установим основные свойства бесконечно малых последовательностей.

Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство . Пусть
и
– бесконечно малые последовательности. Возьмем
произвольно и положим
. По определению 5 длянайдутся номераи
, такие, что
для всех
и
для всех
. Положим
. Тогда для всех
и по определению 5 последовательность
бесконечно малая. Теорема доказана.

Аналогично доказываются

Теорема 2. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Следствие . Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 3. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

(Можно поручить студентам доказать теоремы 2, 3 и следствие самостоятельно ).

Теорема 4. Всякая бесконечно малая последовательность ограничена.

Доказательство . Пусть
– бесконечно малая последовательность. Положим
N , такой, что
для всех
. Обозначим. Тогда
для всехn . Теорема доказана.

Следствие теорем 3и 4. Произведение двух (любого конечного числа) бесконечно малых последовательностей есть бесконечно малая последовательность.

Теорема 5. Если все члены бесконечно малой последовательности равны одному и тому же числус , то
.

Доказательство . Предположим противное, т.е. что
. Возьмем
. По определению 5 найдется номерN , такой, что
для всех
, т.е.
для всех
, а этого не может быть, так как
для всехn . Противоречие доказывает утверждение теоремы.

Теорема 6. Если
– бесконечно большая последовательность, то– бесконечно малая последовательность.

Доказательство . Возьмем
произвольно и положим
. Тогда по определению 4 найдется номерN , такой, что
для всех значений
. Отсюда
для всех
, т.е.– бесконечно малая последовательность по определению 5. Теорема доказана.

Теорема 7. Если
– бесконечно малая последовательность и все члены этой последовательности отличны от нуля, то последовательность– бесконечно большая (доказать самостоятельно ).

Абсолютные цифры - «ясный» способ показать, сколько и чего у нас есть. Сколько у меня яблок? Четыре. Здесь все понятно, и никакая визуализация не нужна. Нам нравится знать точное количество, поскольку это дает нам ощущение определенности и способность быть точными.

Оба эти фактора в совокупности чрезвычайно важны для того, чтобы мы могли с уверенно­стью принимать важные решения (к примеру, о том, сколько яблок отда­вать Тому).

Абсолютное количество придает больше уверенности в цифрах

Однако у них есть и свои проблемы. Прежде всего, мы как люди доволь­но плохо усваиваем «большие» цифры. Самое значительное количество, которое можно представить себе без сознательного усилия, равно пяти (подумайте об этом в следующий раз, когда кто-то начнет разбрасывать­ся «миллиардами»). Это не значит, что мы не можем представить себе огромные числа; разумеется, можем, но вряд ли сумеем изобразить в виде картинки. Поскольку большинство людей на самом деле не способны представить себе большие числа, визуальное сравнение одного числа или количества с другим помогает нам понять, о чем речь.

К примеру, в случае четверых людей (Тома, Дика, Гарри и меня самого) и четырех яблок довольно просто понять, по каким признакам они сравни­ваются. Однако, что если бы у меня было 39 яблок или, скажем, 72 тысячи? Понятно, что получить правильный ответ можно простым делением в стол­бик, однако (и особенно в случаях, когда мы заинтересованы в быстрой оценке) нам поможет и картинка со сравнительными показателями.

Нам не нужно пересчитывать ко­личество яблок, чтобы их поделить. Достаточно визуального сравне­ния обоих чисел

Самое простое, очевидное и часто используемое для сравнения чис­ло - сотня. С ее помощью мы можем получить процентный показатель. А как мы знаем, это отличный способ дать количественную оценку, срав­нив части с целым или одно число с другим.

Использование стандарта для сравнения типа процентов часто упрощает задачу понять, что озна­чают большие числа

Использование стандарта для сравнения помогает также смягчить вторую проблему с абсолютными количествами: когда абсолютные коли­чества становятся слишком большими (или слишком малыми), их сложно показывать на графике любого вида. Особенно, если мы пытаемся изобра­зить большое количество рядом с небольшим*. Переключиться на срав­нительные значения зачастую означает позволить себе больше гибкости, сделать цифры более заметными.

*Математики знают, насколько сложно бывает управлять (или хотя бы фиксировать на бумаге) крайне большими или крайне ма­лыми числа, поэтому они изобре­ли для решения этой проблемы способ экспоненциальной записи. Не хочу с ними спорить, однако скажу, что простые картинки по­могают быстрее понять, что озна­чают большие числа. Изучив их, мы можем принять решение, нуж­ны ли нам более детальные мате­матические расчеты.

График, показывающий сравнительные величины, обеспечивает нас большей степенью визуаль­ной гибкости, чем график, пока­зывающий абсолютные значения

Рассмотрим несколько примеров.

По яблоку в день

Когда кто-нибудь говорит слово «яблоко», большинству из нас на ум при­ходит она из двух картинок - фрукт или компьютер. Как мы знаем из пре­дыдущего разговора о модели 6 х 6, в нашем распоряжении есть крайне простой и эффективный способ изобразить различия между ними - про­стой портрет.

О каких яблоках идет речь? Порт­рет помогает увидеть разницу

Но что делать, если собеседник говорит: «Я имею в виду фрукт. Что значит фраза ”an apple a day keeps doctor away*”?» Здесь необходим со­вершенно иной образ. Почему не придется посещать докторов? Связано ли это с тем, что яблоко красного цвета? Вряд ли. Связано ли это с тем, что обычно яблоко имеет форму шара? Нет. Может быть, дело в том, что яблоки приятно есть? Возможно, однако наш личный опыт показывает, насколько сильно доктора любят измерять здоровье - они меряют нашу температу­ру, изучают данные о кровяном давлении, взвешивают нас, подсчитывают показатели холестерина и т. д. Возможно, что в яблоках есть нечто изме­ряемое, и оно позволяет нам спокойно жить без медицинского персонала.

*Что можно перевести пример но так: «В день по яблоку съедаешь - докторов не посещаешь!

Каким образом мы можем измерить нечто, связанное с яблоками и по­могающее нам оставаться здоровыми?

График показывает, какие именно показатели позволяют яблокам становиться эффективными ре­пеллентами против врачей

Цена на бананы

Говоря о фруктах, давайте на минуту вернемся к нашему покупателю ба­нанов. Помните, в чем мы были заинтересованы? Мы хотели узнать, имеет ли финансовый смысл покупка бананов у поставщика, который продает их по более низкой цене, но при этом находится значительно дальше прежнего. Нас совершенно не интересуют никакие вопросы, связанные с бананами, кроме издержек. Чтобы их увидеть, нам понадобится график*.

Он отражает оптовые цены на бананы в нескольких вымышленных странах-производителях: Бурола, Хаулу, Вестанго и наш нынешний поставщик Киксос:

*Цифры и географические объекты в этом упражнении также полно­стью вымышлены. Пожалуйста, не принимайте никаких решений о покупке бананов, основываясь только на том, что видите в этой книге.

Мы видим, что бананы из Бурола значительно дешевле, чем бананы от нашего нынешнего поставщи­ка Киксос

Этот график показывает величины транспортных расходов по доставке из этих четырех стран:

Если ориентироваться исключительно на параметр «сколько» и со­вместить два простых графика, то ответ очевиден: мы должны перестать покупать бананы в стране Киксос и переключиться на Бурола:

Даже при увеличении затрат на транспортировку бананы Бурола обойдутся нам значительно дешевле

Разумеется, глядя лишь на картинки, иллюстрирующие параметр «сколько», мы упускаем кое-что из виду. Помните, мы были крупным покупателем бананов в Киксосе на протяжении ряда лет. Что произой­дет в этой стране, если мы перестанем покупать у нее бананы? Графики не могут дать нам ответа, однако способны показать, что любое снижение объема продажи бананов серьезно повредит экономике Киксоса:

Мы крупный покупатель бананов в Киксосе, а торговля ими состав­ляет почти две трети экономики этой страны. Что произойдет, если мы перестанем покупать там бананы?

Грубо говоря, это совершенно не интересует нас с точки зрения «сколько». Однако когда-нибудь это вполне может стать нашей проблемой. Может быть, стоит обсудить более низкую цену? Или просто расстаться с Киксосом, найти другого поставщика или другой способ заработать день­ги? Кто знает? Разумеется, графики не могут дать нам ответа. Главный урок здесь в другом: всегда необходимо помнить, что мы измеряем, а что нет. Ответ на вопрос «сколько» (первая картинка, на которую обраща­ет внимание бизнесмен) всегда упускает из вида важную информацию из других источников, то есть другие точки зрения на проблему.

ВАША ОЧЕРЕДЬ РИСОВАТЬ ГРАФИК

Изучите описанные ниже упражнения по созданию графиков и выберите для работы одно из них (если вам нравится отвечать на вопрос «сколько», не откажите себе в удовольствии и сделайте оба). Мое решение приведено в приложении на с. 370.

Вариант графика /: Кто как видит?

Вчера мы говорили о типах людей, решающих визуальные проблемы, и о том, что каждый из нас относится к одной из следующих категорий:

Черная Ручка;

Желтая Ручка;

Красная Ручка.

В ходе сотен встреч я просил участников поднимать руки в ответ на вопрос, какая из этих категорий лучше всего описывает каждого из них. В большинстве случаев руки поднимаются вверх в следующей последовательности: чуть больше четверти участников относит себя к первой категории, примерно половина-ко второй и чуть менее четверти - к третьей. Один или два человека вообще не поднимают руки. На что это похоже?

В ходе одного собрания, на котором присутствовали сотни людей из крупнейшего объединения преподавателей по всей стране, я задал тот же самый вопрос. Результат оказался совсем не таким, который я привык видеть в других группах: к первой категории себя отнесла лишь пара человек, ко второй - четверо, а к третьей-добрая сотня слушателей. На этот раз никто из участников не воздержался. На что это похоже, особенно если сравнить с частью 1?*

*Это подлинная история, которая оказалась для меня настоящим шоком. Самое огромное исключение из обще­го правила проявилось, когда я провел этот (не вполне научный) опрос среди доброй сотни представителей Национальной ассоциации образования - почти все они посчитали себя Красными Ручками! Здесь можно много сказать, насколько несовершенным для таких людей будет способ решения проблем с помощью кар­тинок, однако скорее всего мы предадимся домыслам. Для того чтобы понять, что означала такая ситуация на самом деле, необходим набор более валидных тестов (проведенный человеком, разбирающимся в стати­стике лучше, чем я). Нам предстоит узнать чуть больше о преподавателях, образовательной системе, пони­мании интеллекта или куче других вещей. Ау, аспиранты - вам не нужна тема для диссертации?

Вариант графика 2. У вас температура

В гл. I этой книги неравенство было определено, как мы помним, в терминах множества положительных чисел. Напомним также, что для справедливости отдельных результатов гл. II, например теоремы 5, касающейся умножения неравенств, было необходимо потребовать положительности некоторых чисел, фигурирующих в условиях теоремы. В теореме 7 той же главы появляются степени с дробными показателями, которые иногда могут не оказаться даже действительными числами, если не оговорить положительности числа, возводимого в дробную степень; чтобы убедиться в этом, достаточно рассмотреть, например, для Многие из основных неравенств, которые выводятся в гл. IV, содержат такие степени с дробными показателями. Естественно, что и далее мы часто будем ограничиваться рассмотрением положительных чисел или неотрицательных чисел (т. е. положительных чисел и числа нуль).

В прикладных проблемах, в которых приходится рассматривать неравенства, часто имеют дело с весом, объемом и т. п., с модулем или абсолютной величиной таких математических объектов, как действительные числа, комплексные числа, векторы. Все эти величины измеряются неотрицательными числами. Так, если даже условиться обозначать выигрыши положительными числами, а проигрыши отрицательными числами, то все же будет естественно сказать, что проигрыш в три доллара больше, чем проигрыш в два доллара - и это несмотря на то, что число -3 меньше, чем -2. При этом мы имеем в виду,

что абсолютная величина числа -3 больше абсолютной величины числа -2.

В этой главе мы дадим определение абсолютной величины действительного числа и изучим некоторые ее свойства для применения их к неравенствам в следующих главах. Мы также приведем графики некоторых интересных и достаточно часто встречающихся функций, содержащих абсолютную величину, и изложим некоторые относящиеся к ним новые идеи.

§ 2. Определение

Абсолютная величина действительного числа а, обозначаемая через может быть определена различными способами. Мы здесь рассмотрим некоторые из возможных определений этого понятия.

Определение. Абсолютная величина действительного числа а определяется как число а, если а положительно или равно нулю, и как число , если а отрицательно.

Так, например,

Принципиальная невыгодность только что приведенного определения заключается в том, что оно не подходит для алгебраических преобразований. Так, например (см. теорему 2 настоящей главы), для любых чисел

что можно проверить, рассматривая отдельно различные возможные случаи: числа оба положительны, одно из чисел положительно, а второе отрицательно; оба числа отрицательны; одно из чисел равно нулю, а второе положительно; одно из чисел равно нулю, а второе отрицательно; оба числа равны нулю. Однако предпочтительнее дать единый вывод, охватывающий все случаи и имеющий чисто алгебраический характер; такой вывод будет дан в § 8 после того, как будут приведены различные определения абсолютной величины, эквивалентные данному выше определению. Эти новые определения будут основываться на понятиях квадрата числа и квадратного корня из числа.

Приведенное выше определение абсолютной величины можно перефразировать следующим образом:

Абсолютная величина действительного числа а равна 0, если во всех же остальных случаях есть положительный элемент множества .

Так, если то есть положительный элемент множества т.е. 2. Если то есть положительный элемент множества т. е. снова 2. Однако этой характеристике символа присущи те же неудобства, что и предыдущей.

§ 3. Специальные символы

Последующие два определения числа связаны с двумя специальными символами: Значение этих символов мы сейчас и объясним.

Символ обозначает наибольший элемент множества действительных чисел.

Если множество содержит только один или только два элемента, мы все же будем говорить о "наибольшем" из его элементов. Если наибольшее значение имеют несколько элементов множества, то любой из них считается наибольшим. Так,

После некоторой тренировки можно научиться производить те или иные арифметические операции над выражениями, содержащими символ

Так, например,

В частности, рассмотрим если то

и т. д. Таким образом, для любых а

так что соотношение (3.1) можно принять за еще одно определение

Перейдем теперь ко второму специальному символу. Символ обозначает наибольший элемент множества если по крайней мере один из его элементов неотрицателен; если же все элементы множества отрицательны, то этот: символ означает число 0. Так,

Как и в случае символа можно производить арифметические действия с выражениями, содержащими символ хотя это и представляет известные неудобства. Так, например,

Как показывают рассмотренные примеры, символы не эквивалентны. Действительно, легко можно видеть, что

Отсюда следует, что

причем знак равенства имеет место тогда и только тогда, когда множество содержит по крайней мере один неотрицательный элемент.

А так как множество при любом значении а содержит неотрицательный элемент, то при любом значении а

Таким образом, равенство

также можно рассматривать как определение величины

Упражнения

(см. скан)

(см. скан)

§ 4. Графические рассмотрения

Графическое изображение может дать поразительно яркую картину поведения функции независимо от того, имеем ли мы дело со средней суточной температурой, колебаниями рынка сбыта, величиной или с чем-нибудь еще. Самым важным здесь является то, что график позволяет нам с одного взгляда усмотреть некоторые общие свойства функции, которые при иных способах ее изучения могли бы остаться скрытыми.

Например, значение символов становится более понятным при рассмотрении изображенных на рис. 2 и 3 графиков функций

Пунктирными линиями на рис. 2 и 3 продолжены графики функций

Построим теперь график функции который дает наглядную характеристику понятия абсолютной величины. Для наших целей достаточно ограничиться неполным графиком, отвечающим интервалу

Рис. 2. График функции

Рис. 3. График функции

При построении этого графика сначала полезно и интересно рассмотреть график функции т. е. множество упорядоченных пар действительных чисел где а также график функции Эти графики изображены на рис. 4 и 5. Из этих графиков и определения

сразу следует, что график функции совпадает с графиком как это показано на рис. 6. Мы должны выбирать на рис. 4 и 5 большую из ординат отвечающих данной абсциссе Эта большая

ордината и служит ординатой у на графике, изображенном на рис. 6. Например, при большей ординатой будет при большей ординатой будет

Рис. 4. График функции

Рис. 5. График функции

На рис. 7 изображен график функции Рассматривая четыре графика, изображенные на рис. 4-7, мы заметим, что для любого значения абсциссы все четыре ординаты не меньше - и не больше

Рис. 6. График функции

Рис. 7. График функции

Поэтому из рис. 4, 6 и 7 можно сделать следующий вывод, который вы, безусловно, смогли бы заметить и доказать вообще без рассмотрения графиков:

Теорема 1. Для каждого действительного числа а

При этом первый знак равенства имеет место тогда и только тогда, когда а второй - тогда и только тогда, когда .

В экономической науке статистические дисциплины находятся на приоритетных позициях. Это обусловлено различными причинами. В первую очередь в рамках общеэкономических специальностей статистические исследования выступают в качестве основы разработки и совершенствования аналитических методов. Кроме этого, они являются самостоятельным направлением, имеющим собственный предмет.

Абсолютные и относительные величины

Эти понятия выступают как ключевые элементы в статистической науке. Они используются для определения количественных характеристик, динамики их изменения. Абсолютные и относительные величины отражают разные характеристики, но без одних не могут существовать другие. Первые выражают количественные размеры того или иного явления безотносительно к другим. По ним нельзя оценить происходящие изменения и отклонения. Они выражают объем и уровень процесса или явления. Абсолютные величина являются всегда именованными числами. Они имеют размерность или единицу измерения. Они могут быть натуральными, трудовыми, денежными и проч. К примеру, нормо-часы, шт., тыс. руб. и так далее. Средние и относительные величины, наоборот, выражают соотношение нескольких точных размеров. Оно может устанавливаться для нескольких явлений или для одного, но взятого в другом объеме и в иной период. Эти элементы выступают как частное от статистических чисел, которое характеризует количественное их соотношение. Чтобы определить относительные величины, нужно один размер разделить на другой, принятый в качестве базового. Последними могут быть плановые данные, фактические сведения предыдущих лет или другого предприятия и так далее. Относительная может выражаться в процентах (при базе, принятой за 100) или коэффициентах (если база единица).

Классификация статистических чисел

Абсолютные величины представлены в двух типах:

1. Индивидуальные. Они характеризуют размер признака у конкретных единиц. Например, это может быть величина зарплаты сотрудника, вклада в банке и так далее. Эти размеры находят непосредственно в ходе статистического наблюдения. Они фиксируются в первичной учетной документации.
2. Суммарные. Величины этого типа отражают итоговый показатель признака по совокупности объектов. Эти размеры выступают в качестве суммы количества единиц (численности совокупности) или объема варьирующей характеристики.

Единицы измерения

Натуральные абсолютные величины могут быть простыми. Это, например, тонны, литры, рубли, штуки, километры. Они могут быть и сложными, характеризовать комбинацию нескольких величин. К примеру, в статистике используются тонно-километры для установления грузооборота железнодорожного транспорта, киловатт-часы - для оценки производства электроэнергии и проч. В исследованиях применяются и условно-натуральные единицы. К примеру, тракторный парк может пересчитываться в эталонные машины. Стоимостные единицы применяют для характеристики разнородного товара в денежном выражении. Эта форма, в частности, используется при оценке дохода населения, валового выпуска продукции. Используя стоимостные единицы, статисты принимают во внимание динамику цен во времени, а недостаток преодолевают за счет "сопоставимых" или "неизменных" цен по одному и тому же периоду. Трудовыми величинами учитывают общие затраты работы, трудоемкость тех или иных операций, составляющих технологический цикл. Они выражаются в и проч.

Относительные величины

Основным условием их расчета выступает сопоставимость единиц и наличие реальной связи между исследуемыми явлениями. Та величина, с которой осуществляется сравнение (знаменатель в дроби), выступает, как правило, в качестве базы или основания соотношения. В зависимости от ее выбора, результат может выражаться в различных долях единицы. Это могут быть десятые, сотые (проценты), тысячные (10-я часть % - промилле), десятитысячные (сотая доля % - продецимилле). Сопоставляемые единицы могут являться как одно-, так и разноименными. Во втором случае их наименования формируются от используемых единиц (ц/га, руб./чел. и т. д.).

Виды относительных величин

В статистике используется несколько типов этих единиц. Так, существует относительная величина:

1. Структуры.
2. Планового задания.
3. Интенсивности.
4. Динамики.
5. Координации.
6. Сравнения.
7. Степени экономического развития.

Относительная величина задания выражает отношение запланированного на предстоящий срок к фактически сложившемуся на текущий период. Аналогично рассчитывается единица плана. Относительная величина структуры - это характеристика доли конкретных частей исследуемой совокупности в ее общем объеме. Их расчет осуществляется посредством деления численности в отдельных частях на общее их количество (или объем). Выражаются эти единицы в процентах или простом кратном отношении. К примеру, так рассчитывается удельный вес городского населения.

Динамика

Относительная величина отражает в этом случае отношение уровня объекта в конкретный период к его статусу в прошедшее время. Другими словами, характеризуется изменение явления в течение какого-либо срока. Относительная величина, характеризующая динамику, именуется Выбор базы при расчете осуществляется в зависимости от цели исследования.

Интенсивность

Относительная величина может отражать степень развития какого-либо явления в конкретной среде. В этом случае говорят об интенсивности. Их вычисление производится сравнением разноименных величин, которые находятся в связи друг с другом. Они устанавливаются, как правило, в расчете на 1000, 100 и так далее единиц исследуемой совокупности. Например, на 100 га земли, на тысячу человек и проч. Эти показатели относительных величин - именованные числа. Например, так рассчитывается плотность населения. Она выражается средним числом граждан на 1 кв. км территории. В качестве подтипа таких единиц выступают характеристики степени экономического развития. К ним, например, относят такие виды относительных величин, как уровень ВНП, ВВП, ВИД и проч. на душу населения. Эти характеристики играют важную роль при анализе экономической ситуации в стране.

Координация

Значение относительных величин может характеризовать пропорциональность отдельных элементов целого друг к другу. Расчет осуществляется путем деления одной части на другую. Относительные величины в этом случае выступают как подтип единиц интенсивности. Разница заключается в том, что они отражают уровень распространения разнородных частей одной совокупности. Базой может выступать тот или иной признак, в зависимости от поставленной цели. В этой связи для одного и того же целого можно вычислить несколько относительных величин координации.

Сопоставление

Относительные величины сравнения - это единицы, которые представляют собой частные от деления одноименных статистических признаков, выступающих характеристиками для разных объектов, но относящихся к одному моменту или периоду. К примеру, вычисляется соотношение уровня себестоимости конкретного типа продукции, произведенной двумя предприятиями, производительность труда для разных отраслей и так далее.

Экономическая оценка

В этом исследовании активно используются абсолютные и относительные единицы. Первые применяются для установления соотношения запасов и расходов с источниками финансирования и оценки предприятия по уровню денежной устойчивости. Относительные показатели отражают структуру фондов с состоянием основных и оборотных средств. При экономической оценке используется горизонтальный анализ. В качестве наиболее обобщающей абсолютной величины, характеризующей финансовую устойчивость фирмы, выступает недостаток или излишек источников финансирования затрат и запасов. Расчет производится путем вычитания. Результатом является разница размера источников (за минусом внеоборотных активов), средствами которых формируются запасы, и их количеством. Ключевыми элементами в этом служат следующие статистические единицы:

1. Собственные оборотные активы.
2. Общий показатель плановых источников.
3. Долгосрочные заемные и собственные средства.

Детерминированное факторное исследование

Этот анализ представляет собой определенную методику изучения воздействия факторов, взаимодействие которых с результатами обладает функциональным характером. Это исследование проводится созданием и оценкой В этом анализе достаточно широко применяются относительные показатели. В большинстве случаев в факторном анализе используются мультипликативные модели. К примеру, прибыль можно выразить произведением количества товаров на стоимость единицы. Часть анализа в этом случае ведется 2 способами:

1. предполагает цепную подстановку. Изменение результата за счет фактора вычисляется как произведение отклонения изучаемого признака на базу другого по выбранной последовательности.
2. Метод относительных разниц используется при измерении воздействия факторов на прирост результата. Он применяется тогда, когда в исходных данных присутствуют ранее вычисленные отклонения в процентах.

Динамические ряды

Они представляют собой изменение числовых показателей общественных явлений в течение времени. В качестве одного из важнейших направлений в этом анализе выступает исследование особенностей развития событий за конкретные периоды. Среди них:

Заключение

Несомненно, относительные величины обладают высокой научной ценностью. Однако на практике их нельзя использовать обособленно. Они всегда находятся во взаимосвязи с абсолютными показателями, выражая соотношения последних. Если это не учитывать, то невозможно точно охарактеризовать исследуемые явления. Используя относительные величины, нужно показать, какие конкретно абсолютные единицы скрыты за ними. Иначе можно сделать неверные выводы. Только комплексное использование относительных и абсолютных величин может выступать в качестве важнейшего средства информации и анализа при изучении разнообразных явлений, происходящих в социально-экономической жизни. В целом переход к вычислению отклонений позволяет сопоставлять хозяйственный потенциал и результат деятельности предприятий, которые значительно отличаются по объему используемых ресурсов или иным характеристикам. Относительные величины, кроме того, могут сгладить некоторые процессы (форс-мажор, инфляцию и прочие), которые могут исказить абсолютные единицы в финансовой отчетности.