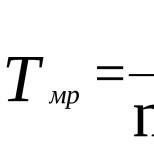Коэффициент корреляции знаков фехнера. Коэффициенты корреляции рангов спирмена, кендалла, коэффициент фехнера
Задача 1. По условным данным таблицы о стоимости основных фондов х
и валовом выпуске продукции у
(в порядке возрастания стоимости основных фондов) выявить наличие и характер корреляционной связи между признаками x
и y
.
Таблица. Стоимость основных фондов и валовой выпуск по 10 однотипным предприятиям
| Предприятия i |
Основные производственные |
Валовой выпуск |
||
1 |
12 |
28 |
– |
– |
Решение.
Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд
методов
. 1. Графический метод
,
когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n
взаимосвязанных пар значений x
и y
и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x
и y
. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии
(см. рисунок справа). Анализируя эту линию, визуально можно определить характер зависимости между признаками x
и y
. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции.
1. Графический метод
,
когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n
взаимосвязанных пар значений x
и y
и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x
и y
. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии
(см. рисунок справа). Анализируя эту линию, визуально можно определить характер зависимости между признаками x
и y
. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции.
2. Рассмотрение параллельных данных
(значений x
и y
в каждой из n
единиц). Единицы наблюдения располагают по возрастанию значений факторного признака х
и затем сравнивают с ним (визуально) поведение результативного признака у
. В нашей задаче в большинстве случаев по мере увеличения значений x
увеличиваются и значения y
(за несколькими исключениями – 2 и 3, 6 и 7 предприятия), поэтому, можно говорить о прямой связи между х
и у
(этот вывод подтверждает и эмпирическая линия регрессии). Теперь необходимо ее измерить, для чего рассчитывают несколько коэффициентов.
3. Коэффициент корреляции знаков (Фехнера
)
– простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x
и y
) от своей средней величины. При этом во внимание принимаются не величины отклонений () и (), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С
) и несовпадений (Н
). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:![]() .
.
Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ=
1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ=–
1(обратная связь). Если же å
С=
å
Н
, то КФ=
0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до 1. Однако, если КФ=
1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х
и у
.
В нашей задаче ![]() ;
; ![]() .
.
В двух последних столбцах таблицы приведены знаки отклонений каждого х
и у
от своей средней величины.
Число совпадений знаков – 9, а несовпадений – 1. Отсюда КФ==0,8 .
Обычно такое значение показателя тесноты связи характеризует сильную зависимость, однако, следует иметь в виду, что поскольку КФ
зависит только от знаков и не учитывает величину самих отклонений х
и у
от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
4.
Линейный коэффициент корреляции
применяется в случае линейной зависимости между двумя количественными признаками x
и y
. В отличие от КФ в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t
:
и .
Линейный коэффициент корреляции r
представляет собой среднюю величину из произведений нормированных отклонений для x
и у
: , или
, или  .
.
Числитель формулы, деленный на n
, т.е. ![]() , представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией
. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х
и у
на произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например:
, представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией
. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х
и у
на произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например:
.
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения.
Например, если , то r по формуле будет положительным, что характеризует прямую зависимость между х и у , в противном случае (r < 0) – обратную связь.
Если , то r
=
0, что означает отсутствие линейной зависимости между х
и у
, а при r
=
1 – функциональная зависимость между х
и у
. Следовательно, всякое промежуточное значение r
от 0 до 1 характеризует степень приближения корреляционной связи между х
и у
к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х
и у
к линейной. Поэтому близость значения r
к 0 в одних случаях может означать отсутствие связи между х
и у
, а в других свидетельствовать о том, что зависимость не линейная.
В нашей задаче для расчета r
построим вспомогательную таблицу.
Таблица. Вспомогательные расчеты линейного коэффициента корреляции
| i | |||||||||
В нашей задаче: = =29,299; ==65,436.
Тогда r = 9,516166/10 = 0,9516.
Аналогично: r = 1824,4/(29,299*65,436) = 0,9516
или r
= (7024,4 – 52*100) / (29,299*65,436) = 0,9516, то есть связь между величиной основных фондов и валовым выпуском продукции очень близка к функциональной.
Проверка коэффициента корреляции на значимость (существенность).
Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x
и y
, на основе которых он рассчитан. Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того, чтобы оценить существенность (значимость) самого r
и, соответственно, реальность измеряемой связи между х
и у
, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σ
r
. Оценка существенности (значимости) r
основана на сопоставлении значения r
с его средней квадратической ошибкой: .
Существуют некоторые особенности расчета σ
r
в зависимости от числа наблюдений (объема выборки) – n
.
- Если число наблюдений достаточно велико (n >30), то σ r рассчитывается по формуле (86):
.
Обычно, если >3, то r
считается значимым (существенным), а связь – реальной.
Задавшись определенной вероятностью, можно определить доверительные пределы (границы)
r = (), где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. таблицу 4).
- Если число наблюдений небольшое (n <30), то σ r рассчитывается по формуле:
,
а значимость r
проверяется на основе t
-
критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (88) и сопоставляется c t
ТАБЛ
.![]() .
.
Табличное значение t
ТАБЛ
находится по таблице распределения t
-критерия Стьюдента (см. приложение 2) при уровне значимости α=1-β
и числе степеней свободы ν=
n
–2
. Если t
РАСЧ
>
t
ТАБЛ
,то r
считается значимым, а связь между х
и у
– реальной. В противном случае (t
РАСЧ
<
t
ТАБЛ
) считается, что связь между х
и у
отсутствует, и значение r
, отличное от нуля, получено случайно.
В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам:
![]() = 0,3073/2,8284 = 0,1086; = 0,9516/0,1086 = 8,7591.
= 0,3073/2,8284 = 0,1086; = 0,9516/0,1086 = 8,7591.
При вероятности 95% t
табл
=
2,306, а при вероятности 99% t
табл
=
3,355, значит, t
РАСЧ
>
t
ТАБЛ
, что дает возможность считать линейный коэффициент корреляции r
= 0,9516 значимым.
5.
Подбор уравнения регрессии
представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у
при том или ином значении факторного признака х,
если остальные факторы, влияющие на у
и не связанные с х,
не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у
со значениями факторного признака х.
Уравнение регрессии можно также назвать теоретической линией регрессии.
Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими
.Они обычно обозначаются (читается: «игрек, выравненный по х»)
и рассматриваются как функция от х
, т.е. =
f
(x
).
(Иногда для простоты записи вместо пишут .
)
Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х
и у, -
одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей.
Для аналитической связи между х
и у
могут использоваться следующие простые виды уравнений:
– прямая линия; ![]() – парабола;
– парабола;
– гипербола; – показательная функция;
– логарифмическая функция и др.
Обычно зависимость, выражаемую уравнением прямой, называют линейной
(или прямолинейной),
а все остальные - криволинейными зависимостями
.
Выбрав тип функции, по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака были бы максимально близки к эмпирическим данным.
Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов
(МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.![]() .
.
Поставив данное условие, легко определить, при каких значениях , и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в методических указаниях к теме 4 «Ряды динамики», поэтому, воспользуемся формулой (57) для нахождения параметров теоретической линии регрессии в нашей задаче, заменив параметр t
на x
. 
Исходные данные и все расчеты необходимых сумм представим в таблице:
Таблица. Вспомогательные расчеты для решения задачи
| i | |||||||
5; x
и y
и измерить тесноту этой связи: коэффициент Фехнера и линейный коэффициент корреляции. |
Следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации.
Он основан на сравнении поведения отклонений индивидуальных значений каждого признака ( и ) от своей средней величины. При этом во внимание принимаются не величины отклонений ![]() , а их знаки («+» или «-»). Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений () и несовпадений ().
, а их знаки («+» или «-»). Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений () и несовпадений ().
Коэффициент Фехнера ()рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:
![]() . (9.12)
. (9.12)
Очевидно, что если знаки всех отклонений по каждому признаку совпадают, то и тогда . Это характеризует наличие прямой связи. Если все знаки не совпадают, то , а , что характеризует обратную связь. Коэффициент Фехнера, как и любой другой показатель тесноты связи, может принимать значения от -1 до +1.
Пример 9.3 . Имеются следующие данные о росте восьми пар братьев и сестер (таблица 9.2).
Таблица 9.2 - Данные о росте восьми пар братьев и сестер
| Рост брата, см | Рост сестры, см |
Определить тесноту зависимости между ростом братьев и сестер на основе:
а) коэффициента Фехнера;
б) коэффициентов корреляции рангов Спирмэна и Кендэла.
Решение:
а) Рассчитаем средние величины и :
Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений () и несовпадений ():
![]() .
.
Коэффициент Фехнера ()рассчитывается по формуле 9.8:
![]() .
.
По величине коэффициента Фехнера () можно сделать вывод о весьма тесной зависимости между и .
б) По уже имеющимся данным (графы 1-2 таблицы 9.2) для нахождения коэффициентов корреляции рангов Спирмэна и Кендэла построим таблицу 9.3.
Таблица 9.3 – Расчетные значения, необходимые для исчисления коэффициентов корреляции рангов Спирмэна и Кендэла
| Подсчет баллов | |||||||
| «+» | «-» | ||||||
| 6,5 6,5 | 1,5 1,5 6,5 6,5 | -0,5 -1 -2 2,5 -0,5 -1,5 | 0,25 6,25 0,25 2,25 | - | - | ||
В данном примере отдельные значения и повторяются. При ранжировании повторяющихся значений, им присваивается ранг, рассчитанный как средняя арифметическая из суммы мест, которые они занимают по возрастанию.
Расчет рангов показан в графах 3 и 4.
Для случая повторяющихся рангов есть особые скорректированные формулы и для коэффициента Спирмэна, и для коэффициента Кендэла. Однако на практике часто пользуются приведенной ранее формулой Спирмэна и для случая повторяющихся рангов, поскольку ошибку она дает весьма малую:
 .
.
Формула коэффициента Кендэла для повторяющихся рангов имеет вид:
 ,
,
где , как и раньше, a и -показатели, корректирующие максимальную сумму баллов и определяемые по формуле , где - число повторяющихся рангов в соответствующем ряду и :
Так как значения рангов идут строго в возрастающем порядке, то следим лишь за поведением . После первой пары значений рангов, где в шести случаях идут значения и ни одного случая, где . Это означает, что в графу 7 мы ставим число «6», а в графу 8число «0». Далее после второй пары значений рангов, где в четырех случаях идут значения и ни одного случая, где . Это означает, что в графу 7 мы ставим число «4», а в графу 8число «0». ». В случае, если бы после второй пары значений рангов, где в трех случаях шли бы значения и два случая, где - это означало бы, что в графу 7 мы ставим число «3», а в графу 8число «2» и т.д.
Расчет и показан в графах 7 и 8. По результатам подсчетов .
Отсюда коэффициент корреляции рангов Кендэла:
По величине коэффициента () можно сделать вывод о весьма тесной зависимости между и , т.е. рост сестры весьма зависим от роста её брата.
Говоря о расчете коэффициента Кендэла, следует еще раз подчеркнуть, что если наблюдаемые единицы совокупности записаны неупорядоченно по одному из признаков (таблица 9.2.), то после ранжирования значений и , ранги одного из признаков, например , следует переписать, расположив их строго в порядке возрастания (или убывания), а для второго признака сохранить значения рангов, соответствующие значениям каждого в исходных данных (таблица 9.3).
Коэффициент конкордации
Корреляция рангов ()может определяться не только для двух, но и для большего числа показателей (факторов). Исчисляемый в этом случае показатель именуется коэффициентом конкордации ()и рассчитывается по формуле:
 , (9.13)
, (9.13)
где - количество коррелируемых факторов;
Число наблюдений;
- сумма квадратов отклонений суммы рангов по факторам от их средней арифметической, т.е.
а)  или, что по значению тоже самое, (9.14)
или, что по значению тоже самое, (9.14)
б)  где - ранг -го показателя. (9.15)
где - ранг -го показателя. (9.15)
Коэффициент конкордации часто используется в экспертных оценках для определения согласованности мнений экспертов в распределение мест (рангов) между исследуемыми факторами или объектами по их приоритетности.
Пример 9.4. Пусть имеются следующие данные по пяти фирмам (графы 1-4 таблицы 9.4).
Таблица 9.4 – Исходные данные и промежуточные расчеты коэффициентов конкордации
| Фирма | Прибыль, тыс. руб. | Стоимость оборотных средств, млн. руб. | Затраты на 100 руб. продукции, руб. | Ранги факторов | Сумма рангов | Квадрат суммы рангов | ||
| 2,0 2,5 1,8 2,2 2,4 | ||||||||
| Σ |
Определить тесноту зависимости между с помощью коэффициента конкордации.
Решение:
1. Ранжираем каждый и трех показателей (графы 5-7).
2. Находим сумму рангов по каждой строке (графа 8) и общую сумму пяти строк
3. Возводим в квадрат сумму рангов в каждой строке и находим сумму пяти строк (графа 9):
 .
.
4. Находим , используя формулу 9.11:
![]() .
.
5. Рассчитаем коэффициент конкордации:
Учитывая малое значение коэффициента конкордации, можно сказать, что зависимость между рассматриваемыми показателями весьма незначительна.
Существуют и другие коэффициенты для измерения тесноты зависимости (коэффициенты ассоциации и контингенции ; коэффициент взаимной сопряженности Пирсона ; коэффициент Чупрова ), которые применяются достаточно редко.
Непараметрические методы
Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий).
Вместе с тем в статистике применяются также непараметрические методы , с помощью которых устанавливается связь между качественными (атрибутивными) признаками . Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты.
В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками , представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.
Для расчета коэффициента ассоциации строится четырехклеточная корреляционная таблица, которая носит название таблицы «четырех полей» и имеет следующий вид:
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Применительно к таблице «четырех полей» с частотами и коэффициент ассоциации выражается формулой:
 . (9.16)
. (9.16)
Коэффициент ассоциации изменяется от -1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой изучаемые признаки.
Если не менее 0,3, то это свидетельствует о наличии связи между качественными признаками.
Пример 9.5 . Имеющиеся данные о росте отцов и сыновей представлены в таблице 9.5.
Таблица 9.5 - Распределение отцов и сыновей по росту, чел.
| Рост сына | Рост отца | Всего | |
| Ниже среднего | Выше среднего | ||
| Ниже среднего | |||
| Выше среднего | |||
| Итого |
Подсчитаем коэффициент ассоциации по данным таблицы 9.5:
![]()
Поскольку , между ростом отцов и сыновей существует корреляционная связь.
Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателя взаимной сопряженности А.A. Чупрова:
 (9.17)
(9.17)
где - число возможных значений первой статистической величины (число групп по столбцам);
Число возможных значений второй статистической величины (число групп по строкам);
Показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки).
Вычтя из этой суммы единицу, получим .
Коэффициент взаимной сопряженности А.А. Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков.
Пример 9.6. Данные об уровне образования членов 100 семей приведены в таблице 9.6.
Таблица 9.6- Распределение семей по уровню образования мужа и жены
Примечание: частоты - верхние строки; их квадраты (в скобках) - средние строки; квадраты частот, деленные на суммы частот по столбцу - нижние строки; в итоговых столбцах - сумма частот, сумма результатов деления (А), а также результат деления нижнего числа на верхнее - последний столбец (В).
Тогда ![]() , .
, .
Коэффициент взаимной сопряженности А.А. Чупрова:
 .
.
Его значение показывает заметную связь между уровнями образования мужа и жены при формировании семьи.
Коэффициент
корреляции, предложенный во II–й
половине XIX
века Г. Т. Фехнером, является наиболее
простой мерой связи между двумя
переменными. Он основан на сопоставлении
двух психологических признаков x
i
и y
i
,
измеренных на одной и той же выборке,
по сопоставлению знаков отклонений
индивидуальных значений от среднего:
и .
Вывод о корреляции между двумя переменными
делается на основании подсчета числа
совпадений и несовпадений этих знаков.
.
Вывод о корреляции между двумя переменными
делается на основании подсчета числа
совпадений и несовпадений этих знаков.
Пример
Пусть x i и y i – два признака, измеренные на одной и той же выборке испытуемых. Для вычисления коэффициента Фехнера необходимо вычислить средние значения для каждого признака, а также для каждого значения переменной – знак отклонения от среднего (табл. 8.1):
Таблица 8.1
|
x i |
y i |
|
|
Обозначение |
|
В таблице: а – совпадения знаков, b – несовпадения знаков; n a – число совпадений, n b – число несовпадений (в данном случае n a = 4, n b = 6).
Коэффициент корреляции Фехнера вычисляется по формуле:
 (8.1)
(8.1)
В рассматриваемом случае:

Вывод
Между исследуемыми переменными существует слабая отрицательная связь.
Необходимо отметить, что коэффициент корреляции Фехнера не является достаточно строгим критерием, поэтому его можно использовать лишь на начальном этапе обработки данных и для формулировки предварительных выводов.
8. 4. Коэффициент корреляции Пирсона
Исходный принцип коэффициента корреляции Пирсона – использование произведения моментов (отклонений значения переменной от среднего значения):
Если сумма произведений моментов велика и положительна, то х и у связаны прямой зависимостью; если сумма велика и отрицательна, то х и у сильно связаны обратной зависимостью; наконец, в случае отсутствия связи между x и у сумма произведений моментов близка к нулю.
Для того чтобы статистика не зависела от объема выборки, берется не сумма произведений моментов, а среднее значение. Однако деление производится не на объем выборки, а на число степеней свободы n - 1.
Величина
 является мерой связи междух
и у
и называется ковариацией х
и у
.
является мерой связи междух
и у
и называется ковариацией х
и у
.
Во многих задачах естественных и технических наук ковариация является вполне удовлетворительной мерой связи. Ее недостатком является то, что диапазон ее значений не фиксирован, т. е. она может варьировать в неопределенных пределах.
Для того чтобы стандартизировать меру связи, необходимо избавить ковариацию от влияния стандартных отклонений. Для этого надо разделить S xy на s x и s y:
 (8.3)
(8.3)
где r xy - коэффициент корреляции, или произведение моментов Пирсона.
Общая формула для вычисления коэффициента корреляции выглядит следующим образом:

 (некоторые преобразования)
(некоторые преобразования)

 (8.4)
(8.4)
Влияние преобразования данных на r xy:
1. Линейные преобразования x и y типа bx + a и dy + c не изменят величину корреляции между x и y .
2. Линейные преобразования x и y при b < 0, d > 0, а также при b > 0 и d < 0 изменяют знак коэффициента корреляции, не меняя его величины.
Достоверность (или, иначе, статистическая значимость) коэффициента корреляции Пирсона может быть определена разными способами:
По таблицам критических значений коэффициентов корреляции Пирсона и Спирмена (см. Приложение, табл. XIII). Если полученное в расчетах значение r xy превышает критическое (табличное) значение для данной выборки, коэффициент Пирсона считается статистически значимым. Число степеней свободы в данном случае соответствует n – 2, где n – число пар сравниваемых значений (объем выборки).
По таблице XV Приложений, которая озаглавлена «Количество пар значений, необходимое для статистической значимости коэффициента корреляции». В данном случае необходимо ориентироваться на коэффициент корреляции, полученный в вычислениях. Он считается статистически значимым, если объем выборки равен или превышает табличное число пар значений для данного коэффициента.
По коэффициенту Стьюдента, который вычисляется как отношение коэффициента корреляции к его ошибке:
 (8.5)
(8.5)
 Ошибка
коэффициента корреляции
вычисляется по
следующей формуле:
Ошибка
коэффициента корреляции
вычисляется по
следующей формуле:
где m r - ошибка коэффициента корреляции, r - коэффициент корреляции; n - число сравниваемых пар.
Рассмотрим порядок вычислений и определение статистической значимости коэффициента корреляции Пирсона на примере решения следующей задачи.
Условие задачи
22 старшеклассника были протестированы по двум тестам: УСК (уровень субъективного контроля) и МкУ (мотивация к успеху). Получены следующие результаты (табл. 8.2):
Таблица 8.2
|
УСК (x i ) |
МкУ (y i ) |
УСК (x i ) |
МкУ (y i ) |
||
Задание
Проверить гипотезу о том, что для людей с высоким уровнем интернальности (балл УСК) характерен высокий уровень мотивации к успеху.
Решение
1. Используем коэффициент корреляции Пирсона в следующей модификации (см. формулу 8.4):

Для удобства обработки данных на микрокалькуляторе (в случае отсутствия необходимой компьютерной программы) рекомендуется оформление промежуточной рабочей таблицы следующего вида (табл. 8.3):
Таблица 8.3
|
x i y i |
||||
|
x 1 y 1 x 2 y 2 x 3 y 3 x n y n |
||||
|
Σx i y i |
2. Проводим вычисления и подставляем значения в формулу:

3. Определяем статистическую значимость коэффициента корреляции Пирсона тремя способами:
1-й способ:
В табл. XIII Приложений находим критические значения коэффициента для 1-го и 2-го уровней значимости: r кр. = 0,42; 0,54 (ν = n – 2 = 20).
Делаем вывод о том, r xy > r кр . , т. е. корреляция является статистически значимой для обоих уровней.
2-й способ:
Воспользуемся табл. XV, в которой определяем число пар значений (число испытуемых), достаточное для статистической значимости коэффициента корреляции Пирсона, равного 0,58: для 1-го, 2-го и 3-го уровней значимости оно составляет, соответственно, 12, 18 и 28.
Отсюда мы делаем вывод о том, что коэффициент корреляции является значимым для 1-го и 2-го уровня, но «не дотягивает» до 3-го уровня значимости.
3-й способ:
Вычисляем ошибку коэффициента корреляции и коэффициент Стьюдента как отношение коэффициента Пирсона к ошибке:
В табл. X находим стандартные значения коэффициента Стьюдента для 1-го, 2-го и 3-го уровней значимости при числе степеней свободы ν = n – 2 = 20: t кр. = 2,09; 2,85; 3,85.
Общий вывод
Корреляция между показателями тестов УСК и МкУ является статистически значимой для 1-го и 2-го уровней значимости.
Примечание:
При интерпретации коэффициента корреляции Пирсона необходимо учитывать следующие моменты:
Коэффициент Пирсона может использоваться для различных шкал (шкала отношений, интервальная или порядковая) за исключением дихотомической шкалы.
Корреляционная связь далеко не всегда означает связь причинно-следственную. Другими словами, если мы нашли, предположим, положительную корреляцию между ростом и весом у группы испытуемых, то это вовсе не означает, что рост зависит от веса или наоборот (оба этих признака зависят от третьей (внешней) переменной, каковая в данном случае связана с генетическими конституциональными особенностями человека).
r xu » 0 может наблюдаться не только при отсутствии связи между x и y , но и в случае сильной нелинейной связи (рис. 8.2 а). В данном случае отрицательная и положительная корреляции уравновешиваются и в результате создается иллюзия отсутствия связи.
r xy может быть достаточно мал, если сильная связь между х и у наблюдается в более узком диапазоне значений, чем исследуемый (рис. 8.2 б).
Объединение выборок с различными средними значениями может создавать иллюзию достаточно высокой корреляции (рис. 8.2 в).
y i y i y i
|
+ + . . |
x i x i x i
Рис. 8.2. Возможные источники ошибок при интерпретации величины коэффициента корреляции (объяснения в тексте (пункты 3 – 5 примечания))
Общее представление о корреляционно-регрессивном анализе
Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.
Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.
Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0. Она используется далее в примерах по теме.
Линейная корреляция
Данная корреляция характеризует линейную взаимосвязь в вариациях переменных. Она может быть парной (две коррелирующие переменные) или множественной (более двух переменных), прямой или обратной — положительной или отрицательной, когда переменные варьируют соответственно в одинаковых или разных направлениях.
Если переменные — количественные и равноценные в своих независимых наблюдениях при их общем количестве , то важнейшими эмпирическими мерами тесноты их линейной взаимосвязи являются коэффициент прямой корреляции знаков австрийского психолога Г.Т.Фехнера (1801-1887) и коэффициенты парной, чистой (частной) и множественной (совокупной) корреляции английского статистика-биометрика К.Пирсона (1857-1936).
Коэффициент парной корреляции знаков Фехнера определяет согласованность направлений в индивидуальных отклонениях переменных и от своих средних и . Он равен отношению разности сумм совпадающих () и несовпадающих () пар знаков в отклонениях и к сумме этих сумм:
![]()
Величина Кф
изменяется от -1 до +1. Суммирование в (1) производится по наблюдениям, которые не указаны в суммах ради упрощения. Если какое-то одно отклонение или , то оно не входит в расчет. Если же сразу оба отклонения нулевые: , то такой случай считается совпадающим по знакам и входит в состав . В таблице 12.1. показана подготовка данных для расчета (1).
|
Число работников, тыс. чел. |
Товарооборот, у.е. |
Отклонение от средних |
Сравнение знаков и |
|||
|
совпа-дение |
несов-падение (Н к) |
|||||
По (1) имеем К ф = (3 — 2)/(3 + 2) = 0,20 . Направление взаимосвязи в вариациях!!Средняя численность работников|численности работников]] и — положительное (прямолинейное): знаки в отклонениях и и в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока — слабая.
Коэффициенты парной, чистой (частной) и множественной (совокупной) линейной корреляции Пирсона, в отличие от коэффициента Фехнера, учитывают не только знаки, но и величины отклонений переменных. Для их расчета используют разные методы. Так, согласно методу прямого счета по несгруппированным данным, коэффициент парной корреляции Пирсона имеет вид:
Этот коэффициент также изменяется от -1 до +1. При наличии нескольких переменных рассчитывается коэффициент множественной (совокупной) линейной корреляции Пирсона. Для трех переменных x, y, z он имеет вид
Этот коэффициент изменяется от 0 до 1. Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние на и , то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:
Этот коэффициент изменяется от -1 до +1. Квадраты коэффициентов корреляции (2)-(4) называются коэффициентами (индексами) детерминации — соответственно парной, чистой (частной), множественной (совокупной):

Каждый из коэффициентов детерминации изменяется от 0 до 1 и оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной (y), обусловленную вариацией другой (других) — x и y. Многомерный случай наличия более трех переменных здесь не рассматривается.
Согласно разработкам английского статистика Р.Э. Фишера (1890-1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании -распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости и имеющейся степени свободы , где — число связей (факторных переменных). Для парного коэффициента имеем его среднеквадратическую ошибку и фактическое значение -критерия Стьюдента:

Для чистого коэффициента корреляции при расчете его вместо (n-2) надо брать , т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.
Если t r > t табл. , то коэффициент парной корреляции — общий или чистый является статистически значимым, а при t r ≤ t табл. — незначимым.
Значимость коэффициента множественной корреляции R проверяется по F — критерию Фишера путем расчета его фактического значения

При F R > F табл. коэффициент R считается значимым с заданным уровнем значимости a и имеющихся степенях свободы и , а при F r ≤ F табл — незначимым.
В совокупностях большого объема n > 100 для оценки значимости всех коэффициентов Пирсона вместо критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).
Наконец, если коэффициенты Пирсона не подчиняются нормальному закону, то в качестве критерия их значимости используется Z — критерий Фишера, который здесь не рассматривается.
Условный пример расчета (2) — (7)дан в табл. 12.2, где взяты исходные данные табл.12.1 с добавлением к ним третьей переменной z — размера общей площади магазина (в 100 кв. м).
Таблица 12.2. Подготовка данных для расчета коэффициентов корреляции Пирсона
|
Показатели |
|||||||||
Согласно (2) — (5), коэффициенты линейной корреляции Пирсона равны:

Взаимосвязь переменных x и y является положительной, но не тесной, составляя по их парному коэффициенту корреляции величину и по чистому — величину и оценивалась по шкале Чеддока соответственно как "заметная" и "слабая".
Коэффициенты детерминации d xy =0,354 и d xy . z = 0,0037 свидетельствуют, что вариация у (товарооборота) обусловлена линейной вариацией x (численности работников) на 35,4% в их общей взаимосвязи и в чистой взаимосвязи — только на 0,37% . Такое положение обусловлено значительным влиянием на x и y третьей переменной z — занимаемой магазинами общей площади. Теснота ее взаимосвязи с ними составляет соответственно r xz =0,677 и r yz =0,844 .
Коэффициент множественной (совокупной) корреляции трех переменных показывает, что теснота линейной взаимосвязи x и z c y составляет величину R = 0,844 , оцениваясь по шкале Чеддока как "высокая", а коэффициент множественный детерминации — величину D=0,713 , свидетельствуя, что 71,3 % всей вариации у (товарооборота) обусловлены совокупным воздействием на нее переменных x и z . Остальные 28,7% обусловлены воздействием на y других факторов или же криволинейной связью переменных y, x, z .
Для оценки значимости коэффициентов корреляции возьмем уровень значимости . По исходным данным имеем степени свободы для и для . По теоретической таблице находим соответственно t табл.1. = 3,182 и t табл.2. = 4,303. Для F-критерия имеем и и по таблице находим F табл. = 19,0. Фактические значения каждого критерия по (6) и (7) равны:

Все расчетные критерии меньше своих табличных значений: все коэффициенты корреляции Пирсона статистически незначимы.
Коэффициент Фехнера - это оценка степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от средних значений факторного и результативного признаков. Коэффициент Фехнера наряду с такими коэффициентами, как коэффициент Спирмэна и коэффициент Кэндэла, относится к коэффициентам корреляции знаков .Назначение сервиса . Данный сервис предназначен для расчета коэффициент Фехнера в онлайн режиме. Также определяется значимость данного коэффициента (см. пример решения).
Инструкция . Укажите количество данных (количество строк), нажмите Далее. Полученное решение сохраняется в файле Word . Также автоматически создается шаблон для проверки решения в Excel .
Расчет коэффициента Фехнера состоит из следующих этапов:
- Определяют средние значения для каждого признака (X и Y).
- Определяют знаки отклонения (-,+) от среднего значения каждого из признаков.
- Если знаки совпадают, присваивают значение А, иначе В.
- Считают количество А и В, вычисляя коэффициент Фехнера по формуле: K ф = (n a - n b)/(n a + n b) где n a - число совпадений знаков отклонений индивидуальных величин от средней; n b - число несовпадений.
Графическое представление коэффициента Фехнера
Пример . При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).
| X1 | 9 | 9 | 11 | 9 | 8 | 11 | 10 | 8 | 10 |
| X2 | 10 | 11 | 10 | 12 | 11 | 12 | 12 | 10 | 9 |