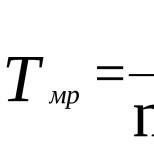Алгоритм джонсона решение задачи о двух станках. Использование алгоритма муравья для решения задачи коммивояжера
1. Рассматриваются интервалы времени и , определяется величина .
2. Если эта величина находится в столбце , то -ю деталь помещаем на первый станок в первую очередь. Если эта величина находится в столбце , то -я деталь занимает последнее место на первом станке.
3. Вычеркиваем выбранную деталь, и продолжаем процедуру поиска, повторяя шаги 1 и 2. В случае одинаковых значений выбираем любую деталь. Полученная последовательность обработки деталей будет оптимальной.
Пример. Пусть время обработки пяти деталей на двух машинах задана в таблице:
Рисунок 6.2 – Начальное расписание
По графику видно, что начальный порядок обработки деталей допускает простои второго станка (суммарное время простоев 8 единиц), длина производственного цикла равна 30 единицам времени.
По алгоритму Джонсона определим величину . В нашем примере эта величина равна . Таким образом, деталь 2 на первом станке обрабатывается последней.
Продолжаем процедуру поиска. Среди не вычеркнутых элементов ищем . После выбора второй детали минимальное время равно 3, и оно соответствует и . Мы можем выбрать любую деталь, поэтому произвольно выбираем , т. е. помещаем на первое место деталь 1. Теперь минимальное время соответствует . Следовательно, деталь 4 ставится на предпоследнее место.
Следующая минимальная величина равна 4 ( и ). Можем назначить 2-е место на первом станке для детали 3 и 3-е место для детали 5.
| i | a i | b i | i¢ |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Полученная последовательность обработки деталей на двух станка =(1, 3, 5, 4, 2) будет оптимальной.
Эта последовательность представлена диаграммой Ганта на рис.6.3.
 |
Рисунок 6.3 – Оптимальное расписание
Из рис. 6. 3 видно, что время обработки всех деталей равно 28 единиц и суммарное время простоев - 6 единиц.
Замечание. Алгоритм Джонсона применим для последовательности деталей, проходящих последовательную обработку на 3-х станках, в двух нижеследующих случаях:
![]() или
или ![]() .
.
Тогда осуществляется поиск оптимальных строк по суммам
Пример. Пусть операции над деталями задаются сроками выполнения :
| i | a i | b i | c i |
Условие ![]() , например, выполняется. Таким образом, мы имеем:
, например, выполняется. Таким образом, мы имеем:
| i | a i | b i | c i | a i + b i | b i + c i |
и алгоритм Джонсона позволяет выбрать =(4, 2, 3, 1, 5).
Задания для самостоятельной работы
Найти решение задачи Джонсона для двух последовательных приборов. Длительности обслуживания приборами А и В приведены в таблице.
| вариант | Требование время | ||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B | |||||||||||
| t A | |||||||||||
| t B |
ЗАДАЧА О НАЗНАЧЕНИЯХ
Рассмотрим задачу последовательной обработки на двух машинах N различных деталей, если известно время A i и B i обработки i
-й детали на соответствующих машинах. Очевидно, что первая машина будет загружена полностью, но вторая может периодически оказываться в состоянии простоя. Попытаемся найти порядок обработки, минимизирующий время простоя второй машины и тем самым сокращающий общее время обработки деталей.
Если обозначить через X i - время простоя в ожидании i
-й детали, то:
A 1
X 1 + X 2 = max(A 1 + A 2 - B 1 , A 1)
X 1 + X 2 + X 3 = max(A 1 + A 2 +A 3 - B 1 - B 2 , A 1 + A 2 - B 1 , A 1)
∑X i = max(∑A i - ∑B i)
Если обозначить через F(t, A k , B k /k=1..N) - суммарное время обработки N деталей при условии, что вторая машина включается с задержкой t и используется оптимальный порядок обработки, то c учетом принципа оптимальности (независимо от выбора начальной детали порядок выбора последующих должен быть оптимальным) имеем:
F(t, A k , B k /k = 1..N) = min(A i + F(B i + max(t-A i ,0),A k ,B k =1..N,k≠i))
Если после i
-й детали при оптимальном порядке обрабатывается j
-я, то:
F(t, A k , B k /k=1..N) = A i + A j + F(t ij , A k , B k /k=1..N; k≠i,j)
где
t ij = B i + max = B i + B j - A i - A j + max
Если max(A i + A j - B i ,A i) < max(A j + A i - B j , A j), то сначала разумнее обрабатывать j
-ю деталь.
Можно показать, что указанное условие необходимости перестановки эквивалентно условию:
min(A j , B i) < min(A i , B j)
Соответственно ищем среди всех значений A i и B i наименьшее. Если найденное значение совпадает с некоторым A i , то i
-ю деталь ставим на обработку первой; если оно совпадает с некоторым Bi
, то последней. Эту процедуру повторяем для всех остальных деталей.
Пример 1. Пусть информация о времени обработки задана таблицей:
Шаг № 2.
Минимальное из значений равно 3 и соответствует B 2: 2-ая деталь обрабатывается последней.
Шаг № 4.
Минимальное из значений равно 5 и соответствует B 4: 4-ая деталь обрабатывается последней.
Шаг № 6.
Минимальное из значений равно 7 и соответствует B 6: 6-ая деталь обрабатывается последней.
В итоге упорядоченная информация принимает вид:
Время простоя второй машины при первичном порядке равно:
max(2 , 2 + 8 - 3 , 2 + 8 + 4 - 3 - 3 , 2 + 8 + 4 + 9 - 3 - 3 - 6 , 2 + 8 + 4 + 9 + 6 - 3 - 3 - 6 - 5 , 2 + 8 + 4 + 9 + 6 + 9 - 3 - 3 - 6 - 5 - 8) = max(2, 7, 8, 11, 12, 13) = 13
Время простоя при оптимальной перестановке равно:
max(2 , 2 + 4 - 3 , 2 + 4 + 6 - 3 - 6 , 2 + 4 + 6 + 9 - 3 - 6 - 8 , 2 + 4 + 6 + 9 + 9 - 3 - 6 - 8 - 7 , 2 + 4 + 6 + 9 + 9 + 8 - 3 - 6 - 8 - 7 - 5) = max(2, 3, 3, 4, 6, 9) = 9
Пример 2. Пусть информация о времени обработки задана таблицей:
Шаг № 2.
Минимальное из значений равно 3 и соответствует B 1: 1-ая деталь обрабатывается последней.
Шаг № 4.
Минимальное из значений равно 4 и соответствует B 6: 6-ая деталь обрабатывается последней.
Алгоритм Джонсона
Алгоритм Джонсона позволяет найти кратчайшие пути между всеми парами вершин взвешенного ориентированного графа. Данный алгоритм работает, если в графе содержатся ребра с положительным или отрицательным весом, но отсутствуют циклы с отрицательным весом.
Алгоритм
Дан граф с весовой функцией. Если веса всех ребер в графе неотрицательные, можно найти кратчайшие пути между всеми парами вершин, запустив алгоритм Дейкстры один раз для каждой вершины. Если в графе содержатся ребра с отрицательным весом, но отсутствуют циклы с отрицательным весом, можно вычислить новое множество ребер с неотрицательными весами, позволяющее воспользоваться предыдущим методом. Новое множество, состоящее из весов ребер должно удовлетворять следующим свойствам.
· Для всех ребер новый вес.
· Для всех пар вершин путь является кратчайшим путем из вершины в вершину с использованием весовой функции тогда и только тогда, когда -- также кратчайший путь из вершины в вершину с весовой функцией.
Сохранение кратчайших путей
Пусть дан взвешенный ориентированный граф с весовой функцией, и пусть -- произвольная функция, отображающая вершины на действительные числа. Для каждого ребра определим:
Пусть -- произвольный путь из вершины в вершину является кратчайшим путем с весовой функцией тогда и только тогда, когда он является кратчайшим путем с весовой функцией, то есть равенство равносильно равенству Кроме того, граф содержит цикл с отрицательным весом с использованием весовой функции тогда и только тогда, когда он содержит цикл с отрицательным весом с использованием весовой функции.
Изменение веса
1. Для данного графа создадим новый граф, где, для некоторой новой вершины, а.
2. Расширим весовую функцию таким образом, чтобы для всех вершин выполнялось равенство.
Недостатком этого алгоритма является то, что в общем случае работа алгоритма может занять значительное время. /3/
Алгоритм муравья
Главная идея алгоритма муравья (метода муравьиных колоний) состоит в моделировании поведения колонии муравьев, которые способны находить кратчайший путь от муравейника до источника пищи и приспосабливаться к изменяющимся условиям внешней среды, находя новый кратчайший путь, если старый в силу каких-либо обстоятельств оказывается недоступным. При движении муравей откладывает феромон, отмечая свой путь, и эту информацию используют другие муравьи. Таким образом, взаимодействие между агентами (муравьями) происходит посредством непрямой коммуникации. /22/
Если моделировать перемещение муравьев на некотором графе, ребра которого представляют собой пути возможного перемещения муравьев, то помимо положительной обратной связи (откладывания феромона) необходимо моделировать отрицательную обратную связь, т.е. испарение феромона. Наличие отрицательной обратной связи гарантирует, что муравьи будут искать другие пути от колонии до источника пищи, т.е. найденное локально оптимальное решение не будет единственным. Решением задачи будет наиболее обогащенный феромоном путь на ребрах графа, который является оптимальным.
Муравьиные алгоритмы позволяют получить решения многих дискретных комбинаторных задач не хуже вышеперечисленных алгоритмов. Чрезвычайно хорошие результаты муравьиной оптимизации получаются для распределенных систем, параметры которых изменяются во времени. Особенностью муравьиных алгоритмов является не-конвергентность - даже после многих итераций одновременно исследуется множество разных решений, что позволяет не застревать в локальных оптимумах. /4/
В данной работе для решения задачи коммивояжера был выбран алгоритм муравья.
, опубликовавшего алгоритм в 1977 году.Алгоритм
См. также
Напишите отзыв о статье "Алгоритм Джонсона"
Ссылки
Литература
- Томас Х. Кормен и др. Алгоритмы: построение и анализ. - 2-е изд. - М .: Издательский дом «Вильямс» , 2007. - С. 726. - ISBN 5-8459-0857-4 .
- Томас Х. Кормен и др. Алгоритмы: построение и анализ. - 1-е изд. - М .: МЦНМО , 2004. - С. 523. - ISBN 5-900916-37-5 .
|
||||||||||||||||||||||||
Отрывок, характеризующий Алгоритм Джонсона
– Нет, я, кажется, домой поеду…– Как домой, да вы вечер у нас хотели… И то редко стали бывать. А эта моя… – сказал добродушно граф, указывая на Наташу, – только при вас и весела…
– Да, я забыл… Мне непременно надо домой… Дела… – поспешно сказал Пьер.
– Ну так до свидания, – сказал граф, совсем уходя из комнаты.
– Отчего вы уезжаете? Отчего вы расстроены? Отчего?.. – спросила Пьера Наташа, вызывающе глядя ему в глаза.
«Оттого, что я тебя люблю! – хотел он сказать, но он не сказал этого, до слез покраснел и опустил глаза.
– Оттого, что мне лучше реже бывать у вас… Оттого… нет, просто у меня дела.
– Отчего? нет, скажите, – решительно начала было Наташа и вдруг замолчала. Они оба испуганно и смущенно смотрели друг на друга. Он попытался усмехнуться, но не мог: улыбка его выразила страдание, и он молча поцеловал ее руку и вышел.
Пьер решил сам с собою не бывать больше у Ростовых.
Петя, после полученного им решительного отказа, ушел в свою комнату и там, запершись от всех, горько плакал. Все сделали, как будто ничего не заметили, когда он к чаю пришел молчаливый и мрачный, с заплаканными глазами.
На другой день приехал государь. Несколько человек дворовых Ростовых отпросились пойти поглядеть царя. В это утро Петя долго одевался, причесывался и устроивал воротнички так, как у больших. Он хмурился перед зеркалом, делал жесты, пожимал плечами и, наконец, никому не сказавши, надел фуражку и вышел из дома с заднего крыльца, стараясь не быть замеченным. Петя решился идти прямо к тому месту, где был государь, и прямо объяснить какому нибудь камергеру (Пете казалось, что государя всегда окружают камергеры), что он, граф Ростов, несмотря на свою молодость, желает служить отечеству, что молодость не может быть препятствием для преданности и что он готов… Петя, в то время как он собирался, приготовил много прекрасных слов, которые он скажет камергеру.
Петя рассчитывал на успех своего представления государю именно потому, что он ребенок (Петя думал даже, как все удивятся его молодости), а вместе с тем в устройстве своих воротничков, в прическе и в степенной медлительной походке он хотел представить из себя старого человека. Но чем дальше он шел, чем больше он развлекался все прибывающим и прибывающим у Кремля народом, тем больше он забывал соблюдение степенности и медлительности, свойственных взрослым людям. Подходя к Кремлю, он уже стал заботиться о том, чтобы его не затолкали, и решительно, с угрожающим видом выставил по бокам локти. Но в Троицких воротах, несмотря на всю его решительность, люди, которые, вероятно, не знали, с какой патриотической целью он шел в Кремль, так прижали его к стене, что он должен был покориться и остановиться, пока в ворота с гудящим под сводами звуком проезжали экипажи. Около Пети стояла баба с лакеем, два купца и отставной солдат. Постояв несколько времени в воротах, Петя, не дождавшись того, чтобы все экипажи проехали, прежде других хотел тронуться дальше и начал решительно работать локтями; но баба, стоявшая против него, на которую он первую направил свои локти, сердито крикнула на него:
– Что, барчук, толкаешься, видишь – все стоят. Что ж лезть то!
– Так и все полезут, – сказал лакей и, тоже начав работать локтями, затискал Петю в вонючий угол ворот.
Петя отер руками пот, покрывавший его лицо, и поправил размочившиеся от пота воротнички, которые он так хорошо, как у больших, устроил дома.
Петя чувствовал, что он имеет непрезентабельный вид, и боялся, что ежели таким он представится камергерам, то его не допустят до государя. Но оправиться и перейти в другое место не было никакой возможности от тесноты. Один из проезжавших генералов был знакомый Ростовых. Петя хотел просить его помощи, но счел, что это было бы противно мужеству. Когда все экипажи проехали, толпа хлынула и вынесла и Петю на площадь, которая была вся занята народом. Не только по площади, но на откосах, на крышах, везде был народ. Только что Петя очутился на площади, он явственно услыхал наполнявшие весь Кремль звуки колоколов и радостного народного говора.
Одно время на площади было просторнее, но вдруг все головы открылись, все бросилось еще куда то вперед. Петю сдавили так, что он не мог дышать, и все закричало: «Ура! урра! ура!Петя поднимался на цыпочки, толкался, щипался, но ничего не мог видеть, кроме народа вокруг себя.
На всех лицах было одно общее выражение умиления и восторга. Одна купчиха, стоявшая подле Пети, рыдала, и слезы текли у нее из глаз.
– Отец, ангел, батюшка! – приговаривала она, отирая пальцем слезы.
 Общий случай задачи выбора последовательности обработки деталей на двух станках, если детали должны пройти обработку на одном станке, а затем на втором и на станке не может обрабатываться больше одной детали, рассмотрел в 1954 г. С. Джонсон. Метод решения такой задачи называют алгоритмом Джонсона.
Общий случай задачи выбора последовательности обработки деталей на двух станках, если детали должны пройти обработку на одном станке, а затем на втором и на станке не может обрабатываться больше одной детали, рассмотрел в 1954 г. С. Джонсон. Метод решения такой задачи называют алгоритмом Джонсона.
 Рассмотрим участок с двумя агрегатами. Совокупность деталей должна последовательно пройти обработку на первом агрегате, а потом на втором. Между агрегатами отсутствует склад, поэтому занятость второго агрегата задерживает освобождение первого. Требуется выбрать очередность обработки деталей, обеспечивающую меньшее суммарное время занятости участка. Это время рассчитывается от момента начала обработки первой детали на первом агрегате до окончания обработки последней детали на втором агрегате.
Рассмотрим участок с двумя агрегатами. Совокупность деталей должна последовательно пройти обработку на первом агрегате, а потом на втором. Между агрегатами отсутствует склад, поэтому занятость второго агрегата задерживает освобождение первого. Требуется выбрать очередность обработки деталей, обеспечивающую меньшее суммарное время занятости участка. Это время рассчитывается от момента начала обработки первой детали на первом агрегате до окончания обработки последней детали на втором агрегате.
 Очевидным является вывод, что выигрыша во времени можно достигнуть только за счет параллельной работы агрегатов. Длительная занятость первого агрегата, пока второй стоит, так же как и занятость второго, когда первый агрегат уже закончил работу, нерациональны. Отсюда ясно, что на первое место в очередности следует поставить деталь с меньшим временем обработки на первом агрегате. Аналогично на последнее место следует поставить деталь, у которой самое короткое время обработки на втором агрегате. Если это правило распространить на всю совокупность деталей, то получим алгоритм Джонсона.
Очевидным является вывод, что выигрыша во времени можно достигнуть только за счет параллельной работы агрегатов. Длительная занятость первого агрегата, пока второй стоит, так же как и занятость второго, когда первый агрегат уже закончил работу, нерациональны. Отсюда ясно, что на первое место в очередности следует поставить деталь с меньшим временем обработки на первом агрегате. Аналогично на последнее место следует поставить деталь, у которой самое короткое время обработки на втором агрегате. Если это правило распространить на всю совокупность деталей, то получим алгоритм Джонсона.
 Обобщения алгоритма Джонсона Значительно больший практический интерес представляло бы решение задачи, подобной задаче о двух станках, для произвольного количества m станков, на которых должны последовательно пройти обработку п деталей. Анализируя алгоритм Джонсона для задачи о двух станках, можно извлечь из него рекомендации, применимые и к общему случаю последовательной обработки деталей на п танках при произвольном m. Обобщения алгоритма Джонсона: 1. В обработку сначала запускают детали, требующие минимальное время обработки на первом станке в порядке возрастания этого времени. 2. В обработку запускаются сначала детали, требующие максимальное время обработки на последнем станке в порядке убывания этого времени. 3. В обработку запускаются сначала детали, у которых “узкое место” находится дальше от начала процесса обработки (“узким местом” для данной детали называется станок, на котором обработка этой деталей занимает наибольшее время). 4. Обрабатываются вначале детали, у которых суммарное время обработки на всех станках максимальное в порядке убывания этого времени.
Обобщения алгоритма Джонсона Значительно больший практический интерес представляло бы решение задачи, подобной задаче о двух станках, для произвольного количества m станков, на которых должны последовательно пройти обработку п деталей. Анализируя алгоритм Джонсона для задачи о двух станках, можно извлечь из него рекомендации, применимые и к общему случаю последовательной обработки деталей на п танках при произвольном m. Обобщения алгоритма Джонсона: 1. В обработку сначала запускают детали, требующие минимальное время обработки на первом станке в порядке возрастания этого времени. 2. В обработку запускаются сначала детали, требующие максимальное время обработки на последнем станке в порядке убывания этого времени. 3. В обработку запускаются сначала детали, у которых “узкое место” находится дальше от начала процесса обработки (“узким местом” для данной детали называется станок, на котором обработка этой деталей занимает наибольшее время). 4. Обрабатываются вначале детали, у которых суммарное время обработки на всех станках максимальное в порядке убывания этого времени.
 Каждое из вышеописанных обобщений алгоритма Джонсона в определенных условиях имеет свои преимущества и свои недостатки. Каждое из этих правил в определенной степени логично. Применение первого из них способствует скорейшему вовлечению в обработку второго станка. Второе правило позволяет уменьшить конечный простой первого станка. Третье правило способствует наиболее быстрому "проскакиванию" к концу технологической линии тех деталей, для которых обработка на первом станке занимает меньшее время, с тем, чтобы освободить первый станок деталям, для которых он является узким местом. К сожалению, эти правила не совместимы друг с другом: последовательность обработки, найденная с использованием одного из них, не соответствует последовательности, полученной по другим правилам.
Каждое из вышеописанных обобщений алгоритма Джонсона в определенных условиях имеет свои преимущества и свои недостатки. Каждое из этих правил в определенной степени логично. Применение первого из них способствует скорейшему вовлечению в обработку второго станка. Второе правило позволяет уменьшить конечный простой первого станка. Третье правило способствует наиболее быстрому "проскакиванию" к концу технологической линии тех деталей, для которых обработка на первом станке занимает меньшее время, с тем, чтобы освободить первый станок деталям, для которых он является узким местом. К сожалению, эти правила не совместимы друг с другом: последовательность обработки, найденная с использованием одного из них, не соответствует последовательности, полученной по другим правилам.
 Пример решения задачи методом Джонсона Время обработки, мин Станок деталь 1 2 3 4 5 Суммарное время обработки 2 5 10 1 5 8 7 5 1 10 3 5 10 2 3 7 7 4 4 5 9 3 1 10 7 4 8 3 1 4 1 2 9 8 2 8 9 2 6 11 25 29 23 27 30 20 22 36
Пример решения задачи методом Джонсона Время обработки, мин Станок деталь 1 2 3 4 5 Суммарное время обработки 2 5 10 1 5 8 7 5 1 10 3 5 10 2 3 7 7 4 4 5 9 3 1 10 7 4 8 3 1 4 1 2 9 8 2 8 9 2 6 11 25 29 23 27 30 20 22 36
 В результате решения задачи по четырем выше указанным рекомендациям получаем такой порядок запуска деталей в обработку: – по первой рекомендации: 7 -1 -3 -6 -2 -4 -8 -5; – по второй рекомендации: 2 -8 -5 -4 -6 -3 -7 -1; – по третьей рекомендации: 2 -8 -5 -7 -3 -1 -6 -4; – по четвертой рекомендации: 8 -5 -2 -4 -1 -3 -7 -6. Примечание. Если по какой-либо рекомендации две, или больше деталей оказываются равноценными, то для определения их приоритетов следует воспользоваться какой-либо другой рекомендацией. Например, по рекомендациям вторая и восьмая детали равноценны, но по первой рекомендации целесообразно в обработку запустить сначала вторую деталь, т. к. время ее обработки на первом станке меньше, чем у восьмой детали.
В результате решения задачи по четырем выше указанным рекомендациям получаем такой порядок запуска деталей в обработку: – по первой рекомендации: 7 -1 -3 -6 -2 -4 -8 -5; – по второй рекомендации: 2 -8 -5 -4 -6 -3 -7 -1; – по третьей рекомендации: 2 -8 -5 -7 -3 -1 -6 -4; – по четвертой рекомендации: 8 -5 -2 -4 -1 -3 -7 -6. Примечание. Если по какой-либо рекомендации две, или больше деталей оказываются равноценными, то для определения их приоритетов следует воспользоваться какой-либо другой рекомендацией. Например, по рекомендациям вторая и восьмая детали равноценны, но по первой рекомендации целесообразно в обработку запустить сначала вторую деталь, т. к. время ее обработки на первом станке меньше, чем у восьмой детали.
 Для каждой детали найдем сумму мест во всех полученных решениях: первая деталь: (2 + 8 + 6 + 5) = 21; вторая деталь: (5 + 1 + 3) = 10; третья деталь: (3 + 6 + 5 + 6) = 20; четвертая деталь: (6 + 4 + 8 + 4) = 22; пятая деталь: (8 + 3 + 2) = 16; шестая деталь: (4 + 5 + 7 + 8) = 24; седьмая деталь: (1 + 7 + 4 + 7) = 19; восьмая деталь: (7 + 2 + 1) = 12.
Для каждой детали найдем сумму мест во всех полученных решениях: первая деталь: (2 + 8 + 6 + 5) = 21; вторая деталь: (5 + 1 + 3) = 10; третья деталь: (3 + 6 + 5 + 6) = 20; четвертая деталь: (6 + 4 + 8 + 4) = 22; пятая деталь: (8 + 3 + 2) = 16; шестая деталь: (4 + 5 + 7 + 8) = 24; седьмая деталь: (1 + 7 + 4 + 7) = 19; восьмая деталь: (7 + 2 + 1) = 12.
 Расположим детали в порядке возрастания суммы мест: 2– 8– 5– 7– 3– 1– 3– 6. Это и является новым решением. При решении конкретных задач для трех и более станков рекомендуется проанализировать результаты, полученные по каждому из этих правил, и в качестве окончательного варианта выбрать ту последовательность, которая обеспечивает минимум суммарного времени обработки.
Расположим детали в порядке возрастания суммы мест: 2– 8– 5– 7– 3– 1– 3– 6. Это и является новым решением. При решении конкретных задач для трех и более станков рекомендуется проанализировать результаты, полученные по каждому из этих правил, и в качестве окончательного варианта выбрать ту последовательность, которая обеспечивает минимум суммарного времени обработки.