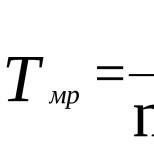Вычисление импульсной характеристики фильтра. Цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры). Фильтр с конечной импульсной характеристикой

>> Экстремумы

Экстремум функции

Определение экстремума

Функция y = f (x ) называется возрастающей (убывающей ) в некотором интервале, если при x 1 < x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) > f (x 2)).

Если дифференцируемая функция y = f (x ) на отрезке возрастает (убывает), то ее производная на этом отрезке f " (x ) > 0

(f " (x ) < 0).

Точка x о называется точкой локального максимума (минимума ) функции f (x ), если существует окрестность точки x о , для всех точек которой верно неравенство f (x ) ≤ f (x о ) (f (x ) ≥ f (x о )).

Точки максимума и минимума называются точками экстремума , а значения функции в этих точках - ее экстремумами.

Точки экстремума

Необходимые условия экстремума . Если точка x о является точкой экстремума функции f (x ), то либо f " (x о ) = 0, либо f (x о ) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x о - критическая точка. Если f " (x ) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.

Второе достаточное условие. Пусть функция f (x ) имеет
f " (x ) в окрестности точки x о и вторую производную в самой точке x о . Если f " (x о ) = 0, >0 ( <0), то точка x о является точкой локального минимума (максимума) функции f (x ). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие .

На отрезке функция y = f (x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .

Пример 3.22.

Решение. Так как f " (

Задачи на нахождения экстремума функции

Пример 3.23. a

Решение. x и y y
0 ≤ x ≤
> 0, а при x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение функции кв . ед ).

Пример 3.24. p ≈

Решение. p p
S "
R = 2, Н = 16/4 = 4.

Пример 3.22. Найти экстремумы функции f (x ) = 2x 3 - 15x 2 + 36x - 14.

Решение. Так как f " (x ) = 6x 2 - 30x +36 = 6(x -2)(x - 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках
x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимум f (2) = 14 и минимум f (3) = 13.

Пример 3.23. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение. Обозначим стороны площадки через x и y . Площадь площадки равна S = xy . Пусть y - это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x + y = a . Поэтому y = a - 2x и S = x (a - 2x), где
0 ≤ x ≤ a /2 (длина и ширина площадки не могут быть отрицательными). S " = a - 4x, a - 4x = 0 при x = a/4, откуда
y = a - 2 × a/4 =a/2. Поскольку x = a /4 - единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x a /4 S " > 0, а при x >a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение функции S(a/4) = a/4(a - a/2) = a 2 /8 (кв . ед ). Поскольку S непрерывна на и ее значения на концах S(0) и S(a /2) равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является y = 2x.

Пример 3.24. Требуется изготовить закрытый цилиндрический бак вместимостью V=16 p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?

Решение. Площадь полной поверхности цилиндра равна S = 2 p R(R+Н). Мы знаем объем цилиндра V = p R 2 Н Þ Н = V/ p R 2 =16 p / p R 2 = 16/ R 2 . Значит, S(R) = 2 p (R 2 +16/R). Находим производную этой функции:
S " (R) = 2 p (2R- 16/R 2) = 4 p (R- 8/R 2). S " (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.

Введение

Цифровой фильтр (ЦФ) - устройство, пропускающее, либо подавляющее заданные в цифровой форме сигналы в определенной полосе частот. В отличие от аналоговых фильтров, у которых входной сигнал изменяется непрерывно, в цифровых фильтрах входной сигнал представляется в дискретной форме, т. е. принимает каждый раз новое значение через интервал дискретизации. Величина, обратная этому интервалу, - частота дискретизации.

Фильтры частотной селекции - это устройства, пропускающие или подавляющие частоты определенного диапазона в составе спектра входного сигнала.

Существует четыре основных типа фильтров частотной селекции: низкочастотный, высокочастотный, полосовой и режекторный.

Цифровой фильтр частотной селекции - это наиболее известный, хорошо изученный и апробированный на практике тип ЦФ.

Выделяют два основных вида ЦФ - фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной импульсной характеристикой (БИХ-фильтры).

КИХ-фильтры обладают некоторыми свойствами, желательными с точки зрения построения фильтров. Например, никогда не возникает вопрос об устойчивости и физической реализуемости фильтров, поскольку КИХ-последовательности гарантируют устойчивость, а при введении соответствующей конечной задержки и реализуемость. Более того, КИХ-последовательности можно выбрать так, чтобы фильтры имели строго линейные фазовые характеристики. Поэтому, используя КИХ-последовательности, можно проектировать фильтры с произвольной амплитудной характеристикой.

В данной работе будет рассмотрено проектирование цифровых КИХ-фильтров с помощью метода частотной выборки.

Цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры)

цифровой фильтр процессор

Термином цифровой фильтр называют аппаратную или программную реализацию математического алгоритма, входом которого является цифровой сигнал, а выходом - другой цифровой сигнал, форма которого и амплитудная и фазовая характеристики сильно модифицированы. Во многих приложениях цифровые фильтры предпочтительнее аналоговых, поскольку они позволяют более точно воплотить амплитудные и фазовые спецификации. Кроме того, для цифровых фильтров нехарактерно присущее аналоговым фильтрам изменение характеристик в зависимости от температуры и напряжения.

Цифровой фильтр можно представить некоторым функциональным блоком, на вход которого поступает входной сигнал x(n) в виде последовательности числовых отсчетов, а с выхода снимаются числовые отсчеты выходного сигнала y(n).

Порядок расчета цифрового фильтра включает четыре основных этапа:

1. Определение требуемых свойств фильтра. На данном этапе задается тип фильтра (ФНЧ, ФВЧ), нужная амплитудная или фазовая характеристика и разрешенные допуски, частота дискретизации и длина слов, которыми будут представлены входные данные.

2. Вычисление коэффициентов. На этом этапе определяются коэффициенты передаточной функции H(z) , которая удовлетворяет заданным свойствам фильтра.

3. Выбор структуры. Данный этап включает преобразование передаточной функции, полученной на предыдущем этапе, в подходящую фильтрующую структуру.

4. Проверка моделированием, удовлетворяет ли полученный фильтр заданным требованиям.

Для того чтобы реализовать цифровой фильтр, необходимо знать его частотную характеристику, передаточную функцию, а для фильтров с конечной импульсной характеристикой достаточно знания отсчетов импульсной характеристики h(n), так как каждый отсчет выходного сигнала может быть вычислен как результат свертки входного сигнала с импульсной характеристикой:

где N - порядок фильтра (длина импульсной характеристики).

Желательно иметь минимальное N, при котором еще удовлетворяются требования к частотной характеристике фильтра. Тогда для реализации фильтра потребуется меньшая вычислительная мощность, т.е. будут меньше затраты времени и памяти.

Существует два основных вида цифровых фильтров: фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной импульсной характеристикой (БИХ-фильтры).

Цифровые КИХ_фильтры обладают рядом достоинств по сравнению с цифровыми фильтрами с бесконечной импульсной характеристикой (БИХ_фильтры). Они всегда устойчивы, менее чувствительны к точности представления числовых параметров фильтра и, главное, могут быть спроектированы таким образом, что их фазочастотная характеристика будет строго линейной, что обычно бывает желательно, а иногда необходимо. Недостатком КИХ_фильтров является то, что для получения частотных характеристик с крутыми перепадами между областями пропускания и задерживания требуются фильтры высоких порядков, т.е. с длинной импульсной характеристикой.

Рассмотрим основные характеристики КИХ-фильтров.

Амплитудно-частотная характеристика КИХ-фильтра часто задается в виде схемы допусков. Такая схема для фильтра нижних частот показана на рисунке. Подобную схему можно получить и для других частотно-избирательных фильтров.

Основные параметры:

дp - отклонение в полосе пропускания (или неравномерность);

дs - отклонение в полосе подавления;

fp - граничная частота полосы пропускания;

fs - граничная частота полосы подавления;

Fs - частота дискретизации.

На практике удобнее выражать дp и дs в децибелах. Расстояние между fs и fp равно ширине полосы перехода фильтра. Другой важный параметр - длина фильтра N , которая определяет число коэффициентов фильтра. В большинстве случаев указанные параметры полностью определяют частотную характеристику КИХ-фильтра.

Линейная фазовая характеристика КИХ-фильтра.

Пусть {h (n)} -- физически реализуемая последовательность конечной длины, заданная на интервале 0. Ее z-преобразование равно:

Преобразование Фурье от {h (n)}:

является периодическим по частоте с периодом 2р.

Из уравнения (3) видно, что модуль преобразования Фурье является симметричной функцией, а фаза --антисимметричной функцией частоты, т.е.

На практике при расчете КИХ-фильтров часто требуется строго линейная фазовая характеристика. При этом фазовая характеристика и(щ) имеет вид:

где б -- постоянная фазовая задержка, выраженная через число интервалов дискретизации.

Условие (7) означает, что для каждого N существует только одна фазовая задержка б, при которой может достигаться строгая линейность фазовой характеристики фильтра. Из условия (8) следует, что при заданном б, удовлетворяющем условию (7), импульсная характеристика должна обладать вполне определенной симметрией.

В зависимости от значения N (нечетные или четные) и вида симметрии импульсной характеристики (симметричная или антисимметричная характеристика) возможны четыре различных вида КИХ-фильтров с линейными фазовыми характеристиками.

Таблица1. Различие четырех типов КИХ-фильтров с линейной фазовой характеристикой

цифровой обработка фильтр шум

Существует два основных типа цифровых фильтров, два программных алгоритма: фильтры с конечной импульсной характеристикой (КИХ) и фильтры с бесконечной импульсной характеристикой (БИХ). Как следует из терминологии, эта классификация относится к импульсным характеристикам фильтров.

КИХ-фильтры

Фильтр с конечной импульсной характеристикой (нерекурсивный фильтр, КИХ-фильтр) - один из видов электронных фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра - некая константа. Изменяя веса коэффициентов и число звеньев КИХ-фильтра, можно реализовать практически любую частотную характеристику. КИХ-фильтры могут иметь такие свойства, которые невозможно достичь методами аналоговой фильтрации (в частности, совершенную линейную фазовую характеристику). Но высокоэффективные КИХ-фильтры строятся с большим числом операций умножения с накоплением и поэтому требуют использования быстрых и эффективных процессоров.

При нулевых значениях коэффициентов am уравнение (2.2) переходит в уравнение линейной дискретной свертки функции x(k) с оператором bn:

y(k) = bn x(k-n). (2.3)

Значения выходных отсчетов свертки (2.3) для любого аргумента k определяются текущим и "прошлыми" значениями входных отсчетов. Такой фильтр и называется нерекурсивным цифровым фильтром (НЦФ). Интервал суммирования по n получил название "окна" фильтра. Окно фильтра составляет N+1 отсчет, фильтр является односторонним каузальным, т.е. причинно обусловленным текущими и "прошлыми" значениями входного сигнала, и выходной сигнал не может опережать входного. Каузальный фильтр может быть реализован физически в реальном масштабе времени. При k

При обработке данных на ЭВМ ограничение по каузальности снимается. В программном распоряжении фильтра могут находиться как "прошлые", так и "будущие" значения входной последовательности отсчетов относительно текущей точки вычислений k, при этом уравнение (2.3) будет иметь вид:

y(k) =bn x(k-n). (2.4)

При N" = N фильтр называется двусторонним симметричным. Симметричные фильтры, в отличие от односторонних фильтров, не изменяют фазы обрабатываемого сигнала.

Реакция НЦФ на единичный входной импульс (а равно и на любой произвольный входной сигнал) всегда конечна и ограничена размером окна фильтра, поэтому такие фильтры и называют фильтрами с конечной импульсной характеристикой (КИХ-фильтры).

Техника выполнения фильтрации не отличается от техники выполнения обычной дискретной свертки двух массивов данных.

Представим, что на одной полоске бумаги выписаны по порядку сверху вниз значения данных x(k) ? sk (см. рис. 6). На второй полоске бумаги находятся записанные в обратном порядке значения коэффициентов фильтра bn ? hn (обозначение h для коэффициентов операторов НЦФ является общепринятым). Для вычисления yk ? y(k) располагаем вторую полоску против первой таким образом, чтобы значение h0 совпало со значением sk, перемножаем все значения hn с расположенными против них значениями sk-n, и суммируем все результаты перемножения. Результат суммирования является выходным значением сигнала yk. Сдвигаем окно фильтра - полоску коэффициентов hk, на один отсчет последовательности sk вниз (или массив sk сдвигаем на отсчет вверх) и вычисляем аналогично следующее значение выходного сигнала, и т.д.

Рис.6.

Описанный процесс является основной операцией цифровой фильтрации, и называется сверткой в вещественной области массива данных с оператором фильтра. Для математического описания наряду с формулами (2.3 и 2.4) применяются символические формы записи фильтрации:

y(k) = b(n) * x(k-n) b(n) ? x(k-n).

Сумма коэффициентов фильтра определяет коэффициент передачи (усиления) средних значений сигнала в окне фильтра и постоянной составляющей в целом по массиву данных (с учетом начальных и конечных условий). Как правило, сумма коэффициентов фильтра нормируется к 1.

Для операции фильтрации характерны следующие основные свойства:

• · Дистрибутивность: h(n) ? = h(n) ? a(k)+h(n) ? b(k).
• · Коммутативность: h(n) ? a(k) ? b(k) = a(k) ? b(k) ? h(n).
• · Ассоциативность: ? h(n) = h(n) ? a(k) ? b(k).

Фильтрация однозначно определяет выходной сигнал y(k) для установленного значения входного сигнала s(k) при известном значении импульсного отклика фильтра h(n).

Имеется целый ряд методов обработки данных, достаточно давно и широко известных, которые по существу относятся к методам цифровой фильтрации, хотя и не называются таковыми. Например, методы сглаживания отсчетов в скользящем окне постоянной длительности. Так, для линейного сглаживания данных по пяти точкам с одинаковыми весовыми коэффициентами используется формула:

yk = 0.2(xk-2+xk-1+xk+xk+1+xk+2).

С позиций цифровой фильтрации это не что иное, как двусторонний симметричный нерекурсивный цифровой фильтр:

yk =bn xk-n, bn = 0,2. (2.5)

Пример: Дано уравнение НЦФ: bn=0.2.

Начальные условия - нулевые.

Входной сигнал - скачок функции (ступень): xk = {0,0,0,0,0,0,10,10,10,10,…}.

Выходной сигнал: yk = {0,0,0,0,2,4, 6, 8,10,10,10,10,…}.

Результат фильтрации приведен на рисунке 7:

КИХ-фильтры обладают рядом полезных свойств, из-за которых они иногда более предпочтительны в использовании, чем БИХ-фильтры. Например:

• 1. КИХ-фильтры устойчивы.
• 2. КИХ-фильтры при реализации не требуют наличия обратной связи.
• 3. Фаза КИХ-фильтров может быть сделана линейной

для n =0, 1, ..., (N /2)–1, когда N четное, и для n =0, 1,..., (N –1)/2, когда N нечет­ное, то цифровой фильтр будет обладать линейной фазовой характеристикой.

В большинстве случаев именно потребность в линейной фазе или постоянном групповом времени вызывает необходимость применения цифровых КИХ-фильтров.

1. Метод частотной выборки.

Заданный уравнением (33) цифровой КИХ-фильтр имеет эквивалентное ДПФ-преобразование вида:

где k =0, 1, 2, …, N –1. Используя непосредственно данные соотношения (38), можно получить подходящую КИХ-передаточную функцию из уравнения (37). Эта методика обеспечивает совпадение полученной и требуемой частотных характеристик в точках дискретизации q =2pk /N для k =0, 1, 2,..., N –l.

2. Метод взвешивания.

Поскольку частотная характеристика Н (е j q ) любого цифрового фильтра представляет собой периодическую функцию частоты q , она имеет разложение в ряд Фурье:

,

(39)

где .

(40)

Очевидно, что коэффициенты ряда Фурье h (n ) фактически представляют собой импульсную характеристику цифрового фильтра.

Одним из возможных способов получения цифровых КИХ-фильтров, аппроксимирующих функцию Н (е j q ), является усечение бесконечного ряда (39) до конечного числа членов. Однако из хорошо известного явления Гиббса следует, что усечение бесконечного ряда вызывает выбросы и колебания в требуемой частотной характеристике до и после любой точки разрыва. Кроме того, величина этих выбросов и колебаний не уменьшается с увеличением длины последовательности при условии сохранения ее конечности. Это по существу означает, что прямое усечение уравнения (39) для получения аппроксимации цифрового КИХ-фильтра не обеспечивает хороших результатов.

Метод взвешивания используется для получения конечных весовых последовательностей w (n ), называемых окнами, которые модифицируют коэффициенты Фурье в уравнении (39) для получения требуемой импульсной характеристики h d (n ) конечной длительности, где:

а w (n ) – последовательность конечной длительности, т. е. w (n )=0 для n >N и n <0. Из соотношения (41) следует, что результирующая импульсная характеристика h d (n ) также имеет протяженность N отсчетов.

Поскольку умножение двух последовательностей во временной области эквивалентно свертке двух частотных характеристик в частотной области, метод взвешивания обеспечивает сглаживание выбросов первоначальной частотной характеристики, т. е. подавление ее отклонений и пульсаций. Недостатком является расширение переходной полосы.

Для завершения этого подраздела приведем некоторые характерные функции окна:

а) прямоугольное окно:

б) окно Бартлетта или треугольное окно:

в) окно Ханна:

Как и в случае аналоговых фильтров, цифровые БИХ-фильтры не могут обеспечить совершенные линейные фазовые характеристики. В противоположность им цифровые КИХ-фильтры могут быть рассчитаны для обеспечения линейных фазовых характеристик. Кроме того, цифровые КИХ-фильтры всегда устойчивы. Это положительные качества цифровых КИХ-фильтров. К отрицательным чертам относится то, что исполнение цифрового КИХ-фильтра требует большего числа вычислений и большего числа цифровых элементов. Однако во многих ситуациях требуются цифровые КИХ-фильтры для выполнения тех задач, которые невозможно решить на основе цифровых БИХ-фильтров, а именно: получение фильтров с линейной фазой и многоскоростных фильтров, где входной и соответствующий выходной сигналы дискретизированы на разных скоростях.

2.3.3 Представление цифровых фильтров на z- плоскости.

Цифровой фильтр может быть синтезирован путем размещения полюсов и нулей передаточной функции на z- плоскости, основанном на следующих правилах:

1. Полюса и нули должны быть либо действительными, либо иметь комплексно-сопряженную пару.

2. Полюс в точке z=0 оказывает влияние на фазо-частотную характеристику фильтра и не изменяет амплитудно-частотную.

3. Полюс (или ноль) на единичной окружности означает, АЧХ на данной частоте бесконечно возрастает (или обращается в ноль).

4. Полюс вне единичной окружности означает, что фильтр нестабилен, т.е. отклик фильтра на импульс не затухает, а возрастает.

Амплитудно-частотная характеристика и представление на z- плоскости цифрового полосовой фильтр 6-го порядка, где:

– ноль, –полюс.

ИЗУЧЕНИЕ СВОЙСТВ И ПАРАМЕТРОВ ЦИФРОВЫХ ФИЛЬТРОВ

Целью работы является генерация сигнала, состоящего из нескольких гармоник, в системе MATLAB 6.1 и исследование в приложении действия фильтров нижних, верхних частот, полосовых и режекторных фильтров на этот сигнал.

Первой задачей является генерация сигнала. Для этого запустите MATLAB 6.1. В начале создания некоторого сигнала зададим вектор-столбец времени t. Для этого в окне Command Window наберите строку:

>> t=(0:.01:2)’;

Эта команда задает изменение t от 0 до 2 с шагом 0,01 и обеспечивает дискретизацию сигнала по времени.

Теперь зададим вектор некоторой функции y(t) , которая представляет собой сумму синусоиды с амплитудой 1 и частотой 1 Гц с синусоидой, имеющей амплитуду 0.25 и частоту 3 Гц:

>> y=sin(2*pi*1*t)+0.25*sin(2*pi*3*t);

Обратите внимание на то, что в этом выражении t – вектор, а потому и y тоже будет вектором. Частота f =1 Гц в первой компоненте сигнала указана в явном виде (как 1) только ради наглядности. Полезно учесть, что в большинстве расчетов MATLAB не использует размерные величины, поэтому лучше сразу привыкнуть к безразмерным величинам.

Теперь можно задать построение графика y(t) :

>> plot(t,y);

Обрабатывать сигналы удобно используя приложение Signal Processing Tool (SPTool) , которое вызывается следующей командой:

Чтобы импортировать сохраненный нами сигнал в это приложение выберите в меню File пункт Import… В раскрывшимся окне поставьте переключатель Source в положение From Workspace . В поле Workspace Contents выберите строку, в которой записано имя функции описывающей сигнал (в данном примере это y ), и нажмите на верхнюю кнопку со стрелкой. В поле Sampling Frequency введите частоту дискретизации. Эта величина обратна шагу изменения времени t , заданному при формировании сигнала (в данном примере шаг изменения t равен 0,01, а частота дискретизации, следовательно, равна 100).

В поле Name записано имя, под которым будет значиться данный сигнал в приложении SPTool . На данной стадии это имя можно изменить по собственному усмотрению. Нажмите кнопку Ok .

Теперь в списке Signals наряду с именами встроенных сигналов появилось имя импортированного сигнала. Нажав кнопку View под списком Signals , можно посмотреть график выделенного сигнала.

В данном приложении можно проектировать и использовать цифровые фильтры для обработки сигналов. В списке Filters записаны имена трех встроенных фильтров. При нажатии кнопки View под списком Filters , появится окно Filter Viever . В нем можно посмотреть:

АЧХ-фильтра (амплитуду можно задать либо в линейном, либо в логарифмическом масштабе либо в децибелах; частоту – либо в линейном, либо в логарифмическом масштабе);

ФЧХ-фильтра (угол можно задать либо в радианах, либо в градусах; частоту – либо в линейном, либо в логарифмическом масштабе);

Групповое время задержки фильтра;

Нули и полюса фильтра;

Отклик на единичный импульс.

Нажав на кнопку New , получаем возможность проектирования фильтров. Кнопка Edit дает возможность редактировать ранее созданные фильтры. В раскрывшемся окне Filter Designer задаются параметры фильтра, производится расчет порядка фильтра и вывод АЧХ.

В поле Sampling Frequency введите частоту дискретизации обрабатываемого сигнала. В поле Algorithm можно выбрать один из следующих видов цифровых фильтров:

КИХ-фильтр Ремеза;

КИХ-фильтр с минимальным среднеквадратическим отклонением;

КИХ-фильтр с окном Кайзера;

БИХ-фильтр с аппроксимацией Баттерворта;

БИХ-фильтр с аппроксимацией Чебышева;

БИХ-фильтр с аппроксимацией инверсной Чебышева;

БИХ-фильтр с эллиптической аппроксимацией.

Выбрав пункт Pole/Zero Editor можно задать с помощью мыши или вводя координаты на Z -плоскости полюса и нули передаточной функции.

Порядок фильтра либо рассчитывается (если стоит птичка в поле Minimum Order ), если вводится в поле Order (если птичка снята). В данной работе порядок фильтров будет рассчитываться.

В поле Type задается тип фильтра: ФНЧ, ФВЧ, полосовой или режекторный фильтр.

Ниже вводятся граничные частоты и затухания полос пропускания и задерживания.

Все вносимые изменения будут тут же отображаться на графике, если поставить птичку в поле Auto Design .

Чтобы отфильтровать сигнал, выберите его в списке Signals , затем в списке Filters выберите фильтр и нажмите на кнопку Apply . В раскрывшимся окне введите (или оставьте введенное по умолчанию) имя отфильтрованного сигнала. Нажмите Ok . Теперь это имя добавилось в списке Signals . Посмотреть график отфильтрованного сигнала можно описанным выше способом.

Задание

1. Сгенерируйте сигнал, состоящий из трех гармоник с частотами 1 , 3, и 5 Гц, имеющих амплитуды 1, 0.5 и 0.75 соответственно. Импортируйте этот сигнал в приложение SPTool и отфильтруйте его так, чтобы:

а) выделить первую гармонику;

б) выделить вторую гармонику;

в) выделить третью гармонику;

г) подавить только вторую гармонику;

используя для этого фильтры нижних, верхних частот, полосовой и режекторный (заградительный) фильтры.

2. Создайте БИХ-фильтр с аппроксимацией Баттерворта. Не меняя параметров фильтра, измените аппроксимацию с Баттерворта на Чебышева, затем на инверсную Чебышева и эллиптическую. Как при этом меняется АЧХ и порядок фильтра.

3. Создайте полосовые БИХ- и КИХ-фильтры с одинаковыми параметрами. Просмотрите АЧХ и ФЧХ данного фильтра. Сравните АЧХ, ФЧХ и порядки полученных фильтров.

4. Сформируйте два синусоидальных сигнала частотой 10 Гц и 20 Гц, длительностью 5 секунд и частотой дискретизации 1000 Гц.

Создайте полосовой БИХ-фильтр с аппроксимацией Чебышева со следующими параметрами:

Частота дискретизации – 1000 Гц;

Левая граничная частота полосы задерживания – 2 Гц;

Левая граничная частота полосы пропускания – 5 Гц;

Правая граничная частота полосы пропускания – 495 Гц;

Правая граничная частота полосы задерживания – 498 Гц;

Максимальное затухание в полосе пропускания – 1дБ;

Минимальное затухание в полосе задерживания – 60дБ.

Создайте полосовой КИХ-фильтр Чебышева (Equiripple FIR ) с аналогичными параметрами.

Отфильтруйте сформированные сигналы с помощью созданных фильтров. Сравните сдвиг фазы между сигналами до фильтрации и после при использовании БИХ- и КИХ-фильтра.

5. С помощью редактора Pole/Zero Editor синтезируйте:

а) фильтр нижних частот;

б) фильтр верхних частот;

в) полосовой фильтр;

г) режекторный (заградительный) фильтр.

6. Запустите приложение Filter Design & Analysis Tool с помощью команды

В данном приложении сформируйте полосовой КИХ-фильтр использую метод взвешенных функций (FIR Window ) со следующими параметрами:

Порядок фильтра – 50;

Частота дискретизации – 2000 Гц;

Левая граничная частота – 250 Гц;

Правая граничная частота – 750 Гц.

Определите использование какой оконной функции дает наибольшее затухание передаточной функции на частоте 200 Гц. Какой минимальный порядок фильтра, передаточная функция которого имеет затухание 40 дБ на частоте 200 Гц?

Контрольные вопросы

1. Назовите 4 основных вида аналоговых фильтров-прототипов.

2. Какие фильтры являются рекурсивными (БИХ), а какие нерекурсивными (КИХ)?

3. Что такое групповое время задержки?

4. Назовите методы расчета БИХ-фильтров.

5. Достоинства и недостатки метода взвешивания при проектировании КИХ-фильтров.

6. Преимущества и недостатки БИХ- и КИХ-фильтров.

7. Как необходимо включать фильтры при создании эквалайзера.