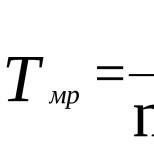Математическое моделирование (дополнительные главы математики) - презентация. Презентация для урока "составление математических моделей" Примеры математических моделей в технологии презентация

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Математические модели

05.05.17 Математические модели Основным языком информационного моделирования в науке является язык математики. Модели, построенные с использованием математических понятий и формул, называются математическими моделями. Математическая модель - информационная модель, в которой параметры и зависимости между ними выражены в математической форме.

05.05.17 Например, известное уравнение S=vt, где S - расстояние, v - скорость t - время, представляет собой модель равномерного движения, выраженную в математической форме.

05.05.17 Рассматривая физическую систему: тело массой m , скатывающееся по наклонной плоскости с ускорением a под воздействием силы F , Ньютон получил соотношение F = mа. Это математическая модель физической системы.

05.05.17 Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятия числа, геометрической фигуры, уравнения, являются примерами математических моделей. К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить математическую модель). Математическое моделирование

05.05.17 При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на языке математики. Пример: нужно определить площадь поверхности стола. Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой. Из всех свойств стола выделили три: форма поверхности (прямоугольник) и длины двух сторон. Не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется. Предположив, что поверхность стола – прямоугольник, легко указать исходные данные и результат. Они связаны соотношением S = ab .

05.05.17 Рассмотрим пример приведения решения конкретной задачи к математической модели. Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Даны некоторые предположения о формах сундука и окнах иллюминатора и исходные данные решения задачи. Предположения: Иллюминатор имеет форму круга. Сундук имеет форму прямоугольного параллелепипеда. Исходные данные: D - диаметр иллюминатора; x - длина сундука; y - ширина сундука; z - высота сундука. Конечный результат: Сообщение: можно или нельзя вытащить.

05.05.17 Если, то сундук можно вытащить, а если, то нельзя. Системный анализ условия задачи выявил связи между размером иллюминатора и размерами сундука, учитывая их формы. Полученная в результате анализа информация отобразилась в формулах и соотношениях между ними, так возникла математическая модель. Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом:

05.05.17 Пример 1: Вычислить количество краски для покрытия пола в спортивном зале. Для решения задачи нужно знать площадь пола. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок. Пусть A – длина пола, B - ширина пола, S 1 - площадь, которую можно покрыть содержимым одной банки, N – количество банок. Площадь пола вычисляем по формуле S = A×B , а количество банок, необходимых для покраски зала, N = A×B / S 1 .

05.05.17 Пример 2: Через первую трубу бассейн наполняется за 30 часов, через вторую трубу – за 20 часов. За сколько часов бассейн наполнится через две трубы? Решение: Обозначим время заполнения бассейна через первую и вторую трубу А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t. Так как через первую трубу бассейн наполняется за А часов, то 1/А –часть бассейна, наполняемая первой трубой за 1 час; 1/В - часть бассейна, наполняемая второй трубой за 1 час. Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/А+1/В. Можно записать: (1/А+1/В) t =1 . получили математическую модель, описывающую процесс наполнения бассейна из двух труб. Искомое время можно вычислить по формуле:

05.05.17 Пример 3: На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А со скоростью 50 км/ч. Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов. За t часов мотоциклист проедет 50 t км и будет находится от А на расстоянии 50 t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой: S=50t + 20 , где t>0 .

05.05.17 Первое число равно x , а второе на 2,5 больше первого. Известно, что 1/5 первого числа равна 1/4 второго. Составьте математические модели данных ситуаций: У Миши x марок, а у Андрея в полтора раз больше. Если Миша отдаст Андрею 8 марок, то у Андрея станет марок вдвое больше, чем останется у Миши. Во втором цехе работают x человек, в первом – в 4 раза больше, чем во втором, а в третьем - на 50 человек больше, чем во втором. Всего в трех цехах завода работают 470 человек. Проверим: Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: б ыло у Миши х марок; у Андрея 1,5х. Стало у Миши х-8 , у Андрея 1,5х+8 . По условию задачи 1,5х+8=2(х-8). Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: во втором цехе работают x человек, в первом – 4х, а в третьем - х+50 . х+4х+х+50=470. Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: первое число х; второе х+2,5 . По условию задачи х/5=(х+2,5)/4.

05.05.17 Вот так обычно применяется математика к реальной жизни. Математические модели бывают не только алгебраические (в виде равенства с переменными, как в разобранных выше примерах), но и в другом виде: табличные, графические и другие. С другими видами моделей мы познакомимся на следующем занятии.

05.05.17 Задание на дом: § 9 (стр. 54-58) № , 2, 4 (стр. 60) в тетради

05.05.17 Спасибо за урок!

05.05.17 Источники Информатика и ИКТ: учебник для 8 класса http://www.lit.msu.ru/ru/new/study (графики, схемы) http://images.yandex.ru (картинки)

Объект (транспортный процесс)

Практические

Расчётная схема

Математическая модель

математическая модель

Алгоритм

Программа

На первом этапе математического моделирования осуществляется переход от объекта моделирования к расчётной схеме. Расчётная схема – это содержательная или (и) концептуальная модель объекта. Например: план перевозки грузов, маршрутная карта, транспортная таблица и т.д.

На втором этапе осуществляется поиск и формализованное описание процесса (процессов) расчётной схемы математической моделью.

На третьем этапе выполняется качественный и количественный анализ математической модели включающий: 1) упрощение, 2) разрешение противоречий, 3) коррекция.

На четвёртом этапе разрабатывается эффективный алгоритм математического моделирования, по которому на пятом этапе создаётся программа для реализации математического моделирования.

На шестом этапе выполняется получение практических рекомендаций путём использования программы. Практические рекомендации – это результат использования математической модели для конкретной цели при исследовании объекта (транспортного процесса).

Цели математического моделирования: 1) создание моделей транспортных процессов для дальнейшего конструирования оптимальных (по времени, по стоимости) транспортных процессов; 2) анализе свойств отдельных транспортных процессов с целью оценки времени и стоимости.

Виды математического моделирования

	Параметрическое			Имитационное
				моделирование
				моделирование

Статическое		Динамическое



			Стационарное		Нестационарное

Параметрическое моделирование – это моделирование без строгой связи с объектом и процессом. Связь осуществляется только параметрами, например: массой, длиной, давлением и т.д. Присутствуют абстракции: материальная точка, идеальный газ и т.д.

Статические параметрические модели не содержат параметра «время» и позволяют получить характеристики системы в равновесии. Динамические параметрические модели содержат параметр время и позволяют получить характер переходных процессов системы.

Имитационное моделирование (Simulation) – математическое моделирование с учётом геометрических особенностей объекта моделирования (размеров, формы) а также распределения плотности с привязкой начальных и граничных условий (условий на границах геометрии объекта) к объектам.

процессов

Программа Алгоритм

Стационарное моделирование позволяет получить характеристики объекта в интервале времени стремящемся к нулю, то есть «сфотографировать» характеристики объекта. Нестационарное моделирование позволяет получить характеристики объекта с течением времени.

Структура математической модели

Входные параметры	Уравнения,	Выходные параметры
	Уравнения,
	зависимости и т.д.

Свойства математической модели:

1)Полнота – степень отражения известных свойств объекта; 2)Точность – порядок совпадения реальных (экспериментальных) и найденных с помощью модели характеристик;

3)Адекватность – это способность модели описывать выходные параметры с фиксированной точностью для фиксированных входных параметров (область адекватности).

4) Экономичность – это оценка затрат вычислительных ресурсов на получение результата по сравнению с аналогичной математической моделью;

5) Робастность – устойчивость математической модели по отношению к погрешностям исходных данных (например данные не соответствуют физике процесса);

6) Продуктивность – это влияние точности входных данных на точность выходных данных модели;

7) Наглядность и простота модели .

Математические модели (по способу получения)

Эмпирические Теоретические

Полуэмпирические © ФГБОУ ВПО УГАТУ; каф. «Прикладная гидромеханика» 16

Эмпирические математические модели получают путём обработки и анализа результатов экспериментальных данных. Идентификация – коррекция существующей математической модели эмпирическими данными.

Теоретические математические модели получают теоретическими методами – анализ, синтез, индукция, дедукция и т.д.

Литература по теории математического моделирования и математическим моделям:

1)Зарубин В. С. Математическое моделирование в технике: учеб. для вузов / В. С. Зарубин. – 3-е изд. – М.: Изд-во МГТУ им. Н.Э. Баумана. 2010. – 495 с.

2)Черепашков А. А., Носов Н. В. Компьютерные технологии, моделирование и автоматизированные системы в машиностроении: Учебн. для студ. высш. учебн. заведений. – Волгоград: Издательский дом «Ин-фолио», 2009. – 640 с.

4. Mathcad как средство прикладного программирования

Mathcad – система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается лёгкостью использования и применения.

Mathcad был задуман и первоначально написан Алленом Раздовом из массачусетского технологического института.

Разработчик: PTC. Первый выпуск: 1986 год.

Решение дифференциальных и алгебраических уравнений численными

методами;
Построение двухмерных и трёхмерных графиков функций;

Использование греческого алфавита;

Выполнение вычислений в символьном виде;

Поддержка собственного языка программирования

© ФГБОУ ВПО УГАТУ; каф. «Прикладная гидромеханика»

Численные функции предназначены для вычисления численными методами прикладной математики корней уравнений, решения задач оптимизации, решения дифференциальных уравнений методом Рунге- Кутта и т.д.

Символьные функции предназначены для аналитических вычислений, которые похожи по своей структуре на классические математические преобразования.

Системная переменная TOL – Допустимая погрешность вычислений (по умолчанию 10-3 ).

Задание ранжированных переменных с фиксированным шагом: x:=0, 0+0.01..10.

Если переменная представляет собой массив, то обратится к элементу массива можно через ввод индекса клавишей [.

«Системный подход в моделировании» - Процесс - динамическое изменение системы во времени. Система - совокупность взаимосвязанных элементов, образующих целостность или единство. Питер Фердинанд Дракер. Системный подход в организациях. Системный подход как основа введения профильного обучения. Основоположники системного подхода: Структура- способ взаимодействия элементов системы посредством определенных связей.

«ISO 20022» - Элементы методологии международного стандарта. Сопоставление состава и свойств. Назначение. Процесс моделирования. Особенности методологии. Результаты моделирования. Открытость и развитие. Миграция. Название Международного стандарта. Аспекты универсальности. Инструментарий. Деятельность. Состав документов.

«Понятие модели и моделирования» - Виды моделей по отраслям знаний. Виды моделей. Основные понятия. Виды моделей в зависимости от времени. Виды моделей в зависимости от внешних размеров. Адекватность моделей. Образно-знаковые модели. Необходимость создания моделей. Моделирование. Модели моделирование.

«Модели и моделирование» - Изменение размеров и пропорций. Математическая модель- модель, представленная на языке математических отношений. Блок-схема- одна из специальных разновидностей графа.. Анализ объекта. Структурная модель- преставление информационной знаковой модели в виде структуры. Реальное явление. Абстрактное. Вербальные.

«Этапы разработки модели» - Описательные информационные модели обычно строятся с использованием естественных языков и рисунков. Построение описательной информационной модели. Основные этапы разработки и исследования моделей на компьютере. 4 этап. 1 этап. 5 этап. Модель солнечной системы. Практическое задание. 3 этап. 2 этап.

«Моделирование как метод познания» - В биологии – классификация животного мира. Определения. Определение. В физике – информационная модель простых механизмов. Моделирование как метод познания. Формы представления информационных моделей. Табличная модель. Процесс построения информационных моделей с помощью формальных языков называется формализацией.

Всего в теме 18 презентаций

Основы математического моделирования

С.В. Звонарев
Основы математического
моделирования
Лекция № 2. Математические модели и их классификации
Екатеринбург
2012

Цель лекции

Определить понятие математической модели.
Изучить обобщенную математическую модель.
Рассмотреть классификацию математических моделей.
2 Математическая модель.
Обобщенная математическая модель.
.
Степень соответствия математической модели объекту.
Классификация математических моделей.
3

Математическая модель

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
4

Математическая модель

Математической моделью называется совокупность уравнений
или других математических соотношений, отражающих основные
свойства изучаемого объекта или явления в рамках принятой
умозрительной
физической
модели
и
особенности
его
взаимодействия с окружающей средой.
Основными свойствами математических моделей являются:
адекватность;
простота.
Процесс формулировки математической модели называется
постановкой задачи.
Математическая модель является математическим аналогом
проектируемого объекта. Степень адекватности ее объекту
определяется постановкой и корректностью решений задачи
проектирования.
5

Математическое моделирование

Математическая модель технического объекта –
совокупность математических уравнений и отношений
между ними, которая адекватно отражает свойства
исследуемого объекта, интересующие исследователя
(инженера).
Математическое моделирование – это идеальное
научное знаковое формальное моделирование, при котором
описание объекта осуществляется на языке математики, а
исследование модели проводится с использованием тех или
иных математических методов.
Методы отыскания экстремума функции многих
переменных с различными ограничениями часто
называются
методами
математического
программирования.
6

Обобщенная математическая модель

Элементы обобщенной математической модели:
множество входных данных (переменные) X,Y;
математический оператор L;
множество выходных данных (переменных) G(X,Y).
7

Входные данные

X – множество варьируемых переменных, которое
образует пространство варьируемых параметров Rx
(пространство поиска), являющееся метрическим с
размерностью
n,
равной
числу
варьируемых
параметров.
Y – множество независимых переменных (константы),
которое образует метрическое пространство входных
данных Ry. В том случае, когда каждый компонент
пространства Ry задается диапазоном возможных
значений,
множество
независимых
переменных
отображается
некоторым
ограниченным
подпространством пространства Ry.
8

Независимые переменные Y

Они определяют среду функционирования объекта, т.е.
внешние
условия,
в
которых
будет
работать
проектируемый объект. К ним могут относиться:
технические параметры объекта, не подлежащие
изменению в процессе проектирования;
физические
возмущения среды,
взаимодействует объект проектирования;
с
которой
тактические параметры, которые должен достигать
объект проектирования.
9

Математические оператор и выходные данные

Математический оператор L – полная система
математических операций, описывающих численные или
логические соотношения между множествами входных и
выходных данных (переменные). Он определяющий
операции над входными данными.
Множество выходных данных (переменных) G(X,Y)
представляет собой совокупность критериальных функций,
включающую (при необходимости) целевую функцию.
Выходные данные рассматриваемой обобщенной модели
образуют метрическое пространство критериальных
показателей RG.
10

Нелинейность математических моделей

Нелинейность математических моделей
‒ нарушение принципа
суперпозиции, т.е. когда любая линейная комбинация решений не
является решением задачи. Таким образом знание о поведении части
объекта еще не гарантирует знания поведения всего объекта.
Большинство
реальных
процессов
и
соответствующих
им
математических моделей не линейны. Линейные же модели отвечают
весьма частным случаям и, как правило, служат лишь первым
приближением к реальности.
Пример – популяционные модели сразу становятся нелинейными,
если принять во внимание ограниченность доступных популяции
ресурсов.
11

Степень соответствия математических моделей объекту

Сложности:
Математическая модель никогда не бывает тождественна
рассматриваемому объекту и не передает всех его свойств и
особенностей.
Математическая модель является приближенным описанием
объекта и носит всегда приближенный характер.
Точность соответствия определяется степенью соответствия,
адекватности модели и объекта. Способы:
Использование эксперимента (практики) для сравнения моделей и
выбора из них наиболее подходящей.
Унификация математических моделей за счет накопления наборов
готовых моделей.
Перенос готовых моделей из одних процессов на другие,
идентичные, аналогичные.
Использование минимального количества приближений и учет
возмущающих воздействий.
12

Классификация математических моделей

КЛАССИФИКАЦИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
13

Классы математических моделей

Математические модели подразделяют на классы в
зависимости от:
сложности объекта моделирования;
оператора модели;
входных и выходных параметров;
цели моделирования;
способа исследования модели;
объектов исследования;
принадлежности модели к иерархическому уровню
описания объекта;
характера отображаемых свойств;
порядка расчета;
использования управления процессом.
14

Классификация по сложности объекта

В
простых
моделях
при
моделировании
не
рассматривается внутреннее строение объекта, не
выделяются
составляющие
его
элементы
или
подпроцессы.
Объект система соответственно более сложная система,
представляющая собой совокупность взаимосвязанных
элементов, обособленная от окружающей среды и
взаимодействующая с ней как целое.
15

Классификация по оператору модели

Математическую
модель
называют
линейной, если оператор обеспечивает
линейную
зависимость
выходных
параметров
от
значений
входных
параметров.
Математическую
модель
называют
нелинейной, если оператор обеспечивает
нелинейную
зависимость
выходных
параметров
от
значений
входных
параметров.
Математическая модель простая, если оператор модели является
алгебраическим
выражением,
отражающим
функциональную
зависимость выходных параметров от входных.
Модель, включающая системы дифференциальных и интегральных
соотношений, называется сложной.
Модель называется алгоритмической когда удается построить
некоторый имитатор поведения и свойств объекта с помощью алгоритма.
16

Классификация по входным и выходным параметрам

Классификация по характеру моделируемого процесса

Детерминированные,
которые
соответствуют
детерминированным процессам, имеющим строго
однозначную связь между физическими величинами,
характеризующими состояние системы в какой-либо
момент
времени.
Детерминированная
модель
позволяет однозначно вычислить и предсказать
значения выходных величин по значениям входных
параметров и управляющих воздействий.
Неопределенные, которые исходят из того, что
изменение определяющих величин происходит
случайным образом, и значения выходных величин
находятся в вероятностном соответствии с входными
величинами и не определяются однозначно.
18

Неопределенные модели

Стохастические – значения всех или отдельных параметров
модели определяются случайными величинами, заданными
плотностями вероятности.
Случайные – значения всех или отдельных параметров модели
устанавливаются случайными величинами, заданными оценками
плотностей вероятности, полученными в результате обработки
ограниченной экспериментальной выборки данных параметров.
Интервальные – значения всех или отдельных параметров
модели описываются интервальными величинами, заданными
интервалом, образованным минимальным и максимально
возможными значениями параметра.
Нечеткие – значения всех или отдельных параметров модели
описываются функциями принадлежности соответствующему
нечеткому множеству.
19

Классификация по отношению к размерности пространства

Одномерные.
Двумерные.
Трехмерные.
Такое деление применимо для моделей, в число
параметров
которых
входят
координаты
пространства.
20

Классификация по отношению ко времени

Статические. Если состояние системы не

статическими. Статическое моделирование
служит для описания состояния объекта в
фиксированный момент времени.
Динамические. Если состояние системы
меняется со временем, то модели называют
динамическими. Динамическое моделирование
служит для исследования объекта во времени.
21

Классификация по виду используемых множеств параметров

Качественные.
Количественные.
Дискретные.
Непрерывные.
Смешанные.
22

Классификация по целям моделирования

Дескриптивные. Целью таких моделей является установление законов
изменения параметров модели. Пример – модель движения ракеты после
старта с поверхности Земли.
Оптимизационные. Подобные модели предназначены для определения
оптимальных с точки зрения некоторого критерия параметров
моделируемого объекта или же для поиска оптимального режима
управления некоторым процессом. Примером подобной модели может
служить моделирование процесса запуска ракеты с поверхности Земли с
целью подъема ее на заданную высоту за минимальное время.
Управленческие. Такие модели применяются для принятия эффективных
управленческих решений в различных областях целенаправленной
23
деятельности человека.

Классификация по методу реализации

Аналитические. Аналитические методы более удобны для
последующего анализа результатов, но применимы лишь для
относительно простых моделей. В случае, если математическая
задача допускает аналитическое решение, то оно считается
предпочтительнее численного.
Алгоритмические. Алгоритмические методы сводятся к
некоторому
алгоритму,
реализующему
вычислительный
24
эксперимент с использованием ЭВМ.

Классификация по объектам исследования

Объекты с высокой степенью информации. если в процессе
моделирования известны полные системы уравнений,
описывающие все стороны моделируемого процесса и все
числовые значения параметров этих уравнений.
Объекты с нулевым уровнем информации. Математическая
модель такого объекта строится на основе статистических
экспериментальных данных.
Объекты с известными основными закономерностями.
Значения констант в математических уравнениях описания
модели устанавливают из опыта.
Объекты, о поведении которых имеются сведения
эмпирического характера. Для них используют методы
физического моделирования с применением математического
планирования эксперимента.
25

Классификация по принадлежности модели к иерархическому уровню описания объекта

Микроуровень
(типовыми
процессами
являются
массообменные,
теплофизические,
гидродинамические).
Моделирование
осуществляется
в
целях
синтеза
технологического процесса для отдельного или нескольких
агрегатов.
Макроуровень. Моделирование процессов, имеющих более
высокий уровень агрегации; модели применяют для синтеза
текущего управления технологическим процессом для одного
агрегата или технологического комплекса в целом.
Метауровень. Моделирование процессов в совокупности
агрегатов и связывающих их материально-энергетических
потоков. Такие модели служат для синтеза технологического
комплекса как единого целого, то есть для синтеза управления
развитием.
26

Классификация по характеру отображаемых свойств модели

Функциональные
модели.
Используются,
для
описания
физических и информационных процессов, протекающих при
функционировании объекта.
Структурные
модели.
Описывают
состав
и
взаимосвязи
элементов системы (процесса, объекта).
27

Классификация по порядку расчета

Прямые. Применяются для определения кинетических,
статических и динамических закономерностей процессов.
Обратные
(инверсионные).
Используются
для
определения значения входных параметров или других
заданных свойств обрабатываемых веществ или
продуктов, а также для определения допустимых
отклонений режимов обработки (задачи оптимизации
процессов и параметров аппаратов).
Индуктивные.
Применяются
для
уточнения
математических уравнений кинетики, статики или
динамики процессов с использованием новых гипотез или
теорий.
28

Классификация по использованию управления процессом

Модели прогноза, или расчетные модели без управления.
Основное назначение этих моделей – дать прогноз о поведении
системы во времени и в пространстве, зная начальное состояние
и информацию о поведении ее на границе. Примеры -модели
распределения тепла, электрического поля, химической
кинетики, гидродинамики.
Оптимизационные модели.
– Стационарные модели. Используются на уровне проектирования
различных
технологических
систем.
Примеры
‒
детерминированные задачи, вся входная информация в которых
является полностью определяемой.
– Нестационарные
модели.
Используются
на
уровне
проектирования, так и, главным образом, для оптимального
управления различными процессами – технологическими,
экономическими и др. В этих задачах некоторые параметры носят
случайный характер или содержат элемент неопределенности.
29 Гипотеза.
Феноменологическая модель.
Приближение.
Упрощение.
Эвристическая модель.
Аналогия.
Мысленный эксперимент.
Демонстрация возможности.
30

Гипотеза

Эти модели представляют собой пробное
описание явления. Если такая модель построена, то
это означает, что она временно признается за истину
и можно сконцентрироваться на других проблемах.
Однако это не может быть точкой в исследованиях, а
только временной паузой: статус модели может быть
только временным.
Примеры:
Модель Солнечной системы по Птолемею.
Модель Коперника (усовершенствованная Кеплером).
Модель атома Резерфорда.
Модель Большого Взрыва.
и д.р.
31

Феноменологическая модель

Данная модель содержит механизм для описания явления.
Однако этот механизм недостаточно убедителен и не может быть
подтвержден имеющимися данными или плохо согласуется с
имеющимися теориями и накопленным знанием об объекте.
Поэтому феноменологические модели имеют статус временных
решений. Роль модели в исследовании может меняться со
временем, может случиться так, что новые данные и теории
подтвердят феноменологические модели и те будут повышены до
статуса гипотезы. Аналогично, новое знание может постепенно
придти в противоречие с моделями-гипотезами первого типа и те
могут быть переведены во второй.
Примеры:
Модель теплорода.
Кварковая модель элементарных частиц.
и д.р.
32

Приближение

Общепринятый прием в случае когда нельзя
решить даже с помощью компьютера уравнения,
описывающие исследуемую систему – использование
приближений. Уравнения заменяются линейными.
Стандартный пример – закон Ома.
33

Упрощение

В данной модели отбрасываются детали, которые
могут заметно и не всегда контролируемо повлиять на
результат.
Примеры:
Применение модели идеального газа к неидеальному.
Уравнение состояния Ван-дер-Ваальса.
Большинство моделей физики твердого тела,
жидкостей и ядерной физики. Путь от микроописания к
свойствам тел (или сред), состоящих из большого числа
частиц, очень длинен. Приходится отбрасывать многие
детали.
34

Эвристическая модель

Эвристическая модель сохраняет лишь качественное
подобие реальности и дает предсказания только «по
порядку величины».
Оно дает простые формулы для коэффициентов
вязкости, диффузии, теплопроводности, согласующиеся
с реальностью по порядку величины. Но при
построении новой физики далеко не сразу получается
модель, дающая хотя бы качественное описание объекта.
Типичный пример – приближение средней длины
свободного пробега в кинетической теории.
35

Аналогия

Данная
модель
впервые
возникла,
когда
взаимодействие в системе нейтрон-протон пытались
объяснить посредством взаимодействия атома
водорода с протоном. Эта аналогия и привела к
заключению, что должны существовать обменные
силы взаимодействия между нейтроном и протоном,
обусловленным переходом электрона между двумя
протонами.
36

Мысленный эксперимент и демонстрация возможности

Мысленный эксперимент – это рассуждения,
которые в конечном итоге приводят к противоречию.
Демонстрация возможности – это тоже мысленные
эксперименты
с
воображаемыми
сущностями,
демонстрирующие,
что
предполагаемое
явление
согласуется с базовыми принципам и внутренне
непротиворечиво. Один из самых знаменитых таких
экспериментов – геометрия Лобачевского.
37

Заключение и выводы

Рассмотрено понятие математической модели.
Изучена обобщенная математическая модель.
Определены понятия: нелинейность математических моделей и степень
соответствия математической модели объекту.
Представлена классификация математических моделей.
38 Самарский, А.А. Математическое моделирование / А.А. Самарский,
А.П. Михайлов. – М.: Наука. Физматлит, 1997.
Тарасевич, Н.Н. Математическое и компьютерное моделирование.
Вводный курс / Н.Н. Тарасевич. – М.: Эдиториал УРСС, 2001.
Введение в математическое моделирование: уч. Пособие / под
редакцией П.В. Трусова. – М.: Университетская книга, Логос, 2007. –
440 с.

1 из 16

Презентация на тему: Математические модели (7 класс)

№ слайда 1

Описание слайда:

№ слайда 2

Описание слайда:

§ 2.4. Математические модели Основным языком информационного моделирования в науке является язык математики. Модели, построенные с использованием математических понятий и формул, называются математическими моделями.Математическая модель - информационная модель, в которой параметры и зависимости между ними выражены в математической форме.

№ слайда 3

Описание слайда:

№ слайда 4

Описание слайда:

№ слайда 5

Описание слайда:

Математическое моделирование Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятия числа, геометрической фигуры, уравнения, являются примерами математических моделей. К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить математическую модель).

№ слайда 6

Описание слайда:

При математическом моделировании исследование объекта осуществляется посредством изучения модели, сформулированной на языке математики.Пример: нужно определить площадь поверхности стола. Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью прямоугольником. Площадь этого прямоугольника и считается искомой. Из всех свойств стола выделили три: форма поверхности (прямоугольник) и длины двух сторон. Не важны ни цвет стола, ни материал, из которого он сделан, ни то, как он используется. Предположив, что поверхность стола – прямоугольник, легко указать исходные данные и результат. Они связаны соотношением S=ab.

№ слайда 7

Описание слайда:

Рассмотрим пример приведения решения конкретной задачи к математической модели. Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Даны некоторые предположения о формах сундука и окнах иллюминатора и исходные данные решения задачи. Предположения:Иллюминатор имеет форму круга. Сундук имеет форму прямоугольного параллелепипеда. Исходные данные: D - диаметр иллюминатора; x - длина сундука; y - ширина сундука; z - высота сундука. Конечный результат: Сообщение: можно или нельзя вытащить.

№ слайда 8

Описание слайда:

Системный анализ условия задачи выявил связи между размером иллюминатора и размерами сундука, учитывая их формы. Полученная в результате анализа информация отобразилась в формулах и соотношениях между ними, так возникла математическая модель.Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом:

№ слайда 9

Описание слайда:

Пример 1:Вычислить количество краски для покрытия пола в спортивном зале. Для решения задачи нужно знать площадь пола. Для выполнения этого задания измеряют длину, ширину пола и вычисляют его площадь. Реальный объект – пол зала – занимается прямоугольником, для которого площадь является произведением длины на ширину. При покупке краски выясняют, какую площадь можно покрыть содержимым одной банки, и вычисляют необходимое количество банок.Пусть A – длина пола, B - ширина пола, S1 - площадь, которую можно покрыть содержимым одной банки, N – количество банок. Площадь пола вычисляем по формуле S=A×B, а количество банок, необходимых для покраски зала, N= A×B/S1.

№ слайда 10

Описание слайда:

Пример 2:Через первую трубу бассейн наполняется за 30 часов, через вторую трубу – за 20 часов. За сколько часов бассейн наполнится через две трубы?Решение:Обозначим время заполнения бассейна через первую и вторую трубу А и В соответственно. Примем за 1 весь объём бассейна, искомое время обозначим через t. Так как через первую трубу бассейн наполняется за А часов, то 1/А –часть бассейна, наполняемая первой трубой за 1 час; 1/В - часть бассейна, наполняемая второй трубой за 1 час.Следовательно, скорость наполнения бассейна первой и второй трубами вместе составит: 1/А+1/В.Можно записать: (1/А+1/В)t=1. получили математическую модель, описывающую процесс наполнения бассейна из двух труб. Искомое время можно вычислить по формуле:

№ слайда 11

Описание слайда:

Пример 3:На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А со скоростью 50 км/ч.Составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.За t часов мотоциклист проедет 50t км и будет находится от А на расстоянии 50t км + 20 км. Если обозначить буквой s расстояние (в километрах) мотоциклиста до пункта А, то зависимость этого расстояния от времени движения можно выразить формулой: S=50t + 20, где t>0.Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: было у Миши х марок; у Андрея 1,5х. Стало у Миши х-8, у Андрея 1,5х+8. По условию задачи 1,5х+8=2(х-8).

№ слайда 12

Описание слайда:

Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: было у Миши х марок; у Андрея 1,5х. Стало у Миши х-8, у Андрея 1,5х+8. По условию задачи 1,5х+8=2(х-8). Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: во втором цехе работают x человек, в первом – 4х, а в третьем - х+50. х+4х+х+50=470. Математической моделью решения этой задачи являются следующие зависимости между исходными данными и результатом: первое число х; второе х+2,5. По условию задачи х/5=(х+2,5)/4.

№ слайда 13

Описание слайда:

Источники Информатика и ИКТ: учебник для 7 классаАвтор: Босова Л. Л. Издательство: БИНОМ. Лаборатория знаний, 2009 Формат: 60x90/16 (в пер.), 229 с., ISBN: 978-5-9963-0092-1http://www.lit.msu.ru/ru/new/study (графики, схемы)http://images.yandex.ru (картинки)