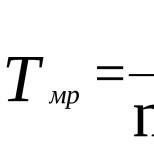Изокванты. Изокванта, ее свойства и виды
Задача любого производителя – минимизировать финансовые потери и добиться максимального объема выпущенной продукции .
Для этого нужно правильно совместить все ресурсы, особенно это касается долгосрочного периода работы, когда внешние факторы постоянно меняются.
С целью решения этой проблемы и были введены новые экономические категории: изокванта, изокоста, изопрофита . Рассмотрим подробно каждую из них.
Что такое изокванта?
Изокванта — это кривая равного выпуска/равного продукта. Она представляет собой линию, соединяющие точки, которыми изображены различные варианты совмещения факторов для поддержания производства продукта на том же уровне.
Предположим, что в компании используются два главных фактора: ресурсы труда и капитала. Тогда изокванта будет выглядеть таким образом (на рис 1. Обозначена Q1):
Рис.1 — График изокванты
Схема, на которой изображены несколько таких линий, получила название карта изоквант.
Свойства изокванты:
Рассмотрим свойства кривых равного продукта (изокванты) :
- Их наклон отрицателен. Принцип построения кривой в том, что в случае меньшего использования капитала затраты трудовых ресурсов возрастают, с целью сохранения производственного объема.
- Кривые равного спроса не пересекаются.
- Большее расстояние изокванты от начала осей означает производство большего количества продукта.
Что означает угловой коэффициент наклона к изокванте?
Угловой коэффициент наклона касательной линии к изокванте – показатель, обозначающий замену производственного фактора другим при выпуске прежнего количества товара. Его численное значение рассчитывают по формуле: MRTS= -K/L. Данный показатель называют предельной нормой технического замещения.
В нашем примере предел нормы замещения – это величина, на которую нужно сократить капитал при включении дополнительных трудовых единиц. При таком замещении труд менее производителен, а капиталовложения используются эффективнее.
Приведенные факторы производитель приобретает на рынке труда, учитывая возможные финансовые затраты и рыночные цены на ресурсы.
Расположение изокванты на графике в различных ситуациях
Рассмотрим ситуации, при которых кривая равного производства выглядит необычно:
- Полная замена одного ресурса другим. Например, выпуск товаров ручной работы или абсолютная автоматизированное производство. Изображение изокванты тогда будет представлять собой наклонную прямую линию, т.к. показатель MRTS в каждой точке неизменяем.
- Использование факторов в строго определенном соотношении. К примеру, в работе землекопа участвует одинаковое число орудий и человек. Увеличивать объем какого-либо ресурса, при том же самом значении другого здесь бессмысленно. Изокванта при таких условиях выглядит как латинская буква L.
Что такое изокоста?
Линия, состоящая из точек, которые показывают разные совокупности применяемых на производстве двух непостоянных факторов, при одинаковой цене на их покупку, носит название изокоста .
Рассмотрим так называемую карту изокост (Рис.2)
 Рис. 2 — Карта изокост
Рис. 2 — Карта изокост
Формула изокосты : С=rK+wL.
С – стоимость производственных факторов, r – затраты на капитал, w – затраты на труд.
Свойства изокосты
Изокосты обладают теми же свойствами, что и линии бюджета:
- Имеют отрицательный наклон;
- Пересекаются с осями;
- Наклонены под определенным углом;
- Вместе с бюджетом производителя изменяются и производственные факторы.
Производителю выгодно подобрать правильное сочетание производственных факторов, которое позволит выпустить установленный объем продукта с наименьшими финансовыми потерями.
Совмещенный график изокост и изоквант
Чтобы верно скомбинировать ресурсы, карты изоквант и изокост совмещаются (Рис 3.)
 Рис. 3 — Совмещенная карта изокосты и изокванты
Рис. 3 — Совмещенная карта изокосты и изокванты
Е на данном графике – точка касания двух линий. Она называется равновесной точкой производства . Именно при этом значении производитель получит минимум издержек при закупке ресурсов. Другие точки изображения (К примеру, А и В) – не оптимальны, ведь они показывают меньший объем выпуска товара при тех же затратах. В точке F же закупка ресурсов вообще невозможна, т.к. она не принадлежит изокосте.
Условие, достигнутое в точке Е графика, называется минимизацией производственных затрат .
Комбинация оптимальных для производства точек, созданная для изменяемых объемов производства и затрат на него, при сохранении стабильной стоимости ресурсов, определяет траекторию развития предприятия. Траектория может быть разной формы и обычно рассматривается в долгосрочном периоде. Она позволяет сделать вывод, является ли выпуск продукции трудоемким либо капиталоемким и подобрать технологии для равномерного применения всех ресурсов.
Вывод: чтобы минимизировать издержки, компании выгодно заменять один производственный фактор другим, пока отношения объемов всех ресурсов к ценам на эти ресурсы не станут равными.
Условия максимизации прибыли
Для поддержания максимизации прибыли в каждой компании должны соблюдаться два важных правила, которые могут быть использованы при любых рыночных условиях :
- У предприятия есть возможность заниматься своей деятельностью, в случае, если его прибыль превышает издержки, при определенном объеме выпуска продукции; и нет, если доход не больше издержек.
- Для получения оптимального объема производства, компанией должен быть выпущен тот объем продукции, при котором максимальный доход равен максимальным издержкам.
Главное условия получения максимально возможного дохода – возможность получать прибыль со всех выпущенных единиц продукции . Для изучения факторов, от которых зависит доход фирмы, применяются такие понятия, как предельный, средний и общий доход.
Обобщенно прибыль можно вычислить, как разность между совокупным доходом и совокупными затратами. Формула: TP=TR-TC.
Уравнение для функции прибыли на производстве с двумя основными ресурсами и одним видом продукта: TP=TR-TC=PQ-(rK+wL).
K здесь – объем капитала, L – количество единиц труда, r – стоимость одной капиталлоединицы, w – стоимость трудовой единицы.
По уравнению функции прибыли можно построить ее график. С этой целью выразим количество выпущенной продукции через величины дохода и затрат:
Q=TP/P+rK/P+wL/P.
Что такое изопрофита?
Предположим, что размер используемого капитала в краткосрочный промежуток времени неизменен. Тогда изображаем на графике зависимость объемов выпуска продукта от переменных значений трудовых единиц. Получаем параллельные наклонные прямые – изопрофиты . (Рис.4) Угол между этими линиями и горизонтальной координатной осью вычисляется по формуле w/P, уравнение для точки пересечения их с вертикалью: TP/P+rK/P.
 Рис. 4 — Изопрофиты
Рис. 4 — Изопрофиты
Другое название изопрофиты – кривая равной прибыли. Это совокупность точек, показывающих сочетание объема выпуска продукта и количества изменяемого ресурса, при которых достигается один уровень дохода.
С помощью функции производства и кривой производства компании несложно выяснить, какой уровень производства и уровень использования ресурсов необходим для получения максимального дохода.
 Рис. 5 — Получение наибольшей прибыли
Рис. 5 — Получение наибольшей прибыли
Рассмотрим Рис.5. На нем видно, что наибольшую прибыль фирма получает в точке пересечения самой высокой изопрофиты с графиком производства.
В долговременном производстве все факторы изменяемы, как и функция дохода. Математически это можно выразить так: функция максимальна, если две первые производные имеют нулевое значение.
Модель олигополии Курно
С помощью изопрофит можно сконструировать модель олигополии Курно. Последняя является вариантом конкуренции на рынке и названа именем французского ученого. Кратко поясним суть этой модели:
- на рынке задействовано определенное число компаний, которые производят один и тот же вид продукции;
- появление на рынке новых предприятий и прекращение деятельности существующих невозможно;
- компании наделены рыночной властью;
- предприятия действуют обособленно и увеличивают свой доход
Число компаний, присутствующих на рынке, должны знать все участники. Каждая из них считает объемы выпуска продукции остальными фирмами неизменной величиной. Значения же затрат могут быть различны.
Дуополия как частный случай
Частным случаем является дуополия (в процессе участвуют две организации). При равновесных условиях каждый дуополист, производя свой товар, на 1/3 реализует потребности рынка. Вместе покрыв спрос на 2/3, участники производства обеспечивают наибольшую прибыль для себя, но не для всей отрасли. Они могли бы добиться максимизации общего дохода, если бы учли свои ошибки в расчетах объемов выпуска продукции друг друга и заключили бы официальное или неофициальное соглашение, образовав монополию. Эта ситуация разделила бы рынок пополам, и каждая компания закрывала бы уже по 1/4 спроса.
Критика модели дуополии Курно
Модель дуополии Курно не раз подвергалась критике, т.к. ее участники делают неправильные предположения о поведении конкурента, нулевыми технические затраты быть не могут, и количество предприятий неизменно, что к равновесию не приводит.
Часть этих минусов может исчезнуть при добавлении в модель Курно кривых реагирования . Но перед этим нужно обратить внимания на кривые равной прибыли – изопрофиты. В указанной модели они представляют собой совокупность точек, показывающих сочетание выпусков обоих дуополистов, при которых одним из участников достигается постоянный уровень прибыли. Для второго дуополиста изопрофита имеет аналогичное значение.
Свойства кривых равной прибыли для дуополии:
- на изопрофите размер прибыли дуополиста неизменен;
- кривые вогнуты к осям участников, каждая из них показывает поведение одного дуополиста относительно второго, с целью сохранения неизменной прибыли;
- большее расстояние кривой от начала координат свидетельствует о меньшем уровне прибыли;
- при любом определенном уровне выпуска одного из дуополистов есть только одно значение этого объема для второго, при котором доход последнего будет максимален;
- соединив максимумы изопрофит каждой фирмы, которые смещены в одну сторону, получаем кривые реагирования.
Кривые реагирования – это совокупности точек наибольшей прибыли, возможной для одного дуополиста, при фиксированном значении выпуска другого.
Таким образом, рынок находится в состоянии равновесия лишь тогда, когда каждое предприятие не меняет своей стратегии в одиночку, а может лишь отвечать на смену поведения на рынке конкурентов.
Изокванта – кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска.
Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Карта изоквант , представляющая собой набор возможных изоквант, показывает все допустимые варианты осуществления производства.
Свойства стандартных изоквант аналогичны характеристикам кривых безразличия:
1. Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек.
2. Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства (изокванты, описывающие данную производственную функцию, никогда не пересекаются).
3. Изокванты не имеют участков возрастания (Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого, так и второго ресурса).
Изокванты строятся на основе эмпирических данных, полученных на основе анализа конкретного производственного процесса, поэтому они несут в себе определенные характеристики этого производства.
Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе, при этом увеличение одного фактора и уменьшение другого не вызывают изменений в объеме выпускаемой продукции.
Положительный наклон изокванты означает увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора.
Крутизна наклона изокванты выражает предельную норму технологического замещения (MRTS), которая измеряется соотношением изменения объема выпуска продукции. Предельная норма технологического замещения трудом капитала (MRTSlk) определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объема выпуска продукции. Предельная норма технического замещения в любой точке изокванты = наклону касательной в этой точке, умноженному на -1:

Поскольку замещение факторов предполагает сохранение объема выпуска, то предельная норма технологического замещения оказывается тесно связанной с предельными продуктами факторов производства. Увеличение труда (∆L) означает рост объема выпуска на Чтобы остаться на той же изокванте, необходимо компенсировать это увеличение за счет сокращения применения капитала на величину ∆K, которая даст сокращение выпуска на Следовательно, чтобы выпуск оставался неизменным должно выполнятся равенство:
Таким образом,  т.е. предельная норма технологического замещения факторов производства = обратному соотношению их предельных продуктов.
т.е. предельная норма технологического замещения факторов производства = обратному соотношению их предельных продуктов.
Данное равенство говорит о том, что в любой точке изокванты предельная норма замещения одного ресурса другим = наклону касательной к точке, лежащей на изокванте.
Свойства стандартных изоквант аналогичны характеристикам кривых безразличия:
1. Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек.
2. Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства (изокванты, описывающие данную производственную функцию, никогда не пересекаются).
3. Изокванты не имеют участков возрастания (Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого, так и второго ресурса).
Предельная норма технологического замещения одного ресурса на другой (например, труда на капитал) показывает степень замещения труда капиталом, при котором объем выпуска остается неизменным.
Алгебраическое выражение, показывающее степень, в которой производитель готов сократить количество капитала в обмен на увеличение труда, достаточную для сохранения прежнего объема выпуска имеет вид: (33)

Рис 30. Предельная норма технологического замещения

Рис. 31. Виды изоквант
Изокванты могут иметь различный вид:
а) линейный – когда предполагается полная за-мещаемость одного фактора другим;
б) в форме угла – когда предполагается жесткая дополняемость ресурсов, вне которой производство невозможно;
в) ломаной кривой, выражающей ограниченную возможность замещения ресурсов;
г) гладкой кривой – наиболее общего случая взаимодействия факторов производства (рис.31).
Изокванта – результат взаимодействия факторов производства. Но в рыночной экономике нет бесплатных факторов. Следовательно, возможности производства не в последнюю очередь лимитируются финансовыми средствами предпринимателя. Роль бюджетной линии в этом случае выполняет изокоста.
Изокоста – линия, ограничивающая комбинацию ресурсов денежными расходами на производство, поэтому ее часто называют линией равных затрат. С ее помощью определяются бюджетные возможности производителя.
Бюджетные ограничения производителя можно рассчитать:
C = r + K + w + L, (34)
где C – бюджетное ограничение производителя; r – цена услуг капитала (часовая арендная плата); K – капитал; w – цена услуг труда (часовая оплата труда); L – труд.
Даже если предприниматель использует не заемные, а собственные средства – это все равно затраты ресурсов, и их следует считать. Соотношение цен факторов r/w показывает наклон изокосты (см. рис 32).

Рис. 32. Изокоста и ее сдвиг
K – капитал; L – труд.
Рост бюджетных возможностей предпринимателя сдвигает изокосту вправо, а снижение – влево. Тот же эффект достигается в условиях неизменности расходов при снижении или росте рыночных цен на ресурсы.
Путем совмещения графиков изокванты и изокосты можно определить равновесие производителя, т. е. тот оптимальный набор ресурсов, который при имеющихся финансовых затратах дает наилучший результат (рис. 33).

Рис. 33. Равновесие производителя
y 1, y 2, y 3 – изокванты; E – точка оптимума.
Отдача от масштаба производства. Величина примененных в производстве факторов составляет масштаб производства.
Отдача от масштаба (т. е. результат производственной деятельности) может быть:
а) постоянной, если результат производства возрастает в той же пропорции, что и ресурсы;
б) убывающей, если результат производства возрастает в меньшей пропорции;
в) возрастающей, если результат производства возрастает в большей пропорции (рис. 34).

Рис. 34. Отдача от масштаба производств
Для упрощения анализа используем две группы факторов производства. Двухфакторная производственная функция
где - капитал, - труд, дает возможность учесть все важные аспекты производства и одновременно дать графический анализ производства. Двухфакторная производственная функция описывается производственной сеткой. Сетка дает возможность определить различные комбинации факторов производства для выпуска определенного объема продукции.
Т.7-1 Производственная сетка
| (L) рабочее время (часы) | (K) Машинное время (часы) | |||
| 100 | 200 | 300 | 400 | |
| 100 | 20 | 30 | 35 | 38 |
| 200 | 30 | 85 | 150 | 210 |
| 300 | 55 | 150 | 210 | 270 |
| 400 | 65 | 180 | 250 | 315 |
| 500 | 72 | 210 | 270 | 320 |
Отобразим графически:
Г.7-1 Карта изоквант
Эти кривые носят название «изокванты».
Изокванта – кривая, отражающая все возможные комбинации факторов производства для выпуска данного объема продукции (для данного выпуска). Изокванта – аналог кривой безразличия.
Карта изоквант – серия изоквант, отражающих комбинации факторов производства (затрат) для достижения разных объемов производства (выпуска).
Свойства изоквант.
Аналогичны свойствам кривых безразличия.
2. Изокванты, принадлежащие одной карте, не пересекаются.
3. Изокванты нисходящие. Уменьшение использования одного фактора (машинное время) требует увеличения другого фактора (рабочего времени).
4. Изокванты выпуклы по отношению к началу координат. Наклон в любой точке определяет норма технологического замещения :
.
Показывает то количество часов работы машины, которое может заместить единица труда при данном объеме выпуска.
уменьшается по мере движения вниз по кривой. Причина – взимодополняемость факторов производства. Каждый фактор может делать то, что не может или делает хуже другой. Они не являются абсолютно взаимозаменяемыми. Следовательно, для замещения каждого дополнительного часа работы машины требуется все большее количество часов труда. То же самое, что сказать: каждый дополнительный час труда может заменить все меньше часов работы машины.
Производственный выбор в краткосрочном периоде
Карта изоквант может быть использована для показа производственного выбора (вариантов оптимального производственного выбора) в рамках краткосрочного периода (не все факторы производства могут меняться).
Пусть . При данной величине объем выпуска может быть изменен путем дополнительного использования труда. Графически, переходя от одной изокванты к другой вдоль линии , переходим от одного объема выпуска к другому.
От степени, в которой изменяются переменные факторы в краткосрочном периоде, зависит увеличение объема выпуска продукции.
Производственная функция графически может быть представлена в виде особой кривой – изокванты.
Изокванта продукта – это кривая, показывающая все сочетания факторов в пределах одного и того же объема производства. По этой причине ее часто называют линией равного выпуска.
Изокванты в производстве выполняют ту же функцию, что и кривые безразличия в потреблении, поэтому они подобны: на графике также имеют отрицательный наклон, обладают определенной пропорцией замещения факторов, не пересекаются между собой и чем дальше расположены от начала координат, тем больший результат производства отражают:
A,b,c,d – различные комбинации; у, y 1 ,у 2 , у 3 – изокванты продукта.
Изокванты могут иметь различный вид:
- линейный – когда предполагается полная за-мещаемость одного фактора другим;
- в форме угла – когда предполагается жесткая дополняемость ресурсов, вне которой производство невозможно;
- ломаной кривой, выражающей ограниченную возможность замещения ресурсов;
- гладкой кривой – наиболее общего случая взаимодействия факторов производства
Сдвиг изокванты возможен под влиянием роста привлекаемых ресурсов, технического прогресса и часто сопровождается изменением ее наклона. Этот наклон всегда определяет предельную норму технического замещения одного фактора другим (MRTS).
 где MRTS– предельная норма технического замещения одного фактора другим.
где MRTS– предельная норма технического замещения одного фактора другим.
Свойства изокванты:
1. Изокванта, так же как и кривая безразличия, является непрерывной функцией, а не набором дискретных точек.
2. Для любого заданного объема выпуска может быть проведена своя изокванта, отражающая различные комбинации экономических ресурсов, обеспечивающих производителю одинаковый объем производства (изокванты, описывающие данную производственную функцию, никогда не пересекаются).
3. Изокванты не имеют участков возрастания (Если бы участок возрастания существовал, то при движении вдоль него увеличивалось бы количество как первого, так и второго ресурса).
Изокоста.
Изокоста – линия, ограничивающая комбинацию ресурсов денежными расходами на производство, поэтому ее часто называют линией равных затрат. С ее помощью определяются бюджетные возможности производителя.
Бюджетные ограничения производителя можно рассчитать:
C = r + K + w + L,
где C– бюджетное ограничение производителя; r– цена услуг капитала (часовая арендная плата); K – капитал; w – цена услуг труда (часовая оплата труда); L– труд.
Даже если предприниматель использует не заемные, а собственные средства – это все равно затраты ресурсов, и их следует считать. Соотношение цен факторов r/w показывает наклон изокосты:

Изокоста и ее сдвиг
K – капитал; L – труд.
Рост бюджетных возможностей предпринимателя сдвигает изокосту вправо, а снижение – влево. Тот же эффект достигается в условиях неизменности расходов при снижении или росте рыночных цен на ресурсы.
Комбинация ресурсов, обеспечивающая минимальный уровень совокупных издержек фирмы, называется оптимальной и лежит в точке касания линий изокосты и изокванты:

34. Понятие оптимума фирмы-производителя.
Производственная функция отражает разные способы соединения факторов для производства определенного объема продукции. Информация, которую несет производственная функция, может быть представлена графически с использованием изоквант.
Изокванта представляет собой кривую, на которой расположены все сочетания производственных факторов, использование которых обеспечивает одинаковый объем выпуска (рис. 11.1).

Рис. 11.1. График изоквант
В долгосрочном периоде, когда фирма может изменить любой фактор производства, производственная функция характеризуется таким показателем, как предельная норма технологического замещения факторов производства (MRTS)
![]() ,
,
где DK и DL – изменения капитала и труда для отдельной изокванты, т.е. для постоянного Q.
Фирма сталкивается с проблемой как достичь определенного объема производства с минимальными издержками. Предположим, что цена труда равна ставке заработной платы (w), а цена капитала равна арендной плате за оборудование (r). Издержки производства можно представить в виде изокост. Изокоста включает все возможные сочетания труда и капитала с равными валовыми издержками

Рис. 11.2. График изокост
Перепишем уравнение валовых издержек, как уравнение для прямой линии, получим
 .
.
Из этого следует, что изокоста имеет угловой коэффициент, равный
Он показывает, что, если фирма отказывается от единицы трудозатрат и экономит w (у.е.), чтобы приобрести единицу капитала по цене r (у.е.) за единицу, то валовые издержки производства остаются неизменными.
Равновесие фирмы возникает тогда, когда она максимизирует прибыль на определенном объеме производства при оптимальном сочетании факторов производства, минимизирующих издержки (рис.11.3).
На графике равновесие фирмы отражает точка касания T изокванты с изокостой при Q 2 . Все другие сочетания факторов производства (A, B) могут дать меньший объем выпуска продукции.

Рис. 11.3. Равновесие потребителя
Учитывая, что в точке Т изокванта и изокоста имеют одинаковый наклон и что наклон изокванты измеряется MRTS, условие равновесия можно представить как
![]() .
.
Правая часть формулы отражает полезность для производителя каждой единицы фактора производства. Эта полезность измеряется предельным продуктом труда (MP L) и капитала (MP К)
Последнее равенство является равновесием производителя. Данное выражение показывает, что производитель находится в равновесии, если 1 рубль, вложенный в единицу труда, равен одному рублю, вложенному в капитал.
35. Понятие отдачи от масштаба.
Эффект масштаба связан с изменением стоимости единицы продукции в зависимости от масштабов её производства фирмой. Рассматривается в долгосрочном периоде. Снижение затрат на единицу продукции при укрупнении производства называется экономией на масштабе . Вид кривой долгосрочных издержек связан с эффектом масштаба производства.
Экономией на масштабе могут воспользоваться компании любого размера, увеличив объем своей операционной деятельности. Наиболее распространёнными методами являются закупки (получение оптовых скидок), менеджмент (используется специализация менеджеров), финансы (получение менее дорогих кредитов), маркетинг (распространение затрат на рекламу для большего ассортимента продукции). Использование любого из этих факторов снижает долгосрочные средние затраты (англ. Long Run Average Costs LRAC ) сдвигая на графике вниз и вправо кривую краткосрочных средних затрат (англ. Short-run average total cost SRATC ).
 Участки производственной кривой с положительной отдачей от масштаба и один (последний) участок - с отрицательной.
Участки производственной кривой с положительной отдачей от масштаба и один (последний) участок - с отрицательной.
Формальное определение
Пусть параметр K - единица капитала, параметр L - единица рабочей силы, параметр a - увеличение/уменьшение в а-раз.
Можно сказать, что для производственной функции при:
положительная отдача от масштаба
постоянная отдача от масштаба
убывающая отдача от масштаба