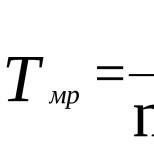Критерии для принятия решения. Статистические игры и принятие решений в условиях неопределенности
Вероятности состояний природы, предполагаемые известными при применении критерия Байеса, могли быть получены из статистических данных, отражающих многократное решение подобных задач, или в результате наблюдений за частотой пребывания природы в том или ином состоянии. Однако довольно часто складываются ситуации, в которых определить вероятности состояний природы нет возможности. Желая все же принять решение о выборе стратегии в условиях риска, оценивают вероятности состояний природы субъективно. Один из субъективных подходов состоит в том, что лицо, принимающее решение, нс может отдать предпочтение ни одному из состояний природы по частоте его наступления и потому считает их равновероятными, т.с. =п~‘,j = 1,2,...,л. Этот принцип называется "принципом недостаточного основания" Лапласа . Па нём основан определяемый ниже критерий Лапласа {If -критерий), представляющий собой частный случай критерия Байеса, когда вероятности состояний задаются указанным образом.
Пусть имеем игру с природой, задаваемой матрицей А (см. (2.5.1)) выигрышей игрока А, а = (, = n~",q 2 =л _|) - вектор вероятностей состояний природы, удовлетворяющих очевидно условиям (2.1.1). Таким образом, в данном случае координаты вектора q зависят от числа состояний природы определенным образом, в то время, как в общем случае зависимость этого вектора от состояний природы состоит только в том, что число его координат равно числу состояний природы.
Из определения критерия Байеса оптимальности чистых стратегий относительно вышрышей получаем следующее определение.
Пьер-Симон Лаплас (23.03.1749 - 05.03.1827)
Критерием Лапласа относительно выигрышей (V’ - критерием) называется критерий, но которому:
- показателем (W -показателем) эффективности чистой стратегии А , (/ = 1,2,...,от) назовем среднее арифметическое выигрышей при этой стратегии, т.с. величину
- ценой (II -ценой) игры в чистых стратегиях назовем наибольший из показателей эффективности (2.7.1):
- оптимальной (II -оптимальной) во множестве чистых стратегий назовем стратегию A k eS L с максимальным показателем эффективности
Из (2.7.2) и (2.7.3) следует, что оптимальность стратегии A k эквивалентна равенству 1!’ к = /,((. Поскольку в правой части формулы (2.7.1) множитель п~" инвариантен относительно номера стратегии, то эффективность стратегий по И - критерию можно характеризовать просто суммами > « = 1,2,...,т. Таким образом, чистая стратегия А к будет II -оптимальной во множестве чистых стратегий, если сумма выигрышей в А-й строке матрицы выигрышей будет максимальной.
Множество стратегий, V" -оптимальных во множестве чистых стратегий, обозначим (s c)° {LP) .
Поскольку критерий Лапласа сеть частный случай критерия Байеса, то все предложения, сформулированные в § 2.5 о критерии Байеса, будут справсдливыми и для критерия Лапласа при замене в них вектора q = (q x ,q 2 ,...,q n) вектором q = (q l =n~",q 2 =n~...,q ll =n~").
Из оценок (2.5.5) и (2.5.6) для показателя эффективности Ц’ и цены игры L p c соответственно получаем:
Необходимость многократного принятия решения о выборе стратегии приводит к использованию смешанных стратегий, оптимальность которых определяется по критерию Лапласа.
Из определения В 1 ’(q) -критерия оптимальности смешанных стратегий относительно выигрышей в частности получаем следующее определение.
По IP -критерию относительно выигрышей
- показателем (L p -показателем) эффективности смешанной стратегии Р = (р 1 ,р 2 ,...,р т) назовем среднее арифметическое вышрышей (2.2.3):
- ценой (L" -ценой) игры в смешанных стратегиях назовем наибольший из показателей эффективности (2.7.6):
- оптимальной (U’ -оптимальной) во множестве смешанных стратегий назовем стратегию Р° =(р“,/>?,...,/?") с наибольшим показателем эффективности:
Из равенств (2.7.7) и (2.7.8) следует, что для любой смешанной оптимальной стратегии справедливо равенство
Из теоремы 2.5.1 вытекает следующая теорема.
Теорема 2.7Л. В любой игре с природой существует стратегия, оптимальная во множестве смешанных стратегий по критерию Лапласа относительно выигрышей.
Множество И’ -оптимальных стратегий во множестве S смешанных стратегий обозначим через S oaP) .
Из теоремы 2.5.2 получаем следующую теорему.
Теорема 2.7.2. Показатель эффективности L’’(P ) смешанной стратегии P = (p l ,p 2 ,...,p m) по If -критерию представляет собой взвешенное среднее показателей эффективности Ц чистых стратегий ф, i = 1,2,.,.,т, по тому же критерию с весами р, / = 1,2.....т :
Из неравенств (2.5.12) следуют неравенства ^р > аГ
Из теоремы 2.5.3 следует теорема.
Теорема 2.7.3. По критерию Лапласа относительно выигрышей цены игры в чистых и в смешанных стратегиях совпадают: Ь р с = L p s .
Па основании этой теоремы можно общее значение I!" -цеп в чистых и в смешанных стратегиях назвать просто ценой игры по критерию Лапласа относительно выигрышей и обозначить через L p .
Следствие 2.7.1 (из теоремы 2.13). Для того чтобы чистая стратегия была оптимальной во множестве смешанных стратегий по критерию Лапласа относительно выигрышей необходимо и достаточно, чтобы она была оптимальной по тому же критерию во множестве чистых стратегий.
Теоретико-множественное выражение этого следствия состоит в справедливости равенства S 1 f|S ouf) = (S c , из которого следует, что множество (^C)O(i") ст р атсги й, V" -оптимальных во множестве 5 е чистых стратегий, является подмножеством множества ) стратегий, If -оптимальных во множестве 5 смешанных стратегий: (S L) оаГ) с: S 0{lf) .
Теорема 2.5.4 дает в частности следующее утверждение.
Теорема 2.7.4. Пусть (S L)° {ir) = {ф,ф 2 ,...,ф^, 1
стратегия Р, спектр которой является подмножеством множества {,/ 2 .....i k },
будет L" -оптимальной.
Если в условиях теоремы 2.7.4 1>2 и спектр стратегии Р содержит более одного номера, то эта оптимальная смешанная стратегия не является чистой.
Геометрическая интерпретация множества S смешанных И" - оптимальных стратегий дастся в следующей теореме.
Теорема 2 . 1 . 5 . Если (S c ) 0(iP) = {Л-,Л, Ч,...,4,}. 1 йк т, то множество S 0(LP) смешанных стратегий, оптимальных по критерию Лапласа относительно выигрышей, есть симплекс размерности k- с к вершинами, изображающими оптимальные чистые стратегии А^,А и,...,А^.
Следствие 2.7.2. Если каждая чистая стратегия является оптимальной по критерию Лапласа относительно выигрышей, то и каждая смешанная стратегия также оптимальна по тому же критерию.
Следствие 2.7.3. Если среди чистых стратегий оптимальной по критерию Лапласа относительно выигрышей является только одна, то во множестве смешанных стратегий других оптимальных по этому же критерию стратегий нет.
Следствие 2.7.4. Если не все чистые стратегии являются оптимальными по критерию Лапласа относительно выигрышей, то множество S if) смешанных стратегий, оптимальных по тому же критерию, принадлежит границе Fr 5 симплекса S.
Пример 2.7.1. Рассмотрим игру с природой из примера 2.6.1, в которой т = 4, а п = 5. Из матрицы выигрышей (2.6.20) найдем по формуле (2.7.1) И" - показатели эффективности чистых стратегий:!{" = 0,2(2 + 7 + 3 + 15 + 6) = 6,6, 1!’ г =0,2 (4 +6 + 11 + 3 + 5) = 5,8, =0,2 (6+ +4 + 9 + 10 + 5) = 6,8, =0,2-(3 + 8 + 7 +
9+ 5) = 6,4. Отсюда делаем вывод, что единственной чистой If -оптимальной является стратегия А 3 .
Сравнивая полученный результат с результатом решения примера 2.6.1, видим, что по критерию Байеса относительно рисков с вектором вероятностей состояний природы «у = (0,30; 0,20; 0,15; 0,10; 0,25) и критерию Лапласа относительно вышрышей оптимальными являются разные стратегии?
Вопросы для самоконтроля знаний
- 1. В чём состоит принцип Лапласа недостаточного основания?
- 2. Покажите, что вектор вероятностей состояний природы в критерии Лапласа обладает всеми свойствами вектора вероятностей состояний природы в общем случае.
- 3. Дайте определение показателю эффективности чистой стратегии по критерию Лапласа относительно выигрышей.
- 4. Что такое цена игры в чистых стратегиях по критерию Лапласа относительно выигрышей?
- 5. Какая стратегия называется оптимальной во множестве чистых стратегий по критерию Лапласа относительно выигрышей?
- 6. Определите критерий Лапласа оптимальности смешанных стратегий относительно выигрышей.
- 7. Каковы границы изменения показателя эффективности чистой стратегии?
- 8. Каковы границы изменения цены игры?
- 9. Какова связь между показателем эффективности смешанной стратегии и показателями эффективности чистых стратегий?
- 10. Существуют ли игры с природой, в которых цена игры в чистых стратегиях отлична от цены игры в смешанных стратегиях?
- 11. Дайте геометрическую интерпретацию множеству стратегий, оптимальных во множестве смешанных стратегий по критерию Лапласа относительно выигрышей.
- 12. Что можно сказать о множестве стратегий, оптимальных во множестве смешанных стратегий по критерию Лапласа относительно выигрышей, если каждая чистая стратегия оптимальна?
- 13. Что можно сказать о множестве стратегий, оптимальных во множестве смешанных стратегий по критерию Лапласа относительно выигрышей, если среди чистых стратегий только одна является оптимальной?
- 14. Дайте определение границы множества в конечномерном евклидовом пространстве.
Задачи для самостоятельного решения
2.7.1. (Реализация химического реактива). Пусть в условиях задачи 2.1.5 состояния спроса на 11, 12 и 13 ящиков реактива ВС-6 в неделю равновероятны. По значениям выигрыш-функции (см. ответ к задаче 2.1.5) сформировать матрицу выигрышей.
Сколько ящиков реактива надо производить, чтобы среднеарифметическая прибыль была наибольшей?
Определить, при какой из смешанных стратегий Р" = (0,1; 0,5; 0,4) и Р" = (0,4; 0,5; 0,1) производства реактива ЗАО «Фото и цвет» получит большую среднеарифметическую прибыль?
- 2.7.2. (Планирование посева). Будем считать, что в условиях задачи 2.5.3 сухая, нормальная и влажная погода наступают с одинаковой вероятностью. Какую культуру посеять с тем, чтобы доход был наибольшим. Полученное решение сравнить с решением задачи 2.5.3.
- 2.7.3. Пусть игра с природой задастся платежной матрицей
Найти полное решение по выигрыш-критерию Лаиаласа. Для каждой чистой стратегии и цены игры в чистых стратегиях проиллюстрировать справедливость соответственно неравенств (2.7.4) и (2.7.5).
- 2.7.4. В условиях задачи 2.7.3 проверить на оптимальность смешанную стратегию Р° =(0,25; 0,00; 0,75). Если стратегия Р° = (0,25; 0,00; 0,75) оптимальна, то показать выполнимость для нес равенства (2.7.9). Для смешанной стратегии Р = (0,15; 0,55; 0,30) проиллюстрировать справедливость равенства (2.7.10) и неравенств (2.7.11).
- 2.7.5. (Выпуск новой продукции). Предположим, что в условиях задачи
- 2.4.5 состояния спроса равновероятны. Найти полное решение по выигрыш- критерию Лапласа и дать ему экономическую интерпретацию.
- Пьер Симон Лаплас (фр. Pierre-Simon tie Laplace) - выдающийся французский математик, физик и ас-троном, родился в Бомон-ан-Ож (Нормандия) 23 марта 1749 года в небогатой крестьянской семье. Рано проявиввыдающиеся способности, с блеском окончил в Бомон-ан-Ож школу монашеского ордена бенедиктинцев, из которой вышел, между прочим, убеждённым атеистом, и был оставлен там же в Бомоне, преподавателем математики ввоенной школе. Первую научную работу написал в 17 лет, т.е. в 1766 г., и в этом же году отправился в Париж, гдес помощью Д"Аламбера получил место преподавателя в Военной школе Парижа. Важнейшие направления научныхисследований Лапласа - математика, математическая физика, астрономия. Лаплас - один из основателей математической теории вероятностей. Получил фундаментальные результаты по интегрированию дифференциальныхуравнений в частных производных, ввел в рассмотрение производящие функции и «преобразование Лапласа», доказал биномиальный закон распределения вероятностей и первые предельные теоремы теории вероятностей. Завершил создание небесной механики. Ему принадлежат основополагающие результаты по теории устойчивостиСолнечной системы, движений Юпитера и Сатурна («законы Лапласа»), приливов и отливов, космогоническойгипотезы И. Канта («гипотеза Канта-Лапласа»), ускорения движения Луны и сжатия Земли (1787), скорости распространения звука в воздухе и плотности воздуха (1809). Лаплас - адъюнкт Французской АН (1773), профессорПарижской артиллерийской школы (1775), а затем экзаменатор Артиллерийского корпуса, председатель Палатымер и весов (1790), член Национального института (с 1795), руководитель Бюро Долгот (1795), после ВеликойФранцузской революции активно участвовал в реорганизации системы образования во Франции и в созданииВысшей нормальной и Политехнической школ. Лаплас - действительный член Парижской АП (1785), член Королевских обществ в Турине и Копенгагене (1801), член Академий наук в Гёттингене (1802), Берлине (1808), Голландии (1809), Почетный член Петербургской АП (с 1802). Во время Консулата был назначен Наполеоном министромвнутренних дел Франции, затем - вице-президентом сената (1803) и через месяц - канцлером; награжден орденом Почетного легиона (1804). В 1811 г. Наполеон присвоил ему звание графа де Лаплас, за что ученый посвятилимператору третий том своего «Трактата о небесной механике». Говорят, что на вопрос Наполеона, почему в егоТрактате нет упоминания о боге, Лаплас ответил: «Ваше величество, эта гипотеза оказалась не нужной». Послереставрации монархии Лаплас пользовался благосклонностью Людовика XVIII, который сделал его пэром Франции и пожаловал титул маркиза. В 1817 г. Лаплас стал членом вновь созданной Французской академии, т.е. - одним из сорока бессмертных. Лаплас был широко образованным человеком. По своим философским взглядам склонялся к материализму. Он знал языки, историю, философию, химию, биологию. Любил поэзию, музыку, живопись.Семейная жизнь Лапласа протекла ровно и приятно. Был женат (1778) на Шарлоте де Курти - красивой женщинес мягким, добрым характером, которая любила своего мужа, преклонялась перед ним и делала все, чтобы оградитьего от домашних забот и волнений, чтобы все свое время он мог посвящать занятиям наукой. Подарила ему дочь исына. Умер ученый 5 марта 1827 г. после недолгой болезни. Его последние слова были: «То, что мы знаем, такничтожно по сравнению с тем, что мы не знаем». (, [ 18], , ).
- критерий минимакса, критерий максимакса, критерий Байеса, критерий Вальда, критерий Сэвиджа , критерий Лапласа, критерий Ходжа-Лемана см. Типовые задания ;
- критерий Гурвица, обобщенный критерий Гурвица с расчетом эффективности.
Инструкция . Для выбора оптимальной стратегии в онлайн режиме необходимо задать размерность матрицы. Затем в новом диалоговом окне выбрать необходимые критерии и коэффициенты. Также можно вставить данные из Excel .
Примечание : Сначала, если возможно, упрощают матрицу, вычеркивая невыгодные стратегии A. Стратегии природы вычеркивать нельзя, т. к. каждое из состояний природы может наступить случайным образом, независимо от действий A .Любую хозяйственную деятельность человека можно рассматривать как игру с природой. В широком смысле под "природой" понимается совокупность неопределенных факторов; влияющих на эффективность принимаемых решений. Безразличие природы к игре (выигрышу) к возможность получения экономистом (статистиком) дополнительной информации о ее состоянии отличают игру экономиста с природой от обычной матричной игры, в которой принимают участие два сознательных игрока.
Пример . Предприятие может выпускать 3 вида продукции А 1 , А 2 и А 3 , получая при этом прибыль, зависящую от спроса, который может быть в одном из 4-х состояний (В 1 , В 2 , В 3 , В 4). Элементы платежной матрицы характеризуют прибыль, которую получат при выпуске i-й продукции при j-м состоянии спроса. Игра предприятия А против спроса В задана платежной матрицей:
|
|
В 1 |
В 2 |
В 3 |
В 4 |
|
А 1 |
2 |
7 |
8 |
6 |
|
А 2 |
2 |
8 |
7 |
3 |
|
А 3 |
4 |
3 |
4 |
2 |
Определить оптимальные пропорции в выпускаемой продукции, гарантирующие максимизацию средней величины прибыли при любом состоянии спроса, считая его определенным. Задача сводится к игровой модели, в которой.
Решение.
Критерий максимакса
.
Выбираем из (8; 8; 4) максимальный элемент max=8
Критерий Лапласа .
Выбираем из (5.75; 5; 3.25) максимальный элемент max=5.75
Вывод: выбираем стратегию N=1.
Критерий Вальда .
Выбираем из (2; 2; 2) максимальный элемент max=2
Вывод: выбираем стратегию N=1.
Критерий Севиджа
.
Находим матрицу рисков.
Риск
- мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b j = max(a ij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r 11 = 4 - 2 = 2; r 21 = 4 - 2 = 2; r 31 = 4 - 4 = 0;
2. Рассчитываем 2-й столбец матрицы рисков.
r 12 = 8 - 7 = 1; r 22 = 8 - 8 = 0; r 32 = 8 - 3 = 5;
3. Рассчитываем 3-й столбец матрицы рисков.
r 13 = 8 - 8 = 0; r 23 = 8 - 7 = 1; r 33 = 8 - 4 = 4;
4. Рассчитываем 4-й столбец матрицы рисков.
r 14 = 6 - 6 = 0; r 24 = 6 - 3 = 3; r 34 = 6 - 2 = 4;
Результаты вычислений оформим в виде таблицы.
Выбираем из (2; 3; 5) минимальный элемент min=2
Вывод: выбираем стратегию N=1.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A 1 .
Задание . Фирма планирует реализацию своей продукции на рынках, учитывая возможные варианты покупательского спроса П j , j=1,4 (низкий, средний, высокий, очень высокий). На предприятии разработано три стратегии сбыта товаров A 1 , А 2 , А 3 . Объем товарооборота (ден.ед.), зависящий от стратегии и покупательского спроса, представлен в таблице.| П 1 | П 2 | П 3 | П 4 | |
| А 1 | 30 +N | 10 | 20 | 25 + N/2 |
| А 2 | 50 | 70 - N | 10 + N/2 | 25 |
| А 3 | 25 – N/2 | 35 | 40 | 60 - N/2 |
Известны возможные состояния покупательского спроса, которые соответственно q 1 =0,3, q 2 =0,2, q 3 =0,4, q 4 =0,1. Необходимо найти стратегию сбыта, максимизирующую средний товарооборот фирмы. При этом использовать критерии Вальда, Гурвица, Сэвиджа, Байеса.
Решение
находим с помощью калькулятора .
Критерий Байеса
.
По критерию Байеса за оптимальные принимается та стратегия (чистая) A i , при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(a ij p j)
∑(a 1,j p j) = 33 0.3 + 10 0.2 + 20 0.4 + 26.5 0.1 = 22.55
∑(a 2,j p j) = 50 0.3 + 67 0.2 + 11.5 0.4 + 25 0.1 = 35.5
∑(a 3,j p j) = 23.5 0.3 + 35 0.2 + 40 0.4 + 58.5 0.1 = 35.9
| A i | П 1 | П 2 | П 3 | П 4 | ∑(a ij p j) |
| A 1 | 9.9 | 2 | 8 | 2.65 | 22.55 |
| A 2 | 15 | 13.4 | 4.6 | 2.5 | 35.5 |
| A 3 | 7.05 | 7 | 16 | 5.85 | 35.9 |
| p j | 0.3 | 0.2 | 0.4 | 0.1 |
Критерий Лапласа .
Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.:
q 1 = q 2 = ... = q n = 1/n.
q i = 1/4
| A i | П 1 | П 2 | П 3 | П 4 | ∑(a ij) |
| A 1 | 8.25 | 2.5 | 5 | 6.63 | 22.38 |
| A 2 | 12.5 | 16.75 | 2.88 | 6.25 | 38.38 |
| A 3 | 5.88 | 8.75 | 10 | 14.63 | 39.25 |
| p j | 0.25 | 0.25 | 0.25 | 0.25 |
Критерий Вальда .
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min a ij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
| A i | П 1 | П 2 | П 3 | П 4 | min(a ij) |
| A 1 | 33 | 10 | 20 | 26.5 | 10 |
| A 2 | 50 | 67 | 11.5 | 25 | 11.5 |
| A 3 | 23.5 | 35 | 40 | 58.5 | 23.5 |
Критерий Севиджа .
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max r ij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b j = max(a ij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r 11 = 50 - 33 = 17; r 21 = 50 - 50 = 0; r 31 = 50 - 23.5 = 26.5;
2. Рассчитываем 2-й столбец матрицы рисков.
r 12 = 67 - 10 = 57; r 22 = 67 - 67 = 0; r 32 = 67 - 35 = 32;
3. Рассчитываем 3-й столбец матрицы рисков.
r 13 = 40 - 20 = 20; r 23 = 40 - 11.5 = 28.5; r 33 = 40 - 40 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r 14 = 58.5 - 26.5 = 32; r 24 = 58.5 - 25 = 33.5; r 34 = 58.5 - 58.5 = 0;
| A i | П 1 | П 2 | П 3 | П 4 |
| A 1 | 17 | 57 | 20 | 32 |
| A 2 | 0 | 0 | 28.5 | 33.5 |
| A 3 | 26.5 | 32 | 0 | 0 |
| A i | П 1 | П 2 | П 3 | П 4 | max(a ij) |
| A 1 | 17 | 57 | 20 | 32 | 57 |
| A 2 | 0 | 0 | 28.5 | 33.5 | 33.5 |
| A 3 | 26.5 | 32 | 0 | 0 | 32 |
Критерий Гурвица .
Критерий Гурвица является критерием пессимизма - оптимизма. За (оптимальную принимается та стратегия, для которой выполняется соотношение:
max(s i)
где s i = y min(a ij) + (1-y)max(a ij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем s i .
s 1 = 0.5 10+(1-0.5) 33 = 21.5
s 2 = 0.5 11.5+(1-0.5) 67 = 39.25
s 3 = 0.5 23.5+(1-0.5) 58.5 = 41
| A i | П 1 | П 2 | П 3 | П 4 | min(a ij) | max(a ij) | y min(a ij) + (1-y)max(a ij) |
| A 1 | 33 | 10 | 20 | 26.5 | 10 | 33 | 21.5 |
| A 2 | 50 | 67 | 11.5 | 25 | 11.5 | 67 | 39.25 |
| A 3 | 23.5 | 35 | 40 | 58.5 | 23.5 | 58.5 | 41 |
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A 3 .
Руководство компании принимает решение о размещении производства нового продукта в некотором месте. Чтобы сформировать представление о ситуации на рынке нового продукта на момент освоения производства, ему необходимо учесть затраты на доставку готовой продукции до потребителя, развитость транспортной и социальной инфраструктуры региона, конкуренцию на рынке, соотношение спроса и предложения, курсы валют и многое другое. Возможные варианты решений, инвестиционная привлекательность которых определяется как процент прироста дохода по отношению к сумме капитальных вложений, представлены в таблице.
Выбрать:
1) место для размещения производства, если руководитель предприятия уверен в том, что на рынке сложится ситуация 4;
2) место для размещения производства, если руководство оценивает вероятность ситуации 1 в 0,2; ситуации 2 в 0,1; ситуации 3 в 0,25;
3) провести выбор варианта в условиях неопределенности по критерию: максимакс, максимин, критерий Лапласа, критерий Сэведжа, критерий Гурвица (y = 0,3);
4) изменится ли наилучший вариант решения по критерию Гурвица если величину a увеличить до 0,5?
5) предположив, что данные таблицы представляют затраты предприятия, определить выбор, который сделает предприятие при использовании каждого из следующих критериев: максимин; максимакс; критерий Гурвица(? = 0,3); критерий Сэведжа; критерий Лапласа
3. Критерий Лапласа, Вальда, Сэвиджа, Гурвица
Существует несколько критериев для выбора оптимальной стратегии при принятии решения в условиях риска и неопределенности.
Критерий Лапласа: применяется, если можно предполагать, что все варианты внешних условий одинаково вероятны. Для каждого решения находится средняя оценка по всем вариантам внешних условий (средний выигрыш):
где N– количество состояний внешней среды.

где Z – оптимальная стратегия.
Критерий Вальда: (критерий крайнего пессимизма, максиминный критерий): решение выбирается в расчете на наихудшие внешние условия. Вероятности состояний природы неизвестны и нет возможности получить о них какую-либо статистическую информацию. В качестве оценки каждого решения используется минимальный выигрыш, который можно получить при выборе этого решения:

Лучшим является решение с максимальной оценкой.

Лучшим является решение с максимальной оценкой.
По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния природы.
Критерий Сэвиджа, как и критерий Вальда, - это критерий крайнего пессимизма, но только пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше. Для оценки решений используется матрица рисков. В качестве оценки используется максимальный риск (максимальный потерянный выигрыш), соответствующий данному решению:

Лучшим является решение с минимальной оценкой.

Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски.
Критерий Гурвица: решение принимается с учетом того, что возможны как благоприятные, так и неблагоприятные внешние условия. При использовании этого критерия требуется указать «коэффициент пессимизма» – число в диапазоне от 0 до 1, представляющее собой субъективную (т.е. не рассчитанную, а указанную человеком) оценку возможности неблагоприятных внешних условий. Если есть основания предполагать, что внешние условия будут неблагоприятными, то коэффициент пессимизма назначается близким к единице. Если неблагоприятные внешние условия маловероятны, то используется коэффициент пессимизма, близкий к нулю. Оценки решений находятся по следующей формуле:
где a – коэффициент пессимизма.
Лучшим является решение с максимальной оценкой:

Кроме критериев оптимальности, которые можно применять при принятии решения в условиях риска и неопределенности, существует очень известный и распространенный метод теории игр, используемый в управленческой деятельности в условиях неопределенности.
4. Метод теории игр при принятии решений в условиях неопределенности
При принятии решений в условиях неопределенности очень широко используется метод теории игр. Теория игр – это математическая теория конфликтных ситуаций. Задача этой теоpии – выработка рекомендаций по рациональному образу действий участников конфликта. При этом строят упрошенную модель конфликтной ситуации, называемую игрой. Под «игрой» понимают мероприятие, состоящее из ряда действий или «ходов». От реальной конфликтной ситуации игра отличается тем, что ведется по вполне определенным правилам. Стороны, участвующие в конфликте, называют игроками, исход конфликта - выигрышем и т.д.
Если в игре сталкиваются интересы двух сторон, то игра называется парной, если сторон больше - множественной. Множественная игра с двумя постоянными коалициями обращает игру в парную. Наибольшее практическое значение имеют парные игры. Рассматрим конечную игру, в которой игрок А имеет m стратегий, а игрок В - n стратегий. Такая игра называется m x n. Стратегии, соответственно, обозначим: А 1 , А 2 , ..., А m - для игрока А; В 1 , В 2 , ..., В n - для игрока В. Если игра состоит только из личных ходов, то выбор стратегий А i и В j игроками однозначно определяет исход игры - наш выигрыш a ij Если известны a ij для всех сочетаний стратегий, то они образуют платежную матрицу размером m x п, где: m - число строк матрицы, а n - число его столбцов.
Принцип осторожности, диктующий игрокам выбор соответствующих стратегий (максиминной и минимаксной), является в теории игр основным принципом и называется принципом минимакса. В платежной матрице такой игры существует элемент, являющийся одновременно минимальным в своей строке и максимальным в своем столбце. Такой элемент называют седловой тонкой. При этом значение v=ą=þ называют чистой ценой игры. В этом случае решение игры (совокупность оптимальных стратегий игроков) обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии . Если верхняя цена игры не совпадает с нижней, то в этом случае стоит говорить об игре в смешанных стратегиях. Смешанной S A называется применение чистых стратегий А 1 ,А 2 ,…,А n с вероятностью p 1 ,p 2 ,…,p n , а смешанной стратегией S B - применение чистых стратегий B 1 ,B 2 ,…,B n с вероятностью p 1 ,p 2 ,…,p m . Пусть игра имеет размерность 2 на 2 и задается платежной матрицей:

Для игрока А оптимальная стратегия будет иметь вероятности:
 ;
;
 ;
цена игры
;
цена игры
Этот критерий опирается на известный принцип недостаточного обоснования. Поскольку вероятности состояний q 1 , q 2 , ... ,q n не известны, необходимая информация для вывода, что эти вероятности различны, отсутствует. В противном случае можно было бы определить эти вероятности и ситуацию уже не следовало рассматривать как принятие решения в условиях неопределенности. Так как принцип недостаточного обоснования утверждает противоположное, то состояния q 1 , q 2 , ... ,q n имеют равные вероятности. Если согласиться с приведенными доводами, то исходную задачу можно рассматривать как задачу принятия решений в условиях риска, когда выбирается действие a i , дающее ожидаемый выигрыш.
Другими словами, находится действие a i * , соответствующее
Вероятность реализации состояния q j (j =1,2, ... ,n),
Пример. Одно из предприятий должно определить уровень предложения услуг так, чтобы удовлетворить потребности клиентов в течение предстоящих праздников. Точное число клиентов не известно, но ожидается, что оно может принять одно из четырех значений: 200, 250, 300 или 350 клиентов. Для каждого из этих возможных значений существует наилучший уровень предложения (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения предложения над спросом, либо из-за неполного удовлетворения спроса.
Является наиболее осторожным, поскольку основывается на выборе наилучшей из наихудших возможностей. Если результат n (a i , q j) представляет потери лица, принимающего решение, для действия a i наибольшие потери независимо от возможного состояния q j будут равны

В этом случае критерий называется максиминным.
Подходы к учету неопределенности при описании рисков. В теории принятия решений в настоящее время при компьютерном и математическом моделировании для описания неопределенностей чаще всего используют такие математические средства, как: вероятностно-статистические методы, методы статистики нечисловых данных, в том числе интервальной статистики и интервальной математики, а также методы теории нечеткости, - методы теории конфликтов (теории игр). Они применяются в имитационных, эконометрических, экономико-математических моделях, реализованных обычно в виде программных продуктов. Некоторые виды неопределенностей связаны с безразличными к организации силами - природными (погодные условия) или общественными (смена правительства). Если явление достаточно часто повторяется, то его естественно описывать в вероятностных терминах. Так, прогноз урожайности зерновых вполне естественно вести в вероятностных терминах. Если событие единично, то вероятностное описание вызывает внутренний протест, поскольку частотная интерпретация вероятности невозможна. Так, для описания неопределенности, связанной с исходами выборов или со сменой правительства, лучше использовать методы теории нечеткости, в частности, интервальной математики (интервал – удобный частный случай описания нечеткого множества). Наконец, если неопределенность связана с активными действиями соперников или партнеров, целесообразно применять методы анализа конфликтных ситуаций, т.е. методы теории игр, прежде всего антагонистических игр, но иногда полезны и более новые методы кооперативных игр, нацеленных на получение устойчивого компромисса. Иногда под уменьшением риска понимают уменьшение дисперсии случайной величины, поскольку при этом уменьшается неопределенность. В теории принятия решений риск - это плата за принятие решения, отличного от оптимального, он обычно выражается как математическое ожидание. В экономике плата измеряется обычно в денежных единицах, т.е. в виде финансового потока (потока платежей и поступлений) в условиях неопределенности.
13.Критерий Сэвиджа
Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или проигрышей) v(а i , s j) матрицей потерь r(а i , s j), которая определяется следующим образом.

По принципу Сэвиджа каждое решение характеризуется величиной дополнительных потерь, которые возникают при реализации этого решения, по сравнению с реализацией решения, правильного при данном состоянии природы. Естественно, что правильное решение не влечет за собой никаких дополнительных потерь, и их величина равна нулю.
При выборе решения, наилучшим образом соответствующего различным состояниям природы, следует принимать во внимание только эти дополнительные потери, которые по существу, будут являться следствием ошибок выбора.
Для решения задачи строится так называемая “матрица рисков”, элементы которой показывают, какой убыток понесет игрок (ЛПР) в результате выбора неоптимального варианта решения.