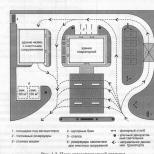
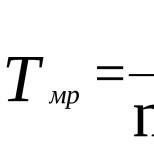Система массового обслуживания с отказами кратко. Одноканальная смо с отказами. Одноканальные СМО с ожиданием

Для СМО с отказами :

Для СМО с неограниченным ожиданием как абсолютная, так и относительная пропускная способности теряют смысл, так как каждая поступившая заявка рано или поздно будет обслужена. Для такой СМО важными показателями являются:

Для СМО смешанного типа используются обе группы показателей: как относительная и абсолютная пропускная способности , так и характеристики ожидания.

В зависимости от цели операции массового обслуживания любой из приведенных показателей (или совокупность показателей) может быть выбран в качестве критерия эффективности.

Аналитической моделью СМО является совокупность уравнений или формул, позволяющих определять вероятности состояний системы в процессе ее функционирования и рассчитывать показатели эффективности по известным характеристикам входящего потока и каналов обслуживания.

Всеобщей аналитической модели для произвольной СМО не существует . Аналитические модели разработаны для ограниченного числа частных случаев СМО. Аналитические модели, более или менее точно отображающие реальные системы, как правило, сложны и труднообозримы.

Аналитическое моделирование СМО существенно облегчается, если процессы, протекающие в СМО, марковские (потоки заявок простейшие, времена обслуживания распределены экспоненциально). В этом случае все процессы в СМО можно описать обыкновенными дифференциальными уравнениями, а в предельном случае, для стационарных состояний - линейными алгебраическими уравнениями и, решив их, определить выбранные показатели эффективности.

Рассмотрим примеры некоторых СМО.

2.5.1. Многоканальная СМО с отказами

Пример 2.5 . Три автоинспектора проверяют путевые листы у водителей грузовых автомобилей. Если хотя бы один инспектор свободен, проезжающий грузовик останавливают. Если все инспекторы заняты, грузовик, не задерживаясь, проезжает мимо. Поток грузовиков простейший, время проверки случайное с экспоненциальным распределением.

Такую ситуацию можно моделировать трехканальной СМО с отказами (без очереди). Система разомкнутая, с однородными заявками, однофазная, с абсолютно надежными каналами.

Описание состояний:

Все инспекторы свободны;

Занят один инспектор;

Заняты два инспектора;

Заняты три инспектора.

Граф состояний системы приведен на рис. 2.11 .

На графе: - интенсивность потока грузовых автомобилей; - интенсивность проверок документов одним автоинспектором.

Моделирование проводится с целью определения части автомобилей, которые не будут проверены.

Решение

Искомая часть вероятности - вероятности занятости всех трех инспекторов. Поскольку граф состояний представляет типовую схему "гибели и размножения", то найдем , используя зависимости (2.2).

Пропускную способность этого поста автоинспекторов можно характеризовать относительной пропускной способностью :

Пример 2.6 . Для приема и обработки донесений от разведгруппы в разведотделе объединения назначена группа в составе трех офицеров. Ожидаемая интенсивность потока донесений - 15 донесений в час. Среднее время обработки одного донесения одним офицером - . Каждый офицер может принимать донесения от любой разведгруппы. Освободившийся офицер обрабатывает последнее из поступивших донесений. Поступающие донесения должны обрабатываться с вероятностью не менее 95 %.

Определить, достаточно ли назначенной группы из трех офицеров для выполнения поставленной задачи.

Решение

Группа офицеров работает как СМО с отказами, состоящая из трех каналов.

Поток донесений с интенсивностью можно считать простейшим, так как он суммарный от нескольких разведгрупп. Интенсивность обслуживания . Закон распределения неизвестен, но это несущественно, так как показано, что для систем с отказами он может быть произвольным.

Описание состояний и граф состояний СМО будут аналогичны приведенным в примере 2.5.

Поскольку граф состояний - это схема "гибели и размножения", то для нее имеются готовые выражения для предельных вероятностей состояния:

Отношение называют приведенной интенсивностью потока заявок . Физический смысл ее следующий: величина представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

В примере .

В рассматриваемой СМО отказ наступает при занятости всех трех каналов, то есть . Тогда:

Так как вероятность отказа в обработке донесений составляет более 34 % (), то необходимо увеличить личный состав группы. Увеличим состав группы в два раза, то есть СМО будет иметь теперь шесть каналов, и рассчитаем :

Таким образом, только группа из шести офицеров сможет обрабатывать поступающие донесения с вероятностью 95 %.

2.5.2. Многоканальная СМО с ожиданием

Пример 2.7 . На участке форсирования реки имеются 15 однотипных переправочных средств. Поток поступления техники на переправу в среднем составляет 1 ед./мин, среднее время переправы одной единицы техники - 10 мин (с учетом возвращения назад переправочного средства).

Оценить основные характеристики переправы, в том числе вероятность в немедленной переправе сразу по прибытии единицы техники.

Решение

Абсолютная пропускная способность , т. е. все, что подходит к переправе, тут же практически переправляется.

Среднее число работающих переправочных средств:

Коэффициенты использования и простоя переправы:

Для решения примера была также разработана программа. Интервалы времени поступления техники на переправу, время переправы приняты распределенными по экспоненциальному закону.

Коэффициенты использования переправы после 50 прогонов практически совпадают: .

Рассмотрим -канальную СМО с отказами. Будем нумеровать состояния системы по числу занятых каналов (или, что в данном случае то же, по числу заявок, связанных с системой). Состояния будут:

Все каналы свободны,

Занят ровно один канал, остальные свободны,

Заняты ровно k каналов, остальные свободны,

Заняты все каналов.

Граф состояний СМО представлен на рис. 5.3. Разметим граф, т. е. проставим у стрелок интенсивности соответствующих потоков событий.

По стрелкам слева направо систему переводит один и тот же поток - ноток заявок с интенсивностью к. Если система находится в состоянии (занято k каналов) и пришла новая заявка, система переходит (перескакивает) в состояние

Определим интенсивности потоков событий, переводящих систему по стрелкам справа налево.

Пусть система находится в состоянии 5, (занят один канал). Тогда, как только закончится обслуживание заявки, занимающей этот канал, система перейдет в значит, поток событий, переводящий систему по стрелке имеет интенсивность Очевидно, если обслуживанием занято два канала, а не один, поток обслуживание переводящий систему но стрелке будет вдвое интенсивнее если занято k каналов в k раз интенсивнее Проставим соответствующие интенсивности у стрелок, ведущих справа налево.

Из рис. 5.3 видно, что процесс, протекающий в СМО, представляет собой частный случай процесса гибели и размножения, рассмотренного нами в § 8 гл. 4.

Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:

Уравнения (4.1) называются уравнениями Эрланга. Естественными начальными условиями для их решения являются:

(в начальный момент система свободна).

Интегрирование системы уравнений (4.1) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно, на АВМ или ЭЦВМ. Такое решение дает нам все вероятности состояний

как функции времени.

Естественно, нас больше всего будут интересовать предел -ные вероятности состояний характеризующие установившийся режим работы СМО (при ). Для нахождения предельных вероятностей воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения в § 8 гл. 4. Согласно этому решению,

В этих формулах интенсивность потока заявок и интенсивность потока обслуживаний (для одного канала) не фигурируют по отдельности, а входят только своим отношением Обозначим это отношение

и будем называть величину р «приведенной интенсивностью» потока заявок. Физический смысл ее таков: величина представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом этого обозначения, формулы (4.2) примут вид:

Формулы (4.3) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров ( - интенсивность потока чаявок, - интенсивность обслуживания, п - число каналов СМО).

Зная все вероятности состояний

можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А и вероятность отказа .

Действительно, заявка получает отказ, если приходит в момент, когда все каналов заняты. Вероятность этого равна

Вероятность того, что заявка будет принята к обслуживанию (она же относительная пропускная способность q) дополняет Яотк до единицы:

Абсолютная пропускная способность:

Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число

Величину k можно вычислить непосредственно через вероятности по формуле:

как математическое ожидание дискретной случайной величины, принимающей значения с вероятностями Однако значительно проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которую мы уже знаем. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени-, один занятый канал обслуживает в среднем за единицу времени заявок; среднее число занятых каналов получится делением А на

Классификация СМО и их основные характеристики

Системы массового обслуживания делятся на типы (или классы) по ряду признаков. Первое деление: СМО с отказами и СМО с очередью . В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует. Примеры СМО с отказами встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты, получает отказ и покидает СМО необслуженной. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной. На практике чаще встречаются (и имеют большее значение) СМО с очередью; недаром теория массового обслуживания имеет второе название: «теория очередей».

СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь-ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»). При анализе СМО должна учитываться также и «дисциплина обслуживания» - заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречается так называемое обслуживание с приоритетом - некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютным - когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания заявку с низшим (например, пришедший в парикмахерскую клиент высокого ранга прогоняет с кресла обыкновенного клиента), так и относительным - когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.

Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, затем получить на контроле).

Кроме этих признаков, СМО делятся на два класса: «открытые» и «замкнутые». В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО - зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки. Это - пример замкнутой СMO.

В зависимости от типа СМО при оценке её эффективности могут применяться те или иные величины (показатели эффективности). Например, для СМО с отказами одной из важнейших характеристик её продуктивности является так называемая абсолютная пропускная способность – среднее число заявок, которое может обслужить система за единицу времени. Наряду с абсолютной, часто рассматривается относительная пропускная способность – средняя доля поступивших заявок, обслуживаемая системой (отношение среднего числа обслуживаемых в единицу времени заявок к среднему числу поступающих заявок за это время). Помимо этого при анализе СМО с отказами могут интересовать ещё среднее число занятых каналов, среднее относительное время простоя системы в целом и отдельного канала и т.д.

Характеристики СМО с ожиданиями. Для СМО с неограниченным ожиданием абсолютные и относительные пропускные способности теряют смысл. Зато важными являются: среднее число заявок в очереди, среднее число заявок в системе (в очереди и под обслуживанием), среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе и другие. Для СМО с ограниченным ожиданием интерес представляют обе группы характеристик.

Для анализа процесса, протекающего в СМО, существенно знать основные параметры системы: число каналов n , интенсивность потока заявок l, производительность каждого канала (среднее число заявок , обслуживаемых непрерывно занятым каналом в единицу времени), условия образования очереди (ограничения, если они есть).

Условимся все потоки событий, переводящие СМО из состояния в состояние, считать пуассоновскими.

Простейшая задача. Пусть СМО состоит только из одного канала (n=1 ) и на нее поступает пуассоновский поток заявок с интенсивностью l, зависящей в общем случае от времени l=l(t) (9.1). Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени Т об, распределенного по показательному закону с параметром m f(t)= me - m t (t>0) (9.2).

Из этого следует, что «поток обслуживаний» - простейший, с интенсивностью m. Требуется найти: абсолютную (А) и относительную (q ) пропускные способности.

Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний: S 0 – свободен, S 1 – занят. Обозначим вероятности состояний p 0 (t) и p 1 (t) . Очевидно:

"t p 0 (t)+p 1 (t)=1 (9.3).

Граф состояний системы

По графу состояний системы составим дифференциальные уравнения Колмогорова:

(9.4)

В соответствии с (9.3) одно уравнение в (9.4) лишнее. Отбросим второе уравнение, а первое перепишем с учетом (9.3):

или (9.5).

Это уравнение естественно решать при начальных условиях p 0 (0)=1; p 1 (0)=0. Уравнение (9.5) легко может быть решено не только для простейшего потока заявок (l=const), но и для случая l=l(t). Приведем решение (9.5) только для случая l=const: .

Для нашего случая вероятность p 0 есть не что иное, как q .

Действительно, p 0 есть вероятность того, что в момент t канал свободен, иначе вероятность того, что заявка, пришедшая в момент t , будет обслужена. А значит, для данного момента времени t среднее число обслуженных заявок к числу поступивших также равно p 0: q= p 0 .

В пределе, при t®¥, когда процесс обслуживания уже установится, предельное значение q будет равно .

Легко найти и А, зная q . Они связаны очевидным соотношением:. В пределе, при t®¥, А тоже установится и будет равна .

Зная q (вероятность того, что пришедшая в момент t заявка будет обслужена) легко найти вероятность отказа: P отк =1-q. P отк есть не что иное, как средняя доля необслуженных заявок среди поданных. В пределе, при t®¥ .

Система Эрланга
В качестве показателей эффективности СМО с отказами будем рассматривать:
А - абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени;
Q - относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;
P отк. - вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;
- среднее число занятых каналов (для многоканальной системы).
Одноканальная система с отказами . Рассмотрим задачу.
Имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ 1 . Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет два состояния: S 0 - канал свободен, S 1 - канал занят. Размеченный граф состояний представлен на рис. 6.

Рис. 6
В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид.
(18)
т.е. система вырождается в одно уравнение. Учитывая нормировочное условие p 0 +p 1 =1, найдем из (18) предельные вероятности состояний
(19)
которые выражают среднее относительное время пребывания системы в состоянии S 0 (когда канал свободен) и S 1 (когда канал занят), т.е. определяют соответственно относительную пропускную способность Q системы и вероятность отказа P отк:
(20)
(21)
Абсолютную пропускную способность найдем, умножив относительную пропускную способность Q на интенсивность потока отказов
(22)
Задача 5. Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью λ, равной 90 заявок в час, а средняя продолжительность разговора по телефону об. =2 мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.
Решение. Имеем λ=90 (1/ч), об. =2 мин. Интенсивность потока обслуживании μ=1/ об =1/2=0,5 (1/мин)=30 (1/ч). По (20) относительная пропускная способность СМО (Q=30/(90+30)=0,25, т.е. в среднем только 25% поступающих заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит Р отк. =0,75 (см. (21)). Абсолютная пропускная способность СМО по (29) ,A=90∙0,25=22,5, т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.
Многоканальная система с отказами . Рассмотрим классическую задачу Эрланга.
Имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S 0 , S 1 , S 2 , …, S k , …, S n , где S k - состояние системы, когда в ней находится k заявок, т.е. занято k каналов.
Граф состояний СМОсоответствует процессу гибели и размножения и показан на рис. 7.

Рис. 7
Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью λ. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии S 2 (два канала заняты), то она может перейти в состояние. S 1 (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет 2μ. Аналогично суммарный поток обслуживаний, переводящий СМО из состояния S 3 (три канала заняты) в S 2 . будет иметь интенсивность Зμ, т.е. может освободиться любой из трех каналов и т.д.
В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния
(23)
где членыразложения будут представлять собой коэффициенты приp 0 в выражениях для предельных вероятностей p 1 , p 2 , …, p k , …, p n . Величина
(24)
называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала. Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь
(25) есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем μ заявок (в единицу времени), то среднее число занятых каналов
(30)
или, учитывая (29), (24):
(31)

Рассмотрим многоканальную систему массового обслуживания (всего каналов n), в которую поступают заявки с интенсивностью λ и обслуживаются с интенсивностью μ. Заявка, прибывшая в систему, обслуживается, если хотя бы один канал свободен. Если все каналы заняты, то очередная заявка, поступившая в систему, получает отказ и покидает СМО. Пронумеруем состояния системы по числу занятых каналов:

• S 0 – все каналы свободны;
• S 1 – занят один канал;
• S 2 – занято два канала;
• S k – занято k каналов;
• S n – все каналы заняты.

Рис. 7.24
На рисунке 6.24 изображен граф состояний, в котором S i – номер канала; λ – интенсивность поступления заявок; μ – соответственно интенсивность обслуживания заявок. Заявки поступают в систему массового обслуживания с постоянной интенсивностью и постепенно занимают один за другим каналы; когда все каналы будут заняты, то очередная заявка, прибывшая в СМО, получит отказ и покинет систему.
Определим интенсивности потоков событий, которые переводят систему из состояния в состояние при движении как слева направо, так и справа налево по графу состояний.
Например, пусть система находится в состоянии S 1 , т. е. один канал занят, поскольку на его входе стоит заявка. Как только обслуживание заявки закончится, система перейдет в состояние S 0 .
Например, если заняты два канала, то поток обслуживания, переводящий систему из состояния S 2 в состояние S 1 будет вдвое интенсивнее: 2-μ; соответственно, если занято k каналов, интенсивность равна k-μ.

Процесс обслуживания является процессом гибели и размножения. Уравнения Колмогорова для этого частного случая будут иметь следующий вид:

(7.25)
Уравнения (7.25) называются уравнениями Эрланга .
Для того, чтобы найти значения вероятностей состояний Р 0 , Р 1 , …, Р n , необходимо определить начальные условия:
– Р 0 (0) = 1, т. е. на входе системы стоит заявка;
– Р 1 (0) = Р 2 (0) = … = Р n (0) = 0, т. е. в начальный момент времени система свободна.
Проинтегрировав систему дифференциальных уравнений (7.25), получим значения вероятностей состояний Р 0 (t ), Р 1 (t ), … Р n (t ).
Но гораздо больше нас интересуют предельные вероятности состояний. При t → ∞ и по формуле, полученной при рассмотрении процесса гибели и размножения, получим решение системы уравнений (7.25):

(7.26)
В этих формулах отношение интенсивности λ / μ к потоку заявок удобно обозначить ρ .Эту величину называют приведенной интенсивностью потока заявок, то есть среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом сделанных обозначений система уравнений (7.26) примет следующий вид:

(7.27)
Эти формулы для вычисления предельных вероятностей называются формулами Эрланга .
Зная все вероятности состояний СМО, найдем характеристики эффективности СМО, т. е. абсолютную пропускную способность А , относительную пропускную способность Q и вероятность отказа Р отк.
Заявка, поступившая в систему, получит отказ, если она застанет все каналы занятыми:

.
Вероятность того, что заявка будет принята к обслуживанию:

Q = 1 – Р отк,
где Q – средняя доля поступивших заявок, обслуживаемых системой, или среднее число заявок обслуженных СМО в единицу времени, отнесенное к среднему числу поступивших за это время заявок:

A=λ·Q=λ·(1-P отк)
Кроме того, одной из важнейших характеристик СМО с отказами является среднее число занятых каналов . В n -канальной СМО с отказами это число совпадает со средним числом заявок, находящихся в СМО.
Среднее число заявок k можно вычислить непосредственно через вероятности состояний Р 0 , Р 1 , … , Р n:

,
т. е. находим математическое ожидание дискретной случайной величины, которая принимает значение от 0 до n с вероятностями Р 0 , Р 1 , …, Р n .
Еще проще выразить величину k через абсолютную пропускную способность СМО, т.е. А. Величина А – среднее число заявок, которые обслуживаются системой в единицу времени. Один занятый канал обслуживает за единицу времени μ заявок, тогда среднее число занятых каналов