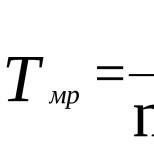Пять способов сделать ожидание в очереди менее утомительным. Многоканальная смо без ограничения на длину очереди, но с ограничением на время ожидания

В этом разделе рассмотрим СМО типа М/М/n/m< , но, в отличие от предыдущих, наложим ограничение на время ожидания в очереди.
Это ограничение носит принципиальный характер, т.к. при вычислении вероятностей состояний СМО необходимо знание не только текущего состояния (числа требований в системе), но и того, как давно пришли требования, ожидающие обслуживания. Таким образом, процесс К(t) перестает быть марковским.

Время ожидания в очереди может быть ограничено как детерминированной, так и случайной величиной. В обеих случаях процесс К(t), как уже было сказано, характеризуется наличием последействия. Однако, способы формирования на его основе марковской модели СМО существенно различаются.

7.3.1. Время ожидания ограничено случайной величиной τ

В этом случае все зависит от закона распределения ограничения , т.к. именно ограничение вносит в систему последействие. Поэтому вернуть процессу К(t) марковость крайне просто. Достаточно принять для описания случайной величины экспоненциальное распределение. Однако при этом нельзя забывать, что такая операция возможна лишь в том случае, когда реальное распределение или действительно экспоненциальное, или близко к нему. Если это не так, то сформированная математическая модель будет неадекватна реальной СМО.

При экспоненциально распределенном ограничении на время ожидания в очереди, процесс изменения числа требований в СМО по-прежнему будет процессом размножения и гибели с той лишь разницей, что интенсивность гибели увеличится за счет, покидающих очередь требований, у которых время ожидания превысило допустимую величину.

Примем, что распределение времени ожидания имеет вид:

F(t) = 1 - e - функция распределения,

f(t) = e - плотность распределения,

где - интенсивность выхода из очереди за счет превышения допустимого времени ожидания.

Тогда параметры процесса К(t) будут равны:

K , при к

N + (k - n) , при к>n .

Читателю предлагается самостоятельно, руководствуясь материалом раздела 7.2.1, написать модель рассматриваемой СМО, и формулы для вычисления основных характеристик СМО в стационарном режиме.

7.3.2. Время ожидания ограничено неслучайной величиной τ

В этом случае для описания СМО с помощью марковской модели целесообразно использовать второй из приведенных в 7.1. способов, а именно, расширение понятия состояния. Для того, чтобы прогнозировать распределения состояний в будущем, необходимо знать как давно пришли в систему требования, которые в настоящее время находятся в очереди. Это можно сделать, включив в число обобщенных координат, описывающих состояние СМО, давность прихода каждого ожидающего требования, или, что то же самое, время, которое осталось у него до окончания срока ожидания. В рамках процесса К(t), которым мы пользовались во всех предыдущих задачах, это сделать нельзя, и в рассматриваемом случае модель функционирования СМО строится на основании векторного случайного процесса X , характеризующего состояние системы через состояния каждого из n ее каналов:

X = { X (t), X (t),…. X (t)} = { X (t)}

X (t) – это время, которое осталось до освобождения j-ого канала. Таким образом, для каждого момента времени t, мы можем прогнозировать будущие состояния каналов: j-ый канал освободится через х j (t), если за это время не поступят требования из внешнего потока. А так как входящий поток простейший, это значит, что в процессе X последействие отсутствует, т.е. процесс марковский. Найдем распределение этого процесса.

(7.3)

Это функция и плотность n-мерного распределения вектора X (t) в случае, когда все каналы заняты. Занятые (и только они) каналы персонифицированы, т.е. перенумерованы.

То же, что и выше, но в случае, когда занято лишь «к» каналов, а остальные свободны.

(7.4)

В дальнейшем, для простоты, будем трактовать плотность f (t; x …x ) как вероятность того, в СМО занято к каналов, которым присвоены номера от 1 до к., опуская при этом формальное умножение на . Знание этих распределений позволит вычислять вероятности состояний рассматриваемой системы.

Для вывода необходимых уравнений используем марковское свойство процесса X(t), а именно: будем выражать вероятность состояния процесса в момент t+ t (будущее) через его состояние в момент t (настоящее). Предварительно заметим, что - вероятность того, что в системе нет требований.

Для нулевого состояния СМО (в системе нет требований) можем, как и прежде, записать

(7.5)

Второе слагаемое означает, что в момент t в одном из каналов системы было требование, обслуживание которого заканчивалось на интервале t , и этим каналом мог быть любой из n.

Преобразуя и переходя к пределу при t 0, получим:

(7.6)

Рассмотрим случай, когда 0

(7.6)

При составлении этого уравнения учитывалось следующее:

· за время t занятости всех каналов уменьшаются на , и если за это время не подойдет ни одного требования входящего потока, то к моменту t система окажется в нужном состоянии (первое слагаемое правой части);

· второе слагаемое правой части: в момент t был занят к-1 канал, а канал с номером i (из числа персонифицированных) был пустым, и что бы СМО пришла в нужное состояние необходимо: чтобы пришло требование, чтобы время его обслуживания было равно x , и чтобы из (n-к) свободных каналов оно выбрало именно i-ый, причем этим каналом может быть любой из каналов с номерами от 1 до к.

· последнее слагаемое означает, что в момент t был занят (к + 1) канал, но в одном из них (а именно в (к+1)–ом) на интервале обслуживание заканчивалось. Причем таким каналом может быть любой из (n – к).

Теперь рассмотрим случай, когда :

(7.7)

Поясним, как и выше, содержание правой части:

· Первое слагаемое отличается от случая кsign x =1, если x>0, и sign x= - 1, если x<0 ).

· Второе слагаемое в содержательном плане ничем не отличается от случая к

· Третье слагаемое правой части отвечает ситуации, когда все каналы заняты, как это нужно, но один из них «недозанят», например, X (t) = Z < x ; для того, чтобы в момент t+ СМО оказалась в требуемом состоянии надо, чтобы на интервале пришло требование со временем обслуживания (x - z), и стало бы в очередь к i-му каналу, а для этого его занятость z должна быть меньше занятости любого другого канала (z < min x ) т.к. когда все каналы заняты, требование автоматически становится в очередь к тому который раньше освободится; при этом недозанятым может быть любой из n каналов.

Вспоминая определение смешанной частной производной:

,(7.8)

производя группировку членов уравнений, как это делалось выше, и переходя к пределу при , окончательно получим:

(7.9)

(7.10)

Эти уравнения относятся к стационарному режиму, что получило свое выражение в том, что производные плотностей распределения по t приняты равными нулю, а сами плотности записаны в финальной форме, как функции не зависящие от времени. Кроме того, для простоты последующих выкладок, приняты следующие обозначения: f = f и f = f .

Решение этой системы, т.е. отыскание функций f и f , произведем следующим образом. Вначале, исходя из общих соображений содержательного характера, найдем вид этих функций, после чего подставим их в систему уравнений с целью установить, удовлетворяют они им или нет. Если ответ будет положительным, то решение системы уравнений найдено.

Сперва рассмотрим случай 0 . Как говорилось выше, функция f имеет смысл вероятности того, что в СМО занято «к» персонофицированных (перенумерованных) каналов, причем первый освободится через x единиц времени, второй через x , … , к-ый через x . Каналы функционируют независимо, и время обслуживания в каждом распределено экспоненциально. Тогда вероятность рассматриваемого события равна:

(7.11)

Вероятность того, что занято k перенумерованных каналов

P - вероятность того, что в СМО занято k каналов

1. Одноканальная СМО с ожиданием и ограничением на длину очереди. На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов; кассир, выдающий зарплату). В теории массового обслуживания одноканальные СМО с очередью также занимают особое место: именно к таким СМО относится большинство полученных до сих пор аналитических формул для немарковских систем.

Рассмотрим одноканальную СМО, на вход которой поступает простейший поток заявок с интенсивностью λ . Предположим, что поток обслуживаний также простейший с интенсивностью μ . Это означает, что непрерывно занятый канал обслуживает в среднем μ заявок в единицу времени. Заявка, поступившая в СМО в момент, когда канал занят, в отличие от СМО с отказами, не покидает систему, а становится в очередь и ожидает обслуживания.

Далее предполагаем, что в данной системе имеется ограничение на длину очереди, под которой понимается максимальное число мест в очереди, а именно, предполагаем, что в очереди могут находиться максимум m ≥1 заявок. Поэтому заявка, пришедшая на вход СМО, в момент, когда в очереди уже стоят m заявок, получает отказ и покидает систему необслуженной.

Таким образом, рассматриваемая СМО относится к системам смешанного типа с ограничением на длину очереди.

Пронумеруем состояния СМО по числу заявок, находящихся в системе, т.е. под обслуживанием и в очереди:

S 0 – канал свободен (следовательно, очереди нет);

S 1 – канал занят и очереди нет, т.е. в СМО находится (под обслуживанием) одна заявка;

S 2 – канал занят и в очереди стоит одна заявка;

……………………………………………………..

S m +1 – канал занят и в очереди m заявок.

Граф состояний данной СМО представлен на рис. 6 и совпадает с графом, описывающим процесс гибели и размножения, с тем отличием, что при наличии только одного канала обслуживания все интенсивности потоков обслуживаний равны μ .

Рис. 6. Схема состояний в одноканальной системе с очередью

Для описания предельного режима работы СМО можно воспользоваться изложенными правилами и формулами. Запишем сразу выражения, определяющие предельные вероятности состояний:

где ρ = λ/μ – интенсивность нагрузки канала.

Если λ = μ , то получаем .

Пусть теперь
. Выражение дляp 0 можно в данном случае записать проще, пользуясь тем, что в знаменателе стоит сумма m + 2 членов геометрической прогрессии со знаменателем ρ :

.

Заметим, что при m = 0 мы переходим к уже рассмотренной одноканальной СМО с отказами. В этом случае .

Определим основные характеристики одноканальной СМО с ожиданием: относительную и абсолютную пропускные способности, вероятность отказа, а также среднюю длину очереди и среднее время ожидания заявки в очереди.

Поступившая на вход СМО заявка получает отказ тогда и только тогда, когда канал занят и в очереди ожидают m заявок, т.е. когда система находится в состоянии S m +1 . Поэтому вероятность отказа определяется вероятностью появления состояния S m +1 :

Относительная пропускная способность, или доля обслуживаемых заявок, поступающих в единицу времени, определяется выражением:

Заметим, что относительная пропускная способность Q совпадает со средней долей принятых (т.е. не получивших отказ) в систему заявок среди всех поступивших, поскольку заявка, попавшая в очередь, непременно будет обслужена.

Абсолютная пропускная способность системы

.

Среднее число заявок L оч , стоящих в очереди на обслуживание, определяется как математическое ожидание дискретной случайной величины k – числа заявок, стоящих в очереди:

.

Случайная величина k принимает значения 0, 1, 2, … , m , вероятности которых определяются вероятностями состояний системы p k . Таким образом, закон распределения дискретной случайной величины k имеет следующий вид:

Поэтому по определению математического ожидания дискретной случайной величины (с учетом формул для вероятностей состояний) получаем:

(16)

Предположим, что ρ ≠ 1 . Очевидно, имеем:

Но сумма представляет собой сумму первых m членов геометрической прогрессии

. (17)

Подставив выражение (17) в (16), найдем:

или, используя равенство
(полученное приρ ≠ 1 ), имеем

Если же ρ = 1 , то из равенства (16)
а учитывая, что в этом случае
и
(суммаm членов арифметической прогрессии), окончательно получаем

.

Тогда среднее число заявок в очереди

(18)

Важной характеристикой СМО с ожиданием является среднее время ожидания заявки в очереди
. Пусть T оч – непрерывная случайная величина, представляющая собой время ожидания заявки в очереди. Среднее время ожидания заявки в очереди вычислим как математическое ожидание этой случайной величины:

.

Для вычисления математического ожидания воспользуемся формулой полного математического ожидания: если об условиях опыта можно сделать n (попарно) несовместных гипотез
то полное математическое ожидание случайной величиныX может быть вычислено по формуле

где M (X | H k ) – условное математическое ожидание величины X при гипотезе H k .

Рассмотрим m + 2 несовместных гипотез H k , k = 0,1,..., m + 1 , состоящих в том, что СМО находится соответственно в состояниях S k , k = 0,1,..., m + 1 . Вероятности этих гипотез p (H k ) = p k , k = 0,1,..., m +1 .

Если заявка поступает в СМО при гипотезе H 0 S 0 , в котором канал свободен, то заявке не придется стоять в очереди и, следовательно, условное математическое ожидание M (
| H 0 ) случайной величины
при гипотезе H 0 ,совпадающее со средним временем ожидания заявки в очереди при гипотезе H 0 , равно нулю.

Для заявки, поступившей в СМО при гипотезе H 1 , т.е. когда СМО находится в состоянии S 1 , в котором канал занят, но очереди нет, условное математическое ожидание M (
| H 1 ) случайной величины
при гипотезе H 1 , совпадающее со средним временем ожидания заявки в очереди при гипотезе H 1 , будет равно среднему времени обслуживания одной заявки
.

Условное математическое ожидание M (
| H 2 ) случайной величины
при гипотезе H 2 , т.е. при условии, что заявка поступила в СМО, находящуюся в состоянии S 2 , в котором канал занят и в очереди уже ждет одна заявка, равно 2/ μ (удвоенному среднему времени обслуживания, поскольку нужно обслужить две заявки: ту, которая находится в канале обслуживания, и ту, которая ждет в очереди). И так далее.

Если заявка поступит в систему при гипотезе H m , т.е. когда канал занят и в очереди ждут m − 1 заявок, то M (
| H m ).

Наконец, заявка, пришедшая в СМО при гипотезе H m +1 , т.е. когда канал занят, m заявок стоят в очереди, и свободных мест в очереди больше нет, получает отказ и покидает систему. Поэтому в этом случае M (
| H m +1 ) = 0.

Следовательно, по формуле полного математического ожидания среднее время ожидания заявки в очереди

Подставляя сюда выражения для вероятностей p k (k =1,2,...,m ), получаем:
(19)

Если интенсивность нагрузки канала ρ ≠ 1 , то из равенства (19) с учетом формул (17), (18), а также выражения для p 0 находим:

Если же ρ = 1 , то, подставляя в равенство (19) выражение p 0 = 1/(m +2), значение суммы
, используя формулу (18) приρ = 1 и учитывая, что в данном случае μ = λ , будем иметь

Итак, для любого ρ получаем формулу для среднего времени пребывания заявки в очереди, которая называется формулой Литтла:
т.е. среднее время ожидания заявки в очереди
равно среднему числу заявок в очереди L оч , деленному на интенсивность λ входящего потока заявок.

Пример. На автозаправочной станции (АЗС) имеется одна колонка. Площадка при станции, на которой машины ожидают заправку, может вместить не более трех машин одновременно, если она занята, то очередная машина, прибывшая к станции, в очередь не становится, а проезжает на соседнюю АЗС. В среднем машины прибывают на станцию каждые 2 мин. Процесс заправки одной машины продолжается в среднем 2,5 мин. Определить основные характеристики системы.

Решение. Математической моделью данной АЗС является одноканальная СМО с ожиданием и ограничением на длину очереди (m = 3). Предполагается, что поток машин, подъезжающих к АЗС для заправки, и поток обслуживаний – простейшие.

Поскольку машины прибывают в среднем через каждые 2 мин, то интенсивность входящего потока равна λ =1/2 = 0,5 (машин в минуту). Среднее время обслуживания одной машины
= 2,5 мин, следовательно, интенсивность потока обслуживаний μ =1/2,5 = 0,4 (машины в минуту).

Определяем интенсивность нагрузки канала: ρ = λ/μ = 0,5/0,4 = 1,25.

Вычисляем вероятность отказа
откуда относительная пропускная способность и абсолютная пропускная способность A = λ Q ≈ 0,5⋅0,703 ≈ 0,352.

Среднее число машин, ожидающих в очереди на заправку

Среднее время ожидания машины в очереди находим по формуле Литтла
= L оч /λ ≈1,559/0,5 = 3,118.

Таким образом, из анализа работы СМО следует, что из каждых 100 подъезжающих машин 30 получают отказ (P отк ≈ 29,7%), т.е. обслуживаются 2/3 заявок. Поэтому необходимо либо сократить время обслуживания одной машины (увеличить интенсивность потока обслуживаний), либо увеличить число колонок, либо увеличить площадку для ожидания.

1. Интенсивность нагрузки .
ρ = λ t обс = 120 1/60 = 2
Интенсивность нагрузки ρ=2 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
3. Вероятность, что канал свободен (доля времени простоя каналов).

Следовательно, 12% в течение часа канал будет не занят, время простоя равно t пр = 7.1 мин.
Вероятность того, что обслуживанием:
занят 1 канал:
p 1 = ρ 1 /1! p 0 = 2 1 /1! 0.12 = 0.24
заняты 2 канала:
p 2 = ρ 2 /2! p 0 = 2 2 /2! 0.12 = 0.24
заняты 3 канала:
p 3 = ρ 3 /3! p 0 = 2 3 /3! 0.12 = 0.16
4. Доля заявок, получивших отказ .

Значит, 3% из числа поступивших заявок не принимаются к обслуживанию.
5. Вероятность обслуживания поступающих заявок .
В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому:
p отк + p обс = 1
Относительная пропускная способность: Q = p обс.
p обс = 1 - p отк = 1 - 0.0311 = 0.97
Следовательно, 97% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.
6. Среднее число каналов, занятых обслуживанием .
n з = ρ p обс = 2 0.97 = 1.9 каналов
Среднее число простаивающих каналов .
n пр = n - n з = 3 - 1.9 = 1.1 каналов
7. Коэффициент занятости каналов обслуживанием .

Следовательно, система на 60% занята обслуживанием.
8. Абсолютная пропускная способность .
A = p обс λ = 0.97 120 = 116.3 заявок/час.
.
t пр = p отк t обс = 0.0311 0.0166 = 0 час.
10. Среднее число заявок, находящихся в очереди .

ед.
(среднее время ожидания обслуживания заявки в очереди).
час.
12. Среднее число обслуживаемых заявок .
L обс = ρ Q = 2 0.97 = 1.94 ед.
13. Среднее число заявок в системе .
L CMO = L оч + L обс = 0.51 + 1.94 = 2.45 ед.
13. Среднее время пребывания заявки в СМО .
час.
Число заявок, получивших отказ в течение часа: λ p 1 = 4 заявок в час.
Номинальная производительность СМО: 3 / 0.0166 = 181 заявок в час.
Фактическая производительность СМО: 116.3 / 181 = 64% от номинальной производительности.

Рассмотрим СМО с п каналами. На вход системы поступает простейший поток заявок с плотностью l . Время ожидания заявки в очереди Т ож распределено по показательному закону со средним значением . Время обслуживания показательное со средним значением . Параметр n полностью аналогичен параметрам l и m . Его можно интерпретировать, как плотность «потока уходов» заявки, стоящей в очереди.

Пусть максимальное число мест в очереди ограничено и равно т .

В этом случае система имеет т + n + 1 состояние. Размеченный граф состояний выглядит так:

Можно составить уравнения, аналогичные уравнениям Эрланга для предельного стационарного режима при t ® ¥ вероятности состояний, полученные из этих уравнений запишутся так:

, (6.1)

, (6.2)

где .

Параметры a и b выражают соответственно среднее число заявок и среднее число уходов заявки, стоящей в очереди, приходящиеся на среднее время обслуживания одной заявки. Данные формулы достаточно громоздки и требуют большой вычислительной работы. Поэтому их можно записать в другом виде:

(6.3)

(6.4)

Если d не является целым, то вычисление можно провести для двух ближайших к величине d целых числе и произвести между ними линейную интерполяцию.

Средне число занятых каналов определяем по формуле:

(6.5)

Вероятность обслуживания заявки Р обс = .

Если число мест в очереди не ограничено (т ® ¥), то формулы упрощаются с учетом того, то .

Если заявки, попавшие в очередь, не покидают ее, а терпеливо дожидаются обслуживания (n = 0, а значит, и b = 0), то формулы (6.1) и (6.2) превращаются в формулы (5.1), (5.2), которые мы рассматривали в § 5).

Если при этом длина очереди не ограничена (т ® ¥), то получим формулы (4.1), (4.2), мак как система превращается в чистую систему с ожиданием (см. § 4).

Задача 1 . В магазине обслуживают покупателей четыре продавца. Среднее время обслуживания одного покупателя 4 мин. Плотность потока покупателей около двух человек в минуту. В очереди могут ожидать одновременно не более 20 человек. В среднем покупатель, вставший в очередь, ожидает 10 мин., после чего он покидает магазин.

Определить: 1) среднее число занятых продавцов;

2) среднее число покупателей, ожидающих в очереди;

3) вероятность того, что все места в очереди будут заняты;

4) вероятность того, что покупатель будет обслужен;

5) среднее время пребывания в очереди;

6) среднее время, затачиваемое на всю процедуру (ожидание в очереди и обслуживание).

Решение . Работа магазина может быть представлена как работа СМО смешанного типа. Параметры этой системы следующие:

п = 4 – число каналов обслуживания;

т = 20 – максимальное число мест в очереди;

– среднее число покупателей, приходящих в магазин;

– среднее время обслуживания одного покупателя ;

– среднее время ожидания покупателя в очереди. После чего он покидает магазин ;

; ; – целое число.

1) Среднее число занятых продавцов:

то есть практически все продавцы будут заняты.

2) Среднее число покупателей, ожидающих в очереди:

3) Вероятность того, что все места в очереди будут заняты:

то есть все места в очереди будут заняты с вероятностью менее 1 %.

4) Вероятность обслуживания:

6) Среднее время, затачиваемое на всю процедуру:

Задача 2 . С целью увеличения дальности беспосадочного полета производится дозаправка самолетов горючим в воздухе. В районе дозаправки постоянно дежурят четыре самолета-дозаправщика. Если дозаправка началась, то она осуществляется до конца и длится в среднем 10 минут. Если все дозаправщики заняты, то самолет, нуждающийся в дозаправке, может некоторое время «ожидать» (совершать полет по кругу в районе дозаправки); среднее время ожидании 20 минут. Если самолет не дождался дозаправки в воздухе, он садится на запасной аэродром. Интенсивность полетов такова, что в среднем за час в район дозаправки прибывает 24 самолета. Число самолетов, ожидающих дозаправки в воздухе, не ограничено.

Определить: 1) вероятность Р об с того, что самолет будет дозаправлен;

2) среднее число занятых дозаправщиков;

3) вероятность того, что произвольно взятый дозаправщик будет занят;

4) среднее время простоя дозаправщика.

Решение . Рассматриваемая система может быть рассмотрена как СМО смешанного типа с параметрами:

число каналов обслуживания п = 4;

число мест в очереди не ограничено (т ® ¥);

плотность потока заявок ;

плотность потока обслуживаний ;

плотность потока уходов из очереди .

Отсюда – целое число.

По формуле (6.5) находим среднее число дозаправщиков, занятых обслуживанием самолетов:

где R (¥;8) = 1.

Вероятность тог, что самолет будет дозаправлен:

Среднее время простоя дозаправщика:

Задачи .

1. Гарантийная мастерская принимает заказы на ремонт по одному телефону. Среднее число заказов за 1 час – 2п . Среднее время оформления заявки т мин. Считается, что если клиент позвонил, а телефон занят, то он обратится в другую мастерскую (система без очереди). Найти основные характеристики СМО: 1) р 0 , р 1 ; 2) р обс ; 3) ; 4) . Проанализировать, как изменятся соответствующие показатели, если подключить второй телефон. С какой интенсивностью должны работать два работника, чтобы доля потерь заявок была менее 10 %? , менее 5 %?

2. В мастерской по ремонту холодильников имеются 3 мастера. Мастер в среднем может отремонтировать 1 холодильник за 80 минут. Рабочий день составляет 8 часов. В мастерскую в среднем поступает 40 заявок на ремонт за рабочий день. В случае, если все мастера заняты, холодильник в ремонт не принимается (СМО с отказом). Заработная плата мастеров почасовая,

150 рублей в час. Клиент в среднем платит за ремонт 300 рублей (запчасти оплачиваются отдельно). Определить чистую прибыль мастерской за смену. Как изменится прибыль, если пригласить в мастерскую 4-го мастера? Определить количество мастеров, при котором прибыль мастерской максимальна.

3. В платной справочной телефонной службе имеется четыре телефонные линии. В справочную поступает простейший поток заявок со средней интенсивностью 1 заявка в 2 минуты. Ответ на каждый вопрос длится в среднем 6 минут. За ответ на каждый вопрос клиент платит 10 руб.. Эксплуатация одного канала обслуживания составляет 30 руб./час, создание канала обслуживания требует расхода 8000 руб. Определить чистый доход за один час. Через сколько часов произойдет окупаемость системы?

4. Гарантийная мастерская принимает заказы на ремонт по одному телефону. Среднее число поступающих в течение часа заказов – 20, среднее время оформления заказа – 4 минуты. Определить показатели СМО:

1) вероятности состояний системы р 0 , р 1 ; 2) вероятность обслуживания заявки р обс ; 3) среднее число занятых каналов ; 4) вероятность занятости канала; 5) среднее время простоя канала. Проанализировать, как они изменятся, если подключить второй телефон.

5. Средний интервал между поступающими в прокатный пункт заявками и запросами на наличие определенных предметов составляет 5 мин. Принимают заявки два работника, каждый с интенсивностью 12 заявок в час. С какой интенсивностью должен работать один работник, выполняя работу двух, чтобы доля потерянных требований осталась на прежнем уровне? На сколько требуется повысить интенсивность обслуживания двум работникам, чтобы доля потерянных заявок была менее 10 %?

6. На диспетчерском пункте дежурят 4 приемщика заявок на ремонт телерадиоаппаратуры. Заявки принимаются по телефону. В диспетчерский пункт поступает простейший поток заявок с плотностью l = 3 (заявки в минуту). Вызов, поступивший в момент, когда все приемщики заняты, получает отказ. Средняя длительность оформления заявки 2 минуты. Найти все характеристики СМО: 1) вероятности состояний системы р 0 , р 1 ;

2) вероятность обслуживания заявки р обс ; 3)среднее число занятых каналов ; 4) вероятность занятости канала; 5) среднее время простоя канала.

С какой интенсивностью должны работать 2 работника, выполняя работу четырех, чтобы доля потерянных требований осталась на прежнем уровне?

7. Библиотека принимает заявки на книги по одному телефону. Среднее число поступающих в течение часа заявок – 70, среднее время оформления заявки – 2 минуты. Определить показатели СМО (задача 6). Найти, как изменятся параметры системы, если заявки будут приниматься по двум телефонам и при этом доля потерянных заявок уменьшится в 2 раза по сравнению с прежним уровнем. Как изменится время пребывания заявки в системе?

8. Пусть в СМО с отказом поступает в среднем 15 заявок в час. Среднее время обслуживания заявки составляет 12 мин. За обслуживание заявки клиент платит 80 рублей. Содержание одного канала обслуживания обходится 100 рублей в час. Определить число каналов обслуживания, при которых прибыль максимальна.

Литература

1. Венцель Е.С. Теория вероятностей. М., 1962.

2. Венцель Е.С., Овчаров Л.А. Теория вероятностей. М., 1969.

3. Гнеденко Б.В. Лекции по теории массового обслуживания. Изд. КВИРТУ, 1960.

4. Н.Ш.Кремер Теория вероятностей и математическая статистика. Учебник. 2-е издание. Москва, 2003, 2006 ЮНИТИ.

Изучим работу n-канальной (n > 1) СМО с ожиданием, на вход которой поступает простейший поток заявок П вх с интенсивностью. Поток обслуживании каждым каналом также предполагается простейшим с интенсивностью µ. На длину очереди никаких ограничений не налагается, но время ожидания каждой заявки в очереди ограничено случайным сроком Т ож со средним значением, после которого заявка покидает систему необслуженной. Временной интервал Т ож является непрерывной случайной величиной, которая может принимать любое положительное значение и математическое ожидание которой.

Если этот поток пуассоновский, то процесс, протекающий в СМО, будет Марковским.

Такие системы часто встречаются на практике. Их иногда называют системами с «нетерпеливыми» заявками.

Занумеруем состояния СМО по числу заявок, находящихся в системе, как под обслуживанием, так и стоящих в очереди: S k (k = 0,1,…n) - k заявок под обслуживанием (k каналов заняты, очереди нет), S n+r (r = 1,2,…) - п заявок под обслуживанием (все п каналов заняты) и r заявок в очереди.

Таким образом, СМО может пребывать в одном из бесконечного множества состояний.

Размеченный граф состояний указан на рис. 1.

Рис. 1.

Из состояния в состояние слева направо СМО переходит под воздействием одного и того же входящего потока заявок П вх с интенсивностью. Следовательно, плотности вероятностей этих переходов

k-1,k = , k = 1,2,… (1)

Переход СМО из состояния без очереди S k , k = 1,…,n , в соседнее слева состояние S k-1 , (k = 1,…,n) (в котором также не будет очереди) происходит под действием суммарного потока, слагающегося из к потоков обслуживания занятых каналов, интенсивность которого, представляющая собой сумму интенсивностей слагаемых потоков обслуживании, равна kµ . Поэтому под стрелками налево от состояния s n до состояния s 0 проставлены плотности вероятностей переходов

k,k-1 =kµ, k = 1,…,n (2)

На систему в состоянии с очередью S n+r , r = 1,2,… , действует суммарный поток - результат наложения n потоков обслуживании и r потоков уходов. Поэтому интенсивность суммарного потока равна сумме интенсивностей слагаемых потоков nµ+rщ . Этот суммарный поток порождает переход СМО справа налево из состояния S n+r ,(r = 1,2,…) в среднее S n+r-1 ,(r = 1,2,…) и, таким образом,

k,k-1 =nµ+(k-n)щ, k =n+1,n+2,… (3)

Итак, плотности вероятностей переходов системы справа налево, учитывая (2) и (3), можно записать в объединённой форме

Структура графа говорит о том, что процесс, протекающий в СМО, является процессом гибели и размножения.

Подставим (1) и (4) для k=1,…,n+m в формулу

Введем в рассмотрение величину, которую можно назвать приведенной интенсивностью потока уходов, и которая показывает среднее число уходов из очереди не обслуженных заявок за среднее время обслуживания одной заявки. Подставляя в (5) и получим:

Так как в рассматриваемой СМО нет ограничений на длину очереди, то заявка, поступившая во входящем потоке, будет принят; в систему, т.е. отказ со стороны системы заявка не получает. Поэтому для СМО с «нетерпеливыми» заявками вероятность принятия в систему p сист =1, а вероятность отказа принятия в систему p отк =0 . Понятие «отказа принятия в систему» не следует смешивать с понятием «отказа в обслуживании», поскольку, в силу «нетерпеливости», не каждая поступившая (принятая) в систему заявка, будет обслужена. Таким образом, имеет смысл говорить о вероятности ухода заявки из очереди p ху и вероятности того, что заявка будет обслужена, p об . При этом, вероятность p об представляет собой относительную пропускную способность Q и p ху =1- p об .

Подсчитаем среднее число заявок в очереди. Для этого рассмотрим дискретную случайную величину N оч представляющую собой число заявок в очереди. Случайная величина N оч может принять любое целое неотрицательное значение, а ее закон распределения имеет вид

где p= p 0 + p 1 +…+ p n . Следовательно,

или подставляя сюда (7), получим

На каждую заявку в очереди действует поток «уходов» Пух с интенсивностью щ. На среднюю очередь, состоящую из заявок, будет действовать суммарный поток, складывающийся из потоков «уходов», и имеющий интенсивность. Значит, из среднего числа заявок в очереди в среднем будет уходить, не дождавшись обслуживания, заявок в единицу времени, а оставшиеся заявки будут обслужены. Следовательно, среднее число заявок, обслуженных за единицу времени, т.е. абсолютная пропускная способность СМО

Тогда по определению относительной пропускной способности,

Q = A/ = (-)/ = 1 - (щ/),

где щ/ = показывает среднее число уходов из очереди не обслуженных заявок за среднее время между поступлениями двух соседних заявок во входящем потоке П вх .

Среднее число занятых каналов (среднее число заявок, находящихся под обслуживанием) можно получить как отношение абсолютной пропускной способности А к производительности одного канала µ. Воспользовавшись равенством (11), будем иметь:

Среднее число занятых каналов можно подсчитать и независимо от среднего числа заявок в очереди, а именно как математическое ожидание дискретной случайной величины К, представляющей собой число занятых каналов, закон распределения которой имеет вид

где p = p n + p n+1 +…+ p n+1 + …. Но так как событие, состоящее в том, что все n каналов заняты, противоположно событию, состоящему в том, что не все n каналов заняты, а вероятность последнего события равна

p 0 + p 1 + p 2 +…+ p n-1 , то p = 1 - (p 0 + p 1 + p 2 +…+ p n-1) .

Но тогда из (11) получим:

Используя формулы (11) и (13), получим формулу для среднего числа заявок, находящихся в системе:

Выведем формулу для среднего времени ожидания заявки в очереди. Оно будет зависеть от данного среднего времени ограничивающего продолжительность пребывания заявки в очереди, для которого либо

либо найдется натуральное число i > 2 такое, что

Умножая неравенства (14) и (15) на, получим соответственно неравенства

Рассмотрим случай (14) и несовместные гипотезы состоящие в том, что система находится в состоянии. Вероятности этих гипотез

Если заявка поступит в СМО при гипотезет.е. когда система пребывает в одном из состояний в каждом из которых не все каналы заняты, то заявке не придется ожидать в очереди -она сейчас же попадет под обслуживание свободного канала. Поэтому условное математическое ожиданиеслучайной величинывремени ожидания заявки в очереди при гипотезе, представляющее собой среднее время ожидания заявки в очереди при гипотезеравно нулю:

Если заявка поступит в систему при гипотезет.е. когда СМО находится в одном из состоянийв котором все п к-п заявок (при к = п в очереди заявок нет), то среднее время освобождения одного из п занятых каналов равно, а среднее время обслуживания к-п заявок, стоящих в очереди перед поступившей в систему заявкой, равно Поэтому среднее время, необходимое для того, чтобы подошла очередь на обслуживание поступившей заявки, равно.Так как, то в силу правого неравенства (14),

Таким образом, среднее время, необходимое для того, чтобы поступившая в систему заявка была принята к обслуживанию, больше времени, ограничивающего пребывание заявки в очереди. Поэтому поступившая заявка задержится в очереди на среднее времяи покинет систему не обслуженной. Следовательно, условное математическое ожидание величиныпри гипотезе

Теперь рассмотрим те же гипотезыв случае (15). В этом случае также справедливы равенства (16).

Если заявка поступит в систему при одной из гипотез т.е., когда СМО находится в одном из состояний в котором все п каналов заняты и в очереди перед поступившей заявкой уже стоят к-п заявок (при к - n в очереди заявок нет), то так же, как и в случае (14), среднее время, необходимое для того, чтобы подошла очередь этой заявки на обслуживание, равно ограничивающим пребывание заявки. Так както, в силу левого неравенства (15),

Таким образом, среднее время, необходимое для того, чтобы пришедшая в систему заявка была принята к обслуживанию, не больше среднего времени, ограничивающего пребывание заявки в очереди. Поэтому поступившая заявка не уйдет из очереди и дождется приема на обслуживание, потратив на ожидание в очереди среднее время Следовательно, условное математическое ожидание случайной величины Т оч при гипотезе

Пусть теперь заявка поступила в систему при одной из гипотез Н ю к = n+i- т.е., когда СМО находилась в одном из состояний..., в котором все п каналов заняты и в очереди уже стоят к-п заявок. Так как то из неравенства (15):

а потому пришедшая заявка задержится в очереди на среднее время Следовательно, условное математическое ожидание случайной величины Т оч при гипотезе

По формуле полного математического ожидания получим:

В случае (15) поступившая заявка будет принята к обслуживанию, если только в момент её поступления СМО находится в одном из состояний тогда вероятность того, что заявка будет обслужена

При / = 1 формула (25) превращается в (24), поэтому для вероятности обслуживания можно записать одну формулу:

Зная вероятность обслуживания, можно вычислить вероятность ухода заявки из очереди не обслуженной:

Среднее время пребывания заявки в системе можно вычислить по формуле

где- среднее время обслуживания одной заявки, относящееся ко всем заявкам, как обслуженным, так и ушедшим из очереди, которое можно подсчитать па формуле

6. Построение и анализ модели систем массового обслуживания

Рассмотрим практическую задачу на использование СМО без ограничения на длину очереди, но с ограничением на время ожидания в очереди.

С целью увеличения дальности беспосадочного полета производится дозаправка самолетов горючим в воздухе. В районе дозаправки постоянно дежурят два самолета-дозаправщика. Дозаправка одного самолета длится в среднем около 10 минут. Если оба самолета-дозаправщика заняты, то самолет, нуждающийся в дозаправке, некоторое время может «ожидать» (совершать полет по кругу в районе дозаправки). Среднее время ожидания - 20 минут. Самолет, не дождавшийся дозаправки, вынужден садиться на запасной аэропорт. Интенсивность полетов такова, что в среднем за 1 час в район дозаправки прибывает 12 самолетов. Определить:

Вероятность того, что самолет будет дозаправлен.

Среднее число занятых дозаправщиков.

Среднее число самолетов в очереди.

Среднее число самолетов под обслуживанием.

Необходимо вычислить основные характеристики эффективности данной СМО, при условии, что заданы следующие входные параметры:

• · количество каналов обслуживания;
• · интенсивность входящего потока заявок;
• · интенсивность потока обслуживания;
• · среднее время, ограничивающее пребывание заявок в очереди.

Рассматриваемая СМО является многоканальной системой массового обслуживания без ограничения на длину очереди, но с ограничением на время ожидания. Количество каналов, интенсивность входящего потока заявок, интенсивность потока обслуживания и количество мест в очереди заданы.

В данной СМО каждый канал обслуживает в каждый момент времени одну заявку. Если в момент поступления новой заявки свободен хотя бы один канал, то пришедшая заявка поступает на обслуживание, если же заявки отсутствуют, то система простаивает.

Определим, что происходит, когда к моменту поступления заявки все каналы заняты - она становится в очередь и ожидает освобождения одного из каналов. Если в момент поступления заявки все места в очереди заняты, то эта заявка покидает систему.

Критерии эффективности функционирования СМО:

• · Вероятность простоя системы;
• · Вероятность отказа системы;
• · Относительная пропускная способность.
• · Среднее время пребывания заявки в очереди.

Данная система моделируется многоканальной СМО с «нетерпеливыми» заявками.

Параметры системы:

число каналов обслуживания n = 2 ;

интенсивность входящего поток заявок = 12 (самолетов в час);

интенсивность потока обслуживания µ = 6 (самолетов в час);

среднее время, ограничивающее пребывание заявки в очереди, следовательно, интенсивность потока уходов щ = 1/= 3 (самолета) в час.

Расчеты произведены с помощью разработанной в Turbo Pascal программе. Язык Turbo-Pascal - один из самых распространенных языков программирования компьютеров. К важным достоинствам языка Turbo-Pascal относится небольшой размер компилятора, высокая скорость трансляции программ, компиляции и их компоновки. Кроме того, удобство и высокое качество дизайна диалоговой оболочки, делают написание и отладку программ наиболее удобным в сравнении с альтернативными языками нового поколения.

Для анализа работы СМО необходимо исследовать поведение данной системы при различных входных параметрах.

В первом варианте л=12, µ=6, щ=3, число каналов n=2.

Во втором варианте л=12, µ=6, щ=3, число каналов n=3.

В третьем варианте л=12, µ=6, щ=4, число каналов n=2.

Все результаты расчетов приведены в Приложение 2.

В результате анализа полученных данных (Приложение 2), были сделаны следующие выводы.

С увеличением числа каналов увеличивается вероятность простоя системы и вероятность дозаправки на 50%.

При изменение же только времени пребывания заявки в очереди, не увеличивая кол-во каналов, изменилась интенсивность потока уходов, в результате уменьшилось число обслуживаемых самолетов и число самолетов в очереди.

По-моему мнению, необходимо набрать и обучить дополнительный обслуживающий персонал, чтобы увеличить интенсивность потока уходов, тогда будет меньше затрачиваться времени на простой дозаправщиков и не возникнет необходимости в дополнительном канале.

Хотя, выбирая наиболее оптимальные параметры, при которых работа СМО будет наиболее эффективной, нужно еще учитывать технический и экономический фактор, так как приобретение дополнительного канала обслуживания или изменение интенсивности потока уходов, требует определенных материальных затрат и затрат на подготовку кадров.