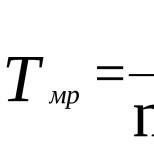Подготовка опорного плана. Вырожденность опорного плана транспортной задачи. Как избавиться
ГМ состоит из двух этапов.
2) Среди всех решений необходимо найти такое решение при котором Z достигает своего либо max или min.
Grad показывает наискорейшее возрастание функции. (С – коэффициент) (линии уровня)
1. задача имеет единственное решение.
2. Задача имеет – бесконечно много решений.
3. Задача не имеет решений а) нет ОДР б) в случаи когда zmax - ф-ия не ограниченной сверху линией уровня и наоборот.
Графический метод можно применять если имеется только две переменные или задача может быть приведена с помощью эквивалентных преобразований к задаче с двумя переменными.
Свойства допустимых планов.
1) Выпуклая линейная комбинация точек. х1 х2 …хk сумма вида α1х1+ α2х2+ ...+ αkxk , где αi =1 (αi>=0 αi – коэффициент линейной комбинации).
2) Выпуклым множеством называется такое множество т. Д на плоскости, когда вместе с любыми двумя точками Х1є Д; Х2 є Д принадлежащим множеству Д. Ему принадлежит и их выпуклая Л.К. х=tx1+(1-t)x2 є Д 0<=t<=1
3) Крайняя точка – т.Х выпуклого множества называется крайней если она не может быть представлена в виде выпуклой Л.К. любых двух точек этого множества (n=2)
Опорное решение – это допустимое базисное решение имеющая не более чем m положительных элементов, и причем векторы столбца матрицы соответственно положительны координатам вектора линейны независимы.
Свойства допустимых планов.
Теорема №1
Множество допустимых планов З.Л.П. выпукла если оно не пусто.
Дано: Д- не является пустым множеством – ОДР
Доказать Ж Д- выпуклое множество.
Х1 єД; Х2 єД,то оно удовлетворяет системе ограничений в З.Л.П. Z=cx->max Ax=b X>=0
Ax1=b 0<=t<=1
Ax2=b (1-t) => tAx1+(1-t)Ax2=bt+b(1-t) = A=b
x1; x2>=0 => x>=0
Ax=b X- решение задачи.
Х = tx1+(1-t)x2 0<=t<=1, согласно опр. Имеем выпуклое множество – Д, т.к. с любыми двумя точками ему принадлежит и их выпуклая Л.К.
Теорема № 2
Если целевая функция имеет максимум на выпуклом многограннике решений, то это максимум достигается в вершине многогранника..
Дано: Zmax->X 0 Док-ть X 0- вершина.
Док-во: Дан многогранник. А,В,С,Д,Е – вершины. (Док-во проведем от противного)
X 0 – не вершина, тогда согласно опр. Крайней точки, X 0 – не крайняя точка, и может быть представлена в виде выпуклой Л.К. точек хi є ОДР
C X 0 >Cxi (т.к. С X 0 ->max)
X 0 = αiXi αi=1 αi>=0
Найдем значение функции Z=C X 0 =CαiXi=αiCXi<αiCX 0 =CX 0 αi=CX 0
В каждом слагаемом сменим Xi на Х 0
СХ 0 Теорема №3 Об альтернативном оптимуме. Если целвевая функция достигает своего оптимального значения в нескольких вершинах (т)
х1 х2 хk , то она достигает оптимального значения в их выпуклой линейной комбинации.
Дано: Док-ть: х= αiXi Xi , i:=1,k αi=1 αi>=0 CX=d Найдем Z=СХ=CαiXi=αiCXi=αid=dαi=d Теорема № 4 Вектор Х является опорным решением тогда и только тогда, если он является вершиной многогранника. Если переменных n>3 то говорят гиперплоскость, положение точек в т – мерном пространстве.
ИДЕЯ СИМПЛЕКС МЕТОДА. Симплекс метод является универсальным. Симплекс метод – аналитический метод. 1. Находятся первоначальное, опорное решение. А)система ограничений должна быть записана в виде равенств (каноническая форма) Б)Преобразовать что бы bi >=0 i=1,m С)Привести систему к единичному базисному виду с неотрицательной правой частью. Поэтому за разрешающий элемент выбирается строго положительный элемент. Д)Приравниваем свободные к 0 , получаем первоначальное базисное неотрицательное решение, которое является опорным решением данной задачи и соответствует вершине. 2. Рассматривая функцию цели выясняем является ли полученное решение оптимальным. 3. Если полученное решение не является оптимальным, то необходимо перейти к следующей вершине (опорному решению) Переход осуществляется по определенному правилу по которому: только одна изи базисных переменных должна перейти в свободную и только одна из свободных перейти в базисную. Алгебра симплекс метода. Подсчитаем количество ограничений-равенств в нашей транспортной задаче. На первый взгляд их пять. Однако если сложить первые два, то получится такое же равенство, как и при сложении последних трех ограничений: В таких случаях математики говорят, что записанные пять ограничений не являются независимыми. Поскольку первые два ограничения в сумме означают то же самое, что и последние три, фактически ограничений, влияющих на значения переменных решения, не пять, а четыре. Поскольку ограничения в этой задаче образуют систему уравнений относительно переменных решения, можно было бы попытаться решить эту систему, чтобы найти значения переменных. Но переменных решения в нашей задаче 6, а независимых уравнений для их решения только 4. Можно произвольно положить значение двух каких -нибудь переменных решения равными 0 (например, Хп=0 и Х]2=0), тогда остальные переменные решения могут быть однозначно определены из системы уравнений, образованной ограничениями. Получившийся план перевозок, разумеется, необязательно будет оптимальным, но он обязательно является допустимым, поскольку удовлетворяет всем ограничениям. Такой план называется опорным. От множества других допустимых планов он отличается тем, что число ненулевых переменных решения (ненулевых перевозок) точно равно количеству независимых ограничений в транспортной задаче или, иначе, сумме числа поставщиков и потребителей минус 1. В нашей задаче число ненулевых перевозок в опорном плане равно 2 (количество поставщиков) + 3 (количество потребителей) -1=4. В общем случае если имеется т поставщиков и п потребителей, то количество ненулевых перевозок в опорном плане будет т + п - 1. Если, например, т = 10, а п = 20, то количество переменных будет 200, а количество ненулевых переменных в опорном плане - только 29. В теории линейного программирования доказывается, что оптимальный план обязательно является опорным. Иными словами, искать оптимальный план перевозок нужно только среди опорных планов. В этом и состоит основное значение опорного плана. Разумеется, опорных планов может быть много. В нашем примере нетрудно пересчитать, что существует 15 различных способов присвоить нули двум переменным из шести (т.е. имеется 15 опорных планов). В случае когда т = 10, п = 20, число различных опорных планов будет выражаться огромным числом 7,18*1034. Таким образом, о том, чтобы перебрать все возможные опорные планы и выбрать среди них оптимальный, в общем случае транспортной задачи, разумеется, не может быть и речи. Однако возможность осуществлять поиск только среди опорных планов все равносильно упрощает задачу по сравнению с общей задачей линейного программирования. Опорным называется такой план, в котором количество ненулевых перевозок равно сумме количеств поставщиков и потребителей минус единица. Оптимальный план перевозок следует искать только среди множества опорных планов. Наибольшее распространение для нахождения начальных опорных планов получили: Метод северо- западного угла и Метод минимального элемента. Метод северо-западного угла
используют для нахождения произвольного опорного плана ТЗ. Основную идею метода рассмотрим на конкретном примере. Пример 1. Условия ТЗ заданы транспортной таблицей (табл. 3.1). Таблица 3.1 Требуется найти опорное решение (построить опорный план). Решение.
Будем заполнять таблицу 3.1 перевозками постепенно, начиная с левой верхней ячейки(1.1) (северо-западного угла).Будем рассуждать при этом следующим образом. Пункт В 1 подал заявку на 18 единиц товара. Удовлетворим эту заявку за счет запаса 48, имеющегося в пункте А 1 , и запишем перевозку 18 в клетке (1.1). После этого заявка пункта В 1 удовлетворена, а в пункте А 1 осталось еще 30 единиц товара. Удовлетворим за счет них заявку пункта В 2 (27 единиц), запишем 27 единиц в клетке (1,2); оставшиеся 3 единицы пункта А 1 назначим пункту В 3 . В составе заявке пункта В 3 остались неудовлетворенными 39 единиц. Из них 30 покроем за счет пункта А 2 , чем его запас будет исчерпан, и еще 9 возьмем из пункта А 3 . Из оставшихся 18 единиц пункта А 3 12 выделим пункту В 4 ; оставшиеся 6 единиц назначим пункту В 5 , что вместе со всеми 20 единицами пункта А 4 покроет его заявку (табл. 3.2). Таблица 3.2 На этом распределение запасов закончено. Каждый пункт назначения получил согласно своей заявке. Это выражается в том, что сумма перевозок в каждой строке равна запасу, а в столбце – заявку. Таким образом, нами составлен план перевозок, удовлетворяющий балансовым условиям. Полученное решение является не только допустимым, но и опорным решением ТЗ. Клетки таблицы, в которых стоят ненулевые перевозки, являются базисными, их число удовлетворяет условию r = n + m – 1 = 8. Остальные клетки -- свободные, в них стоят нулевые перевозки, их число равно (n – 1)(m – 1) = 12.Значит, составленный план -- опорный и поставленная задача построения опорного плана решена. Но является ли этот план оптимальным? Нет, так как при его совершенно не учитывались стоимости перевозок с i j . И даже, если мы стоимость этого плана перевозок 18 10 + 27 8 + 3 5 + 30 8 + 9 10 + 12 8 + 6 7 + 20 8 = 1039 гарантировать, что этот план оптимальный еще нельзя. Ниже мы рассмотрим способы улучшения плана с целью получения оптимального. Пример 2. Особенности построения «вырожденного плана» План, в котором некоторые из базисных перевозок оказываются равными нулю, называют «вырожденным» Дана транспортная таблица (табл.3.3) Построить опорный план. Решение.
Применяя метод северо-западного угла, получим таблицу 3.3. Опорный план составлен. Особенностью его является то, что в нем только шесть, а не восемь отличных от нуля перевозок. Значит, некоторые из базисных перевозок, которых должно быть быть m + n -- 1 = 8, оказались равными нулю. Отчего это произошло? При распределении запасов по пунктам назначения в некоторых случаях остатки оказывались равными нулю и в соответствующую клетку не попадали. Такие случаи «вырождения « могут возникать не только при составлении опорного плана, но и при его преобразовании, оптимизации. В дальнейшем нам удобно будет всегда в транспортной таблице m + n -- 1 базисных клеток, хотя в некоторых из них, может быть, будут стоять и нулевые значения перевозок. Для этого можно ничтожно мало изменить запасы или Таблица 3,3 Таблица 3.4 Таблица 3.5 заявки, так чтобы общий баланс не нарушился, а лишние «промежуточные» балансы уничтожались. Достаточно в нужных местах изменить запасы или заявки, например, на величину ε , а после нахождения оптимального решения положить ε = 0. Как перейти от вырожденного плана к невырожденному можно понять на примере таблиц 3.4 и 3.5. Изменим слегка запасы в первой строке и положим их равными 20 + ε . Кроме того, в третьей строке проставим запасы 25 + ε. Чтобы «свести баланс» , в четвертой строке ставим запасы 20 -- 2 ε (табл. 3,5). Для этой таблицы строим опорный план методом северо-западного угла. В табл. 3,5 уже содержится столько базисных переменных, сколько требуется: m + n -- 1 = 8. В дальнейшем после оптимизации плана, можно будет положить Метод минимального элемента
позволяет построить начальный опорный план транспортной задачи и является вариантом метода северо-западного угла, учитывающего специфику матрицы С = c i j . В отличие от метода северо-западного угла данный метод позволяет сразу получит достаточно экономичный план, сокращая количество итераций. Смысл метода заключается в том, что элементы матрицы С нумеруют, начиная от минимального в порядке их возрастания, затем в этом же порядке заполняют матрицу Х. Другими словами сначала удовлетворяют заявки, используя самые дешевые перевозки, а затем по мере возрастания их стоимости. Cтраница 1 Опорный план, отвечающий рассматриваемому базису, оптимален, если все AV неотрицательны.
Опорный план будет невырожденным, если он содержит т положительных компонент, в противном случае опорный план называется вырожденным.
Опорный план территории поселения - картографическое отображение фактически сложившейся градостроительной и экологической ситуаций на территории поселения.
Получив первый опорный план, следует проверить его оптимальность и, если требуется, перейти к новому опорному плану с лучшим значением целевой функции Z. Для этого применяют метод потенциалов.
Пусть теперь первый опорный план найден. Существует ряд методов проверки координат вершины на оптимальность.
Находят опорный план расширенной задачи.
Базисом опорного плана будем называть произвольную линейно независимую систему из т столбцов матрицы А, включающую в себя все столбцы, соответствующие ненулевым координатам опорного плана.
Базисом опорного плана называется произвольная линейно независимая система из т столбцов матрицы А, включающая в себя все столбцы, соответствующие ненулевым координатам опорного плана.
По данному опорному плану каждому пункту (производителю или потребителю) сопоставляется число, наз. Предварит, потенциалы определяются из условия: разность предварит, потенциалов нары пунктов (производитель, потребитель) равна стоимости перевозки (СП) единицы продукта между этими пунктами, если связывающая их коммуникация является основной. Далее, для каждой пары пунктов (производитель и потребитель) вычисляется относит, стоимость перевозки единицы продукта, равная разности предварит, потенциалов этих пунктов. Если относит, стоимость перевозки не превосходит СП для любой пары пунктов, то имеющийся план оптимален, а предварит, потенциалы являются потенциалами задачи. Соединим / - и пункт-производитель с i - м пунктом-потребителем обходным маршрутом, составленным из осн.
По данному опорному плану каждому пункту (производителю или потребителю) сопоставляется число, паз. Предварит, потенциалы определяются из условия: разность предварит, потенциалов нары пунктов (производитель, потребитель) равна стоимости перевозки (СП) единицы продукта между этими пунктами, если связывающая их коммуникация является основной. Далее, для каждой пары пунктов (производитель и потребитель) вычисляется относит, стоимость перевозки единицы продукта, равная разности предварит, потенциалов этих пунктов. СП для любой пары пунктов, то имеющийся план оптимален, а предварит, потенциалы являются потенциалами задачи. Пусть это условие не выполняется для нек-рых пар пунктов, одна из к-рых содержит пункты с номерами / и i. Соединим / - и пункт-производитель с i - м пунктом-потребителем обходным маршрутом, составленным из оси.
С новым опорным планом повторяется та же процедура, что и с предыдущим. Один из этих случаев обязательно наступит через конечное число шагов.
Когда в опорный план вводится новая переменная, то для сохранения его базпсности из него должна быть исключена одна из базисных неременных. Таким образом, на каждой итерации симплексного метода новая дуга вводится в план, а одна из базисных дуг исключается. После изменения плана он проверяется на соблюдение условий оптимальности с помощью расчетов, равноценных проверке выполнения всех неравенств (2) при текущих значениях двойственных неременных.