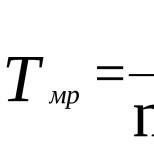Априорная оценка значимости объектов. Априорная и апостериорная оценка качества прогноза
Априорная оценка точности измеряемых навигационных параметров основана на многочисленных статистических исследованиях, которые происходили до конкретной обсервации. В качестве основного параметра для априорной оценки точности измеряемых величин применяется средняя квадратическая погрешность измеряемого навигационного параметра т.
Особенностью определения координат является тот Аакт, что измерения -косвенные, т.е. измеряются навигационные параметры и допущенные погрешности затем переносятся в погрешности координат. Рассмотрим процедуру переноса погрешностей измерений в погрешности координат на примере ОМС по двум измерениям.
В этом случае линеаризованная система принимает вид: ;
Так как измерения имеют погрешности, то перепишем систему в виде
Формирование ковариационной матрицы погрешности измерений выполняется по формуле
![]()
где D - обозначение ковариационной.
Для двумерного случая выражение (2.24) выглядит так:
а операция математического ожидания, выполненная с матрицей 8U6U , превращает ее в ковариационную матрицу D,
![]()
На главной диагонали D находятся дисперсии.измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.
Аналогично определим ковариационную матрицу погрешностей искомых параметров, используя правила матричного исчисления (ABY l =B~ \ A~ \ и (Д- 1)-^^)- 1 .
N = D(A^) = D(SXSX 7) = D^A-"SU^A^SUY] = (A"D^A)^. (2.25)
В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент при D.
Для двумерного случая ковариационная матрица N имеет вид:
где п 11 - дисперсия погрешностей широты, n-г.г - дисперсия погрешностей отшест-вия, ni2 = пг\ - ковариационные моменты.
Вся информация о погрешностях содержится в матрице N. В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим - связь между элементами матрицы N и параметрами эллипса:
полуосями и углом ориентации.
В общем случае такая задача рассматривалась Г. Хоттелингом в 1933 г. Ученым было доказано, что для ковариационной матрицы существуют. векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гиперэллипса для /7-мерного пространства), необходимо извлечь квадратный корень.
Рассмотрим эту задачу для двумерного случая, т.е. для плоскости. Физика и геометрия собственных чисел и векторов заключается в том, что результатом
умножения исходной матрицы на собственный вектор будет вектор, коллинеарный собственному, по длине отличающийся в число раз, пропорциональное собственному значению. Математически это запишется в виде:
Поставим численный эксперимент, который прояснит эту запись. Выполним умножение Nz, где в качестве z будем выбирать единичный вектор с направлением У от 0 до 360°. Формирование компонент единичного вектора
Компоненты вектора р (значения Х и У) приведены в табл. 2.1.
Таблица 2.1
| У | ^1 | Y | X | R |
| 8,13 | 21,000 | 3,000 | 21,213 | |
| 8,48 | 21,049 | 3,139 | 21,282 | |
| 8,83 | 21,092 | 3,277 | 21,345 | |
| 9,18 | 21,128 | 3,415 | 21,402 | |
| 9,53 | 21,158 | 3,551 | 21,454 | |
| 9,87 | 21,182 | 3,686 | 21,500 | |
| 10,22 | 21,199 | 3,820 | 21,540 | |
| 10,55 | 21,209 | 3,953 | 21,574 | |
| 10,90 | 21,213 | 4,084 | 21,603 | |
| 11,24 | 21,211 | 4,215 | 21,625 | |
| 11,58 | 21,202 | 4,344 | 21,642 | |
| 11,92 | 21,187 | 4,471 | 21,653 | |
| 12,26 | 21,165 | 4,598 | 21,658 | |
| 12,60 | 21,137 | 4,723 | 21,658 | |
| 12,93 | 21,102 | 4,846 | 21,651 | |
| 13,27 | 21,061 | 4,968 | 21,639 | |
| ... | ... | ... | ... | |
| 95,38 | -0,692 | 7,358 | 7,390 | |
| 98,30 | -1,062 | 7,281 | 7,358 | |
| 101,24 | -1,432 | 7,201 | 7,342 | |
| 104,19 | -1,801 | 7,120 | 7,344 | |
| 107,13 | -2,169 | 7,037 | 7,363 | |
| 110,05 | -2,537 | 6,951 | 7,400 | |
| 112,94 | -2,905 | 6,863 | 7,453 | |
| 115,72 | -3,271 | 6,113 | 7,522 |
В графе «У» указано направление единичного вектора z, в графе «Ti» -направление уже преобразованного вектора р. В графе «R» приведены значения длины вектора р. Из табличных данных видно, что расхождение в направлении вектора z и вектора р - величина переменная, но в районе 12° и 102° эти направления совпадают. Кроме того, им соответствуют максимальное и минимальное значение длины R. Таким образом, направления собственных векторов 12° и 102° - ортогональны. Собственные значения равны приблизительно 21,658 и 7,342 соответственно.
Для двумерного случая можно получить простые формулы. Согласно выражению (2.26), запишем:
![]()
![]()
а также представим в матричном виде:
Формально получаем

Квадратное уравнение. Решая его относительно X и,
принимая во внимание, что п-ц = пц (т.к. матрица N симметрическая), получим

Подставив значения из матрицы (2.27), получим а] == 21,659; Л^ = 7,341. Эти значения практически совпали с максимальным и минимальным значениями, приведенными в табл. 2.1.
Определим ориентацию собственных векторов, соответствующих найденным собственным значениям. Считая ^ известным, подставим это значение в уравнения системы (2.28) и решим ее относительно zi и z:, учитывая, что z/ == cosfF), z-г = = sinCF).
Первое уравнение системы (2.28) будет выглядеть так:
Разделив в первом уравнении левую и правую часть на cos(T), получим:
 |

Подставив числовые значения, получим ^F = 12,388.
Таким образом, фактически получено направление большой полуоси эллипса У относительно норда. Если в уравнение (2.31) подставить другое значение Л, то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.
Для отыскания полуосей необходимо извлечь квадратные корни из собственных чисел
![]()
Когда говорят об оценке точности, то обычно добавляют слова априорная или апостериорная. Априорная - это оценка точности, выполненная по информации о погрешностях измерений, полученной ранее. Как правило, такая информация о точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации в каких-либо осредненных условиях. Именно такая информация обычно содержится в ковариационной матрице погрешностей измерений, используемой при расчете координат. В формуле (2.18) она обозначена как D. Если погрешности измерений статистически независимы, то внедиагональные элементы равны нулю и матрица имеет вид:

Эти погрешности, в соответствии с правилом их переноса, формируют априорную ковариационную матрицу определяемых параметров.
Процедура построения эллипса погрешностей по ковариационной матрице сводится к следующим операциям:
Расчету собственных значений ^ по формуле (2.29);
Определению угла ориентации У по формуле (2.31);
Расчету полуоси по формулам (2.32).
На рис. 2.5 показана связь между элементами ковариационной матрицы и эллипсом. Отрезок, заключенный между касательной к эллипсу параллельной оси Y и самой осью, соответствует
| СКП по широте: |
Отрезок на оси Y,
отсекаемый вертикальной касательной, соответствует СКП по отшествию:
На рис. 2.5 также показана СКП обсервации М, которая рассчитывается как корень квадратный из следа ковариационной матрицы либо с помощью полуосей эллипса.
Апостериори – на основании опыта.
Априори – независимо от предшествующего опыта.
Оценка качества прогноза – одна из центральных проблем в процессе разработки управленческих решений. Степень доверия к разработанному прогнозу во многом влияет на принимаемое решение и сказывается на эффективности управленческих решений, принимаемых с использованием разработанного прогноза.
Однако, как это ни кажется неожиданным, оценка качества прогноза является достаточно сложной задачей не только в момент, когда прогноз только разработан (априорная оценка), но и в момент, когда прогнозируемое событие уже произошло (апостериорная оценка). Прежде чем приступить к обсуждению оценки качества прогноза, отметим тот важный для более четкого понимания процесса принятия решения факт, что качественный прогноз при принятии решения может быть использован по-разному. Если со стороны руководства организации не оказывается значительное воздействие на ход развития событий, а лишь осуществляется наблюдение за ним, то после окончания прогнозируемого периода не-обходимо лишь сопоставить значения спрогнозированных показателей и параметров с полученными в действительности. Это позволяет оценить качество разработанного прогноза апостериорно.
В то же время, пожалуй, более действенным может оказаться использование результатов разработанного прогноза в случае, когда ЛПР может оказать влияние на ход развития событий. Примером такого влияния может являться, в частности, корректировка управляющих воздействий на основании ожидаемых спрогнозированных значений показателей и параметров. Это так называемый активный прогноз. Однако если в результате анализа спрогнозированных значений показателей и параметров ЛПР изменил управляющие воздействия, которые, в свою очередь, изменили развитие прогнозируемых событий, причем нередко в сторону более благоприятную для ЛПР, то вряд ли корректно первоначально разработанный прогноз считать неточным.
Если бы прогноз не был разработан, то не было бы принято и последовавшее за его разработкой эффективное управленческое решение.
После того как прогноз разработан, должны быть определены критерии, по которым точность прогноза может быть оценена.
Как правило, для оценки прогноза используются два метода: дифференциальный или интегральный.
При дифференциальном методе оцениваются наборы оценок отдельных составляющих качества прогноза, имеющих достаточно четкий объективный смысл.
В частности, могут использоваться такие критерии, как ясность и четкость задания на прогноз, соответствие прогноза заданию, своевременность разработки прогноза, профессиональный уровень разработки прогноза, надежность использованной информации и т. д.
Интегральный метод предполагает обобщенную оценку качества прогноза на базе оценки качества прогноза по частным критериям.
Однако в ряде случаев этот способ оказывается недостаточно убедительным, поскольку к оценке качества прогноза по частным критериям вольно или невольно добавляется необходимость оценки сравнительной важности критериев и их влияния на интегральную оценку.
Примером использования интегрального метода может служить критерий «интегрального качества экспертного прогноза» – оценка прогноза, по которому предполагает, в частности, и оценку по перечисленным выше частным критериям.
Если говорить об экспертном прогнозе, то его качество определяется, прежде всего, такими частными критериями, как:
– компетентность (или в более общем виде – качество) эксперта;
– качество информации, предоставляемой экспертам;
– качество экспертной информации, поступающей от экспертов;
– уровень технологии разработки прогноза или, иными словами, качество методов и процедур, используемых при разработке прогноза.
Если период прогнозирования уже завершился, то необходимо сопоставить спрогнозированные значения показателей и параметров с полученными в результате реализовавшегося с действительности хода прогнозируемых событий.
Для проведения такой оценки необходимо принять во внимание все основные факторы, определяющие качество разработанного прогноза.
7. Контроль хода реализации и корректировки прогноза . После того как прогноз подготовлен и представлен руководству организации, заказчику и т. д., наступает новый этап работы с подготовленным материалом.
Вариантная разработка прогноза также предполагает разработку прогноза при различных альтернативных вариантах условий и предположений, которые могут изменяться. События, вчера казавшиеся маловероятными, сегодня происходят, а казавшиеся наиболее вероятными не происходят вовсе. Базируясь на устаревшем, не учитывающем реалии действительного развития событий прогнозе, трудно принять эффективное управленческое решение.
Поэтому неотъемлемой частью современной технологии прогнозирования является периодически осуществляемый (в зависимости от происходящих изменений) мониторинг хода реализации прогнозированного развития событий.
Мониторинг позволяет своевременно выявлять значительные отклонения в ходе развития событий.
Если они могут оказать принципиальное влияние на дальнейший ход событий в части, касающейся принятия важных стратегических решений, то прогноз должен быть подвергнут корректировке.
Необходимо отчетливо понимать, что прогнозы ценны не сами по себе, как возможность профессионального предсказания ожидаемого хода развития событий в той или иной области человеческой деятельности, а в большей степени как необходимый и очень существенный элемент разработки важных управленческих решений.
Поэтому при выявившихся значительных отклонениях в ходе развития событий в прогнозируемой области деятельности, особенно в случае активного прогноза, в уже разработанный прогноз должны вноситься соответствующие коррективы.
Коррективы могут быть различного уровня значимости, сложности, трудоемкости и т. д. Если они не очень значительны, то эта проблема может решаться на уровне аналитической группы, сопровождающей разработкой прогноза.
Если коррективы более существенны, то может потребоваться дополнительное привлечение отдельных экспертов, а в особо важных случаях при наличии значительных изменений – дополнительная работа экспертной комиссии с возможным изменением состава.
Структура прогноза обусловлена сроками, на которые он рассчитан, а также основными направлениями научно-технического развития, которые прежде всего зависят от «срока жизни» тенденций, сложившихся в пери-од, предшествующих их разработке. Чем более устойчивый характер носят эти тенденции, тем шире может быть горизонт прогнозирования. Различные воспроизводственные процессы имеют разные скорости протекания, разные временные циклы. Цикл воспроизводства приборов значительно короче цикла производства станков и другого оборудования, сроки обновления продукции машиностроения в значительной мере определяются динамикой технического уровня орудий труда.
Прогноз является предплановым документом и поэтому его внедрение на практике означает разработку научно-обоснованной стратегии фирмы, бизнес-план на основе использования вариантов прогноза показателей качества, затрат на его достижение и другой информации.
Прогнозирование управленческих решений преследует цель получения научно-обоснованных альтернатив развития для различных показателей, которые используются в НИОКР, а также для развития всей системы менеджмента. Получается, что прогнозирование управленческих решений есть часть системы менеджмента и способствует развитию всей системы в целом.
Но ЛПР должен помнить, что только решения и планы бывают идеальными, а люди и обстоятельства всегда реальны, и поэтому каждое управленческое решение, каждый план несет в себе возможность не только успеха, но и неудачи.
1. Дайте определения понятиям «прогноз» и «прогнозирование».
2. Какие источники неопределенности выделяют при прогнозировании УР?
3. Каковы основные задачи прогнозирования УР?
4. Какие выделяют источники информации при прогнозировании УР?
5. Охарактеризуйте методы и принципы прогнозирования УР.
6. Какие выделяют этапы прогнозирования УР?
7. Дайте характеристику этапам прогнозирования УР.
Для выполнения данной лабораторно-практической работы проектирование плановой геодезической сети следует выполнять в следующей последовательности:
на теле оползня запроектировать 3 – 4 деформационных знака;
в непосредственной близости от оползневого массива запроектировать 3 – 4 опорных пункта, которые должны быть расположены на устойчивом геологическом основании;
исходные, деформационные и опорные пункты связать в единую геодезическую сеть произвольной конструкции.
Отметим, что при проектировании видимость между пунктами должна быть обеспечена с земли. Сеть может быть запроектирована в виде: триангуляции, трилатерации, линейно-угловой сети, полигонометрии или их комбинаций, при этом специальных допусков на минимальные углы в треугольниках и длины сторон нет. Следует, однако, отметить, что при неудачном проекте сети может оказаться очень высокая необходимая точность угловых или линейных измерений, что приведет к удорожанию работ.
Общее число определяемых пунктов в геодезической сети (в учебных целях ) должна находиться в диапазоне 6n’8. Число избыточных измеренийrв сети, вычисляемое по формуле (5), рекомендуется проектировать в диапазоне 5r10. Приr5 возможен неудовлетворительный результат предрасчета точности, а приr10 – необоснованное удорожание стоимости запроектированной геодезической сети.
где n– число всех измерений в сети;
t– число параметров (для плановой сети число параметров равно удвоенному числу определяемых пунктов ).
Проектирование высотной геодезической сети осуществляется по пунктам плановой сети в виде хода или системы нивелирных ходов с одной или несколькими узловыми реперами.
2 Априорная оценка точности геодезических сетей
2.1 Общие теоретические положения
Оценка точности геодезических сетей выполняется как на стадии проектирования, когда разрабатывается оптимальный вариант построения сети, так и после построения сети в процессе математической обработки (уравнивания ) результатов геодезических измерений.
Оценка точности, выполняемая по результатам уравнивания, дает наиболее достоверные данные о реальной точности элементов построенной на местности геодезической сети. Эта информация используется при решении различных научных и практических задач, требующих определения с заданной точностью длин и направлений сторон сети, координат и высот геодезических пунктов.
Особое значение оценка точности геодезических сетей имеет на стадии проектирования. Благодаря ей представляется возможность решать целый ряд задач, имеющих большое практическое и экономическое значение, и в частности:
выбор оптимального варианта построения сети, позволяющего при прочих равных условиях получить элементы сети с наивысшей точностью, достигаемой в массовых работах при наименьших затратах труда, денежных средств и времени на их производство;
определить требуемую точность измерения элементов в проектируемой сети и на их основе сделать правильный выбор приборов и методов измерений.
В настоящее время априорную оценку точности геодезических сетей выполняют на персональных компьютерах по методу наименьших квадратов с учетом всех геометрических и корреляционных связей между уравненными элементами сети. Для оценки точности необходимо получить матрицу весовых коэффициентов определяемых пунктов по следующей известной формуле
 (6)
(6)
где А - матрица параметрических уравнений поправок;
Р - матрица весов результатов измерений.
Число строк в матрице А определяется числом всех измерений в сети (n), а число столбцов - удвоенным числом определяемых пунктов. Строка матрицы А представляет собой коэффициенты параметрического уравнения поправок для соответствующего измерения.
Для измеренных углов параметрическое уравнение поправок в индексном виде записывается следующим образом
где k" - порядковый номер измеренного угла в сети;
k, i, j - индексы, соответствующие номерам пунктов, образующих проектируемый измеренный угол;
 - поправки к приближенным значениям
координат определяемых пунктов (на
стадии предвычисления точности они
остаются неизвестными и обозначают
соответствующие столбцы матрицы
параметрических уравнений поправок
А
);
- поправки к приближенным значениям
координат определяемых пунктов (на
стадии предвычисления точности они
остаются неизвестными и обозначают
соответствующие столбцы матрицы
параметрических уравнений поправок
А
);
 - коэффициенты параметрического уравнения
поправок, вычисляемые по следующим
формулам
- коэффициенты параметрического уравнения
поправок, вычисляемые по следующим
формулам
где
 - соответственно дирекционный угол и
длина линии Skj.
- соответственно дирекционный угол и
длина линии Skj.
Для запроектированных измеренных расстояний, параметрическое уравнение поправок в индексном виде записывается следующим образом
Диагональные элементы матрицы Р - веса соответствующих измерений. Для запроектированных измеренных углов они вычисляются по следующей формуле
 (10)
(10)
где - средняя квадратическая ошибка (СКО) единицы веса; M- СКО измеренного угла.
На стадии предвычисления точности, как правило, принимают условие =m , поэтому веса измеренных углов в формуле (10) равны 1.
Веса измеренных расстояний с учетом принятого условия (10) определяются по формуле
Отметим, что на диагонали матрицы Р для проектируемых измеренных длин линий находится неизвестное соотношение между точностями проектируемых угловых и линейных измерений, поскольку заранее класс геодезической сети не определен. Следовательно, для решения матричного уравнения (6) априорно установим вес линейного измерения в виде произвольного положительного числа К, которое, в частном случае, может быть равно 1. Правила составления матрицы коэффициентов параметрических уравнений поправок А и матрицы весов результатов измерений Р подробно изложены в работе /13 /.
Средняя квадратическая ошибка положения произвольного пункта в сети относительно ближайшего исходного пункта может быть вычислена по формуле
где Q Xi иQ Yi – соответствующие диагональные элементы матрицы весовых коэффициентов определяемых параметровQ,
- средняя квадратическая ошибка единицы веса.
На стадии проектирования геодезической сети ошибку единицы веса считают известной из имеющегося опыта построения сетей. Она, как правило, приравнивается к СКО измеренных углов=m и устанавливается в соответствующей нормативной литературе /8/ исходя из класса геодезической сети. Для геодезической сети, предназначенной для наблюдения за движением оползня, задана точность положения пункта в наиболее слабом месте, а класс геодезического построения не определен /4/. Следовательно, формулу (12) целесообразно преобразовать к следующему виду
 (13)
(13)
Формула (8) позволяет, исходя из заданной точности положения пункта в наиболее слабом месте геодезической сети вычислить требуемую точность угловых измерений. В соответствии с условием (10) формула для вычисления необходимой точности запроектированных измеряемых длин линий вычисляется по следующей формуле
 (14)
(14)
Таким образом, для выполнения априорной оценки точности запроектированных наблюдений в геодезической сети, предназначенной для наблюдения за движением оползня, сети необходимо выполнить следующие этапы математической обработки:
по формулам (7 и 9 ) составить параметрические уравнения поправок для всех проектируемых измерений;
вычислить коэффициенты уравнений поправок по формулам (8);
установить веса запроектированных измерений (матрица Р, формулы 10 и 11 );
по формуле (6) вычислить матрицу весовых коэффициентов Q;
вычислить требуемую точность угловых и линейных измерений по формулам (13 и 14).
Априорная оценка точности высотных геодезических сетей выполняется аналогичным образом на основании матрицы весовых коэффициентов, вычисляемой по формуле (6 ). Для высотных геодезических сетей в уравнении (6)матрица параметрических уравнений поправок А составляется на основании следующего выражения
Следовательно, коэффициенты параметрического уравнения поправок могут быть равны +1 или -1. Число строк в матрице А равно числу всех измерений, а число столбцов (в отличии от плановых сетей ) - числу определяемых реперов.
Веса запроектированных измерений в высотных сетях вычисляются исходя из следующей формулы
 (16)
(16)
где L i - j – длина секции нивелирного хода между определяемыми реперамиiиj(размерность км. );S i - j – длина линии между определяемыми реперами, измеренная с топографической карты; К – коэффициент, который изменяется в пределах 1.1К1.3 и зависит от рельефа местности. .
Средняя квадратическая ошибка определения репера в сети геометрического нивелирования может быть вычислена по следующей известной формуле
 (17)
(17)
где - СКО единицы веса, которая на стадии предвычисления точности, принимается равной СКО на 1 км.хода. Она соответствует нормативным требованиям, которые определяются по запроектированному классу геометрического нивелирования;
Q Hi – диагональный элемент матрицы весовых коэффициентов.
Учитывая, что для высотной геодезической сети задается нормативная точность определения репера в наиболее слабом месте сети преобразуем формулу (17 ) к следующему виду
 (18)
(18)
Оценка качества эксперта может быть:
1) априорной – если в ней не используется информация о его участии в других экспертизах (т.е. эксперт оценивается априорно, до того, как он был использован в качестве эксперта) ;
2) апостериорной – если она использует такую информацию (основана на ней) и
3) тестовой – в форме специального тестового испытания, направленного на выявление необходимых качеств эксперта.
К априорным методам оценки относятся:
1) самооценка эксперта. Она может осуществляться
а) с использованием балльной шкалы (например, 5-балльной) ;
б) с использованием других шкал. Например, если необходимо отнести себя к одной из двух групп - «теоретик» или «практик», - то речь идет о самооценке в номинальной шкале (шкале наименований), на которой задано только отношение тождества (либо объект относится к некоторой группе, либо нет). Если необходимо отнести себя к одной из групп: «начинающий исследователь», «исследователь, имеющий опыт работы в данной области», «исследователь с большим опытом работы», «углубленный специалист по исследованиям в данной области», - то речь идет об ординальной шкале (шкале порядков), на которой задано отношение «больше-меньше» («лучше-хуже»). Она может быть дополнена указанием некоторых числовых диапазонов, например, если специалист занимается данной областью исследований менее полугода, его считают начинающим, от полугода до 2 лет – имеющим опыт, от 2 до 5 лет – большой опыт, более 5 – углубленно знакомым с предметом. Более подробно типы шкал будут рассмотрены далее ;
в) путем расчета интегральных (агрегированных) показателей самооценки по различным показателям (например, по уровню знакомства с различными источниками информации в определенной области специалист оценивает себя 5 баллами, а по уровню знакомства с исследуемой проблемой – 4-мя баллами по 5-балльной шкале; если веса этих показателей равны соответственно 0.8 и 0.2, то агрегированная оценка составит 5*0.8 + 4*0.2 = 4.8). Подробнее способ расчета агрегированных показателей был рассмотрен при изучении принципа оптимальности;
Недостатком всех методов самооценки является то, что такая оценка тесно связана с уровнем самокритичности, что затрудняет ее интерпретацию. Достоинством является простота получения такой оценки.
2) взаимная оценка экспертов. Здесь, в свою очередь, потенциальным членам экспертной группы могут быть предложены различные методы оценки друг друга – балльные оценки, сравнительные оценки, простое формирование списков и т.п. (подробнее рассматривается далее). Полученные от разных экспертов оценки подлежат дальнейшей обработке для получения отдельной оценки для каждого эксперта. Т.е. такая оценка, в свою очередь, является групповой экспертной оценкой, и встает проблема ее обработки для получения общей оценки (см. далее). Такая оценка предположительно является более объективной, чем самооценка, но
Процесс ее получения более сложен;
- кроме того, здесь также могут проявиться личностные и групповые симпатии и антипатии, что повлияет на объективность;
- и, наконец, различные эксперты по одному и тому же вопросу не обязательно хорошо знакомы с работами и возможностями друг друга. В современных условиях такое знакомство может быть лишь у специалистов, длительно работающих совместно. Однако их одновременное привлечение к экспертизе может быть не целесообразно, поскольку они слишком похожи друг на друга.
3) документационный метод (так называемый метод объективных оценок, или метод формальных показателей) – основан на использовании соответствующим образом заверенных документов, содержащих объективную информацию об эксперте (диплом, трудовая книжка и т.п.). Например, для вхождения в экспертную группу могут быть предъявлены следующие требования: стаж работы не менее трех лет (подтверждается выпиской из трудовой книжки), высшее образование (подтверждается дипломом), не менее 10 научных трудов (подтверждается списком, заверенным соответствующим лицом). Объективность оценки, полученной по данному методу, зависит от добросовестности и объективности суждений лиц, выдающих и заверяющих используемые документы, а также репутации соответствующих организаций (например, дипломы разных вузов объективно имеют различную ценность, стаж работы в различных организациях также неравноценен и т.п.). Рекомендуется использовать данный метод только как вспомогательный.
4) и прочие методы.
Априорная оценка точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации. В качестве основного параметра для априорной оценки точности измеряемых величин применяется средняя квадратическая погрешность измеряемого навигационного параметра m .
Особенностью определения координат является тот факт, что измерения косвенные, то есть измеряются навигационные параметры, и их погрешности затем переносятся в погрешности координат. Рассмотрим процедуру переноса погрешностей измерений в погрешности координат на примере ОМС по двум измерениям.
В этом случае линеаризованная система принимает вид:
Так как в измерениях присутствуют погрешности , то это приведет к погрешности вектора оценок и система перепишется в виде:
Формирование ковариационной матрицы погрешности измерений выполняется по формуле
здесь D – обозначение ковариационной матрицы или, что тоже самое,символ дисперсии вектора вектора .
Для двумерного случая умножение выглядит так:
а операция математического ожидания, выполненная над матрицей превращает ее в ковариационную матрицу D :
![]() .
.
На главной диагонали D находятся дисперсии измеряемых навигационных параметров, а вне диагонали - ковариационные моменты, которые характеризуют статистическую связь между измерениями.
Аналогично определим ковариационную матрицу погрешностей определяемых параметров, используя правила матричного исчисления ![]() и
и ![]() ,
,
В дальнейшем при написании ковариационных матриц, где это не вносит двузначности, будем опускать аргумент при D .
И так, ковариационная матрица погрешностей координат N рассчитывается так:
Для двумерного случая матрица N имеет вид:
где n 11 - дисперсия погрешностей широты, n 22 - дисперсия погрешностей отшествия, n 12 = n 21 - ковариационные моменты.
Вся информация о погрешностях содержится в матрице N . В судовождении часто используется ее геометрическая интерпретация в виде эллипса погрешностей. Установим связь между элементами матрицы N и параметрами эллипса: полуосями и углом ориентации.
В общем случае такая задача рассматривалась Хоттелингом Г. в 1933 г. и им было показано, что для ковариационной матрицы существуют векторы, направлениям которых соответствуют максимальные и минимальные значения рассеивания (погрешностей). Численно эти значения соответствуют собственным числам матрицы. Направления собственных векторов, указывающие на направление максимального и минимального рассеивания (дисперсии), соответствуют направлениям полуосей эллипса. Собственные числа - это экстремальные значения дисперсий. Для перехода к линейным величинам - полуосям эллипса (гипер - эллипса для n-мерного пространства), необходимо извлечь квадратный корень.
Рассмотрим эту задачу для двумерного случая, то есть для плоскости. Физика и геометрия собственных чисел и векторов заключается в том, что результатом умножения исходной матрицы на собственный вектор будет вектор, коллинеарный собственному, по длине отличаясь в число раз, пропорциональное собственному значению. Математически это запишется так:
Поставим численный эксперимент, который прояснит этот факт.
Выполним умножение Nz , где в качестве z будем выбирать единичный вектор с направлением Y от 0 0 до 360 0 . Формирование компонент единичного вектора выполним по формулам:

В качестве примера возьмем матрицу
В результате перемножения конец вектора p опишет эллипс. (Рис.2.4)
Процедуру умножения матрицы N на z можно рассматривать как оператор, преобразующий единичный вектор z . После перемножения вектор изменит направление и длину. Ниже приведены результаты такого перемножения с дискретностью в один градус, а компоненты вектора p (значения x и y ), приведены в таблице 2.1
| Y | Y 1 | x | y | R |
| 8.13 | 21.000 | 3.000 | 21.213 | |
| 8.48 | 21.049 | 3.139 | 21.282 | |
| 8.83 | 21.092 | 3.277 | 21.345 | |
| 9.18 | 21.128 | 3.415 | 21.402 | |
| 9.53 | 21.158 | 3.551 | 21.454 | |
| 9.87 | 21.182 | 3.686 | 21.500 | |
| 10.22 | 21.199 | 3.820 | 21.540 | |
| 10.55 | 21.209 | 3.953 | 21.574 | |
| 10.90 | 21.213 | 4.084 | 21.603 | |
| 11.24 | 21.211 | 4.215 | 21.625 | |
| 11.58 | 21.202 | 4.344 | 21.642 | |
| 11.92 | 21.187 | 4.471 | 21.653 | |
| 12.26 | 21.165 | 4.598 | 21.658 | |
| 12.60 | 21.137 | 4.723 | 21.658 | |
| 12.93 | 21.102 | 4.846 | 21.651 | |
| 13.27 | 21.061 | 4.968 | 21.639 | |
| … | … | … | … | … |
| 92,48 | -0,322 | 7,432 | 7,439 | |
| 95,38 | -0,692 | 7,358 | 7,390 | |
| 98,30 | -1,062 | 7,281 | 7,358 | |
| 101,24 | -1,432 | 7,201 | 7,342 | |
| 104,19 | -1,801 | 7,120 | 7,344 | |
| 107,13 | -2,169 | 7,037 | 7,363 | |
| 110,05 | -2,537 | 6,951 | 7,400 | |
| 112,94 | -2,905 | 6,863 | 7,453 | |
| 115,78 | -3,271 | 6,773 | 7,522 | |
| … | … | … | … |
В первом столбце таблицы находится направление единичного вектора z , а во втором, направление уже преобразованного вектора - вектора p . В последнем столбце содержится длина R вектора p . Из расчетов, приведенных в таблице видно, что расхождение в направлении вектора z и вектора p величина переменная, но в районе 12 0 и 102 0 эти направления совпадают. Кроме того, этим направлениям соответствуют максимальное и минимальное значение длины R . Таким образом, направления собственных векторов 12 0 и 102 0 соответственно, они ортогональны. Собственные значения равны приблизительно 21.658 и 7.342 соответственно.
Для двумерного случая можно получить простые формулы для расчета параметров эллипса погрешностей из матрицы N . Опираясь на выражение (2.26), запишем.
n 11 z 1 + n 12 z 2 = lz 1
n 21 z 1 + n 22 z 2 = lz 2 (2.28).
(n 11 -l)z 1 + n 12 z 2 =0
n 21 z 1 + (n 22 -l)z 2 =0
или в матричном виде:
(N - lE) z = 0
где - нулевая матрица.
Формально получаем:
![]()
Det(N-lE)Z=adj(N-lE)*0
следовательно, Det(N-lE)Z= 0 .
Так как Z произвольный вектор и, в общем случае не нулевой, то
Det(N-lE)=0
Запишем для двумерного случая:
![]()
(n 11 - l) (n 22 - l) - n 21 n 12 = 0
Это квадратное уравнение. Решая его относительно l и, принимая во внимание, что n 21 = n 12 , так как матрица N симметрическая, получим:
![]() (2.29)
(2.29)
Подставив значения из матрицы (2.27), получим l 1 = 21.659 l 2 = 7.341
Эти значения практически совпали с максимальным и минимальным значением из таблицы.
Определим ориентацию собственных векторов, соответствующих найденным собственным значениям. Считая l известным, подставим это значение в (2.28) и разрешим эту систему относительно z 1 и z 2 ,учитывая, что z 1 = cos(Y), z 2 = sin(Y) .
Первое уравнение системы 2.28 будет выглядеть так:
n 11 cos(Y) + n 12 sin(Y) = l cos(Y)
Разделим первое левую и правую часть на cos(Y).
n 11 + n 12 tg(Y) = l
![]() . (2.30)
. (2.30)
![]() (2.31).
(2.31).
Подставив числовые значения, получим Y = 12.388 0
 Таким образом, фактически получено направление большой полуоси эллипса Y
относительно норда. Если в (2.31) подставить другое значение l
то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.
Таким образом, фактически получено направление большой полуоси эллипса Y
относительно норда. Если в (2.31) подставить другое значение l
то получим направление малой полуоси, но так как они ортогональны, то практически это не требуется.
Для отыскания полуосей необходимо извлечь квадратные корни из собственных чисел.
Когда говорят об оценке точности, то обычно добавляют слова априорная или апостериорная. Априорная - это оценка точности, выполненная по информации о погрешностях измерений полученной ранее. Как правило, такая информация о точности измеряемых навигационных параметров основывается на многочисленных статистических исследованиях, которые происходили до конкретной обсервации в каких-то осредненных условиях. Именно такая информация, как правило, содержится в ковариационной матрице погрешностей измерений используемой при расчете координат. В формуле (2.18) она обозначена как D . Если погрешности измерений статистически независимы, то внедиагональные элементы равны нулю и матрица имеет вид:

Именно эти погрешности в соответствии с правилом переноса погрешностей и формируют априорную ковариационную матрицу определяемых параметров.
Процедура построения эллипса погрешностей по ковариационной матрице сводится к следующему:
· Рассчитываем собственные значения l по формуле (2.29)
· Определяем угол ориентации Y по формуле (2.31)
· Рассчитываем полуоси по (2.32)
На рис. 2.5 показана связь между элементами ковариационной матрицы и эллипсом. Отрезок, заключенный между касательной к эллипсу параллельной оси Y и самой осью соответствует СКП по широте, или Отрезок на оси Y , отсекаемый вертикальной касательной соответствует СКП по отшествию
На рисунке также показана средняя квадратическая погрешность (СКП) обсервации М, которая рассчитывается, как корень квадратный из следа ковариационной матрицы либо с помощью полуосей эллипса:
2.5 Апостериорная оценка точности рассчитанных координат
В априорной оценке использовалась информация о точности, полученная по результатам предыдущих измерений, а в апостериорной оценке участвуют текущие измерения, т.е. по которым была вычислена вероятнейшая точка.
Допустим, что ковариационная матрица погрешностей измерений D известна с точностью до постоянного множителя m 2:
где матрица K известна, а величина m 2 неизвестна.
Иными словами известны относительные, а не абсолютные значения матрицы D . С учетом этого рассмотрим систему нормальных уравнений:
Подставив вместо D -1 выражение получим:
![]()
Величина m 2 (дисперсия наблюдения с единичным весом) сокращается и решение, в итоге, не зависит от абсолютной величины элементов ковариационной матрицы измерений D . Матрицу K -1 также называют "весовой" и обозначают через P ,а m 2 - дисперсией наблюдения с единичным весом. Если m 2 не выносилась из D , то весовой будет просто D -1 .
Рассмотрим величину
Она представляет собой обобщенную (взвешенную) остаточную сумму квадратов уклонений. Здесь M - операция взятия математического ожидания. Упрощенно ее можно рассматривать как отыскание среднего значения.
Рассмотрим выражение в последней скобке, то есть пока без операции взятия математического ожидания:
Последнее слагаемое равно 0. Это вытекает из условия (2.17) и видно из рисунка 2.6: векторы и ортогональны, а скалярное произведение таких векторов равно 0. Тогда .
 |
Кроме этого:
Во втором слагаемом произведение представляет собой правую часть системы нормальных уравнений (2.19), тогда вместо нее запишем левую , тогда окончательно получим:
По этой формуле можно посчитать значение квадратичного критерия (остаточную сумму квадратов невязок). Здесь DU - вектор, рассчитанный по исходным данным U o -U c и первое слагаемое в правой части дает значение остаточной суммы в начальной (счислимой) точке, а второе слагаемое уменьшает это значение за счет смещения к оптимальной точке на величину .
С учетом взятия операции математического ожидания (2.33) справедливо следующее:
Распишем первое слагаемое:
Правило легко проверяется простым перемножением матриц небольшой размерности.
Распишем второе слагаемое:
С учетом (2.35) получим:
![]()
Несмещенная оценка m 2 запишется выражением:
Тогда апостериорную оценку ковариационной матрицы погрешности результатов получим следующим
или апостериорная ковариационная матрица погрешностей координат рассчитывается через априорную матрицу так:
Пример . Определить координаты места судна и поправку компаса по измерениям 4-х пеленгов. Расчитать элементы априорного и апостериорного эллипсов погрешностей координат, и средние квадратические погрешности обсервации.
Задачу решить на плоскости в прямоугольных координатах по информации представленной ниже,используя два последовательных приближения.
Окончательный ответ дать в географической системе координат.
Счислимые координаты: x = 8,0 (миль) ; ,y = 4,4 (миль)
Решение:
Первая итерация:
1. Записываем навигационную функцию пеленга ()с учетом поправки Z:
![]()
 Вычисления приведены ниже:
Вычисления приведены ниже:
| |

Затем из априорной ковариационной матрицы N выбираем верхний левый блок N 1 , который определяет точность координат x,y и по формулам (2.26)-(2.29), находим элементы априорного эллипса погрешностей обсервации и СКП М
Элементы априорного эллипса погрешностей обсервации из N’:
a =98,6 м; b =35,6 м; y=139,4 0 ; М=104,82 м
Элементы апостериорного эллипса погрешностей обсервации из вернего левого блока матрицы (2.36):
a =149,3 м; b =53,9 м; y=139,4 0 ; М=149.30 м
Вторая итерация:
1. Обсервованные коородинаты принимаем за счислимые, т.е. X c = , и повторяем вычисления по формулам (2.20) и (2.26)-(2.29) с расчетом оценки точности координат.
2. С учетом принятых обозначений, а именно ![]() , определяем географические координаты, при известных географических координатах счислимой точки С
(j с, l с):
, определяем географические координаты, при известных географических координатах счислимой точки С
(j с, l с):
l о =l с + cos j m , где j m = (j с + j о)/2 – средняя широта.
2.6 Графоаналитический расчет

Где М ij – средняя квадратическая погрешность точки по двум линиям положения.
- Находим средневзвешенное значения приращений координат относительно счислимой точки:

- Находим обсервованные прямоугольные координаты, используя формулы (2.8), а так же географические координаты по формулам, приведенным во второй итерации.
- Для сравнения ставим точку по первой итерации на диаграмму графоаналитического расчета.
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12